5.3. Мінімальна кон’юнктивна нормальна форма

Мінімальна кон’юнктивна нормальна форма (МКНФ) записується як кон’юнкція елементарних диз’юнкцій , що відповідають виділеним блокам нулів на карті Карно.

Для отримання МКНФ необхідно виконати такі дії:

• заносимо нульові значення функції в карту Карно;

• створюємо ПК за нульовими значеннями. Нулі, які ввійшли на попередніх кроках в одну із диз’юнкцій, вважаємо покритими. Із непокритих і покритих нулів створюємо наступну диз’юнкцію, покриваючи максимальну кількість непокритих нулів. Нову диз’юнкцію тільки із покритих нулів створювати не потрібно. Процес завершується тоді, коли покриті всі нулі;

• описуємо всі ПК за допомогою таблиці;

• для кожної ПК складаємо диз’юнкцію змінних, від яких вона залежить.

Якщо змінна для даної ПК приймає нульове значення, то вона береться в прямому вигляді, а інакше – в інверсному:

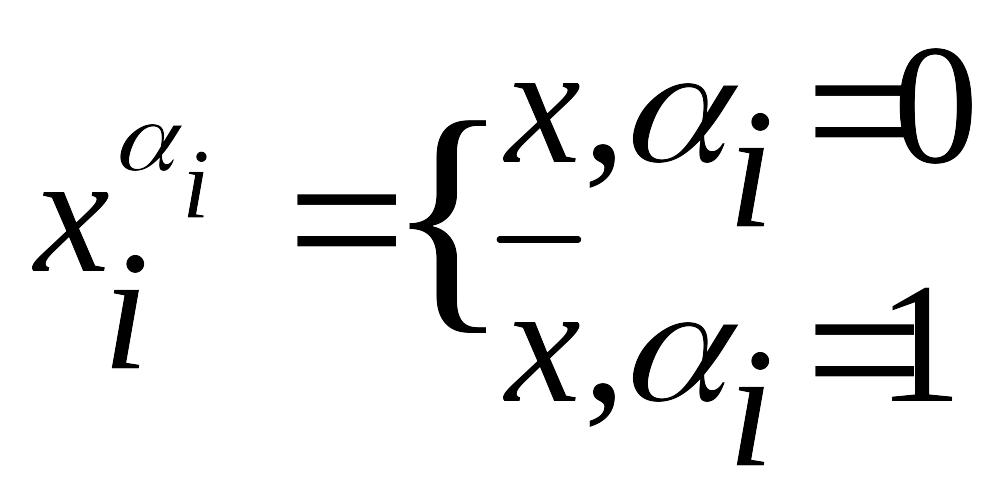
• об’єднуємо за допомогою операції кон’юнкції всі описані ПК:

(5.2)

й отримуємо мінімальну кон’юнктивну нормальну форму.

Приклад 4. Функція f₄ задана таблицею істинності (табл.5.9). Побудувати МКНФ.

Таблиця 5.9 – Таблиця істинності функції f₄

х1	х2	х3	f4
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

Заносимо нульові значення функції f₄ в карту Карно.

ПК₁¹

х ₁ ПК₂¹

х2	6	7	0 3	0 2
	4	0 5	1	0 0

ПК₃⁰ х₃

Об’єднуємо клітинки 2 і 3 в ПК₁¹ , клітинки 0 і 2 – в ПК₂¹, а клітинку 5 – в ПК₃⁰. Правильні конфігурації описуємо за допомогою табл. 5.10.

Таблиця 5.10 – Опис значень змінних для правильних конфігурацій за нульовими значеннями функції f₄

Правильні конфігурації	Значення змінних
	х1	х2	x3
ПК11	0	1	–
ПК21	0	–	0
ПК30	1	0	1

ПК₁¹ описується як диз’юнкція змінних . ПК₂¹ описується як диз’юнкція змінних . ПК₃⁰ описується як диз’юнкція змінних . Об’єднавши за допомогою операції кон’юнкції одержані описи ПК, отримаємо МКНФ:

f_4мкнф = ( ) ( ) ( ).