4.1. Досконала диз’юнктивна нормальна форма

Оскільки між множиною аналітичного подавання і множиною схем, які реалізують булеву функцію, існує взаємно однозначна відповідність, відшукування канонічної форми подання булевої функції є початковим етапом синтезу схеми, що її реалізує. Найбільше поширення отримала досконала диз’юнктивна нормальна форма (ДДНФ). Наведемо визначення конституенти одиниці – поняття, яке буде далі широко використовуватись.

Визначення. Конституентою одиниці називається функція f (x₁, x₂, …, x_n), яка приймає значення 1 тільки на одному наборі.

Конституента одиниці записується у вигляді терма, тобто у вигляді логічного множення п різних булевих змінних, деякі з яких можуть бути з використанням заперечення. Наприклад, f = – елементарний логічний добуток, який являється конституентою одиниці змінних x₁, x₂, x₃ і x₄, приймає значення 1 тільки на одному наборі 1001. Зрозуміло, що на решті 15 наборах ця функція приймає значення 0.

Якщо згадати, що диз’юнкція приймає значення 1, коли хоча б одна зі змінних приймає значення 1, то можна легко виразити будь-яку булеву функцію як диз’юнкцію конституент одиниці, які відповідають тим наборам, на яких функція приймає значення 1. У більш загальному вигляді це можна записати таким чином (4.1):

,

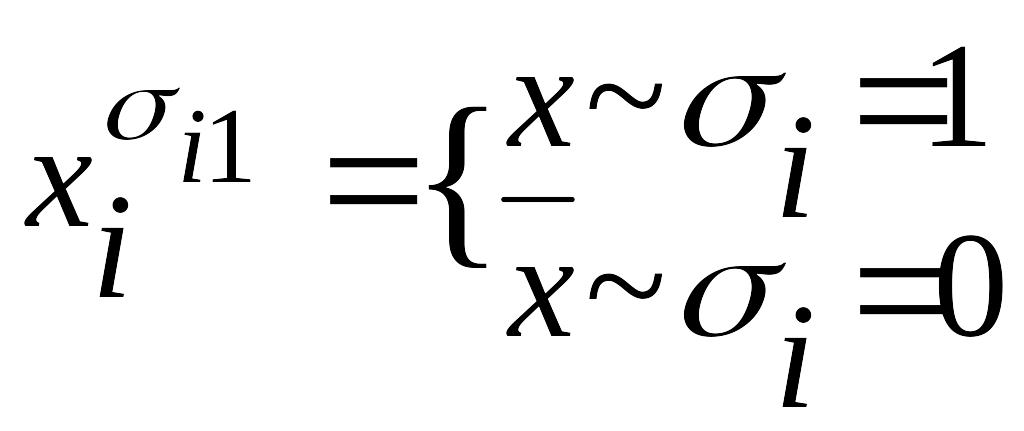де і . (4.1)

Ц

Таблиця 4.1 – Таблиця істинності

x1	x 2	x3	f1	f2
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

я форма і є ДДНФ. Відмітимо, що набори, на яких функція f приймає значення 1, часто називаються одиничними, а інші – нульовими наборами. Виписувати в ДДНФ доцільно тільки конституенти одиниці, тобто те, що відповідає одиничним наборам. Подання булевої функції в ДДНФ єдине.

Приклад 1. Випишемо ДДНФ для функцій, заданих таблицею істинності (табл. 4.1).

.

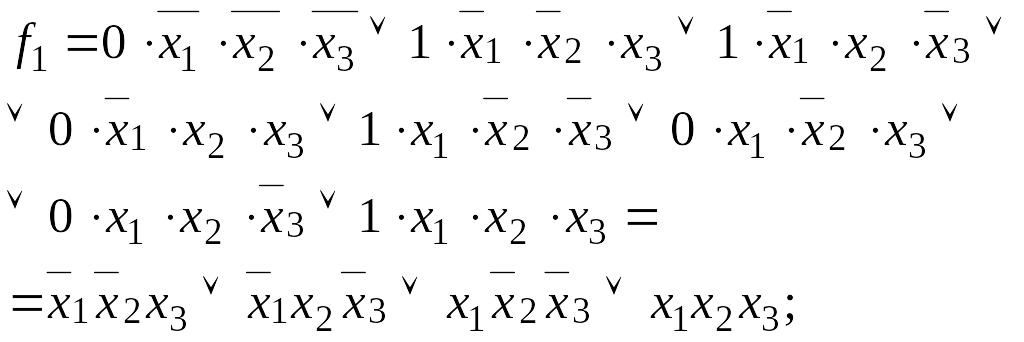
4.2. Досконала кон’юнктивна нормальна форма

Друга відома форма носить назву досконалої кон’юнктивної нормальної форми (ДКНФ). Вона будується аналогічно ДДНФ, але при цьому використовуються конституенти нуля.

Визначення. Конституентою нуля називається функція, яка приймає значення 0 тільки на одному наборі.

Конституента нуля записується у вигляді елементарної диз’юнкції всіх змінних даної функції. Кожному набору відповідає своя конституента нуля. Наприклад, набору 0110 змінних х₁, х_2, x₃ і x₄ відповідає конституента нуля . ДКНФ представляється як кон’юнкція конституент нуля, які відповідають тим наборам, на яких функція приймає значення 0. У більш загальному вигляді це можна записати таким чином (4.2):

,

де і 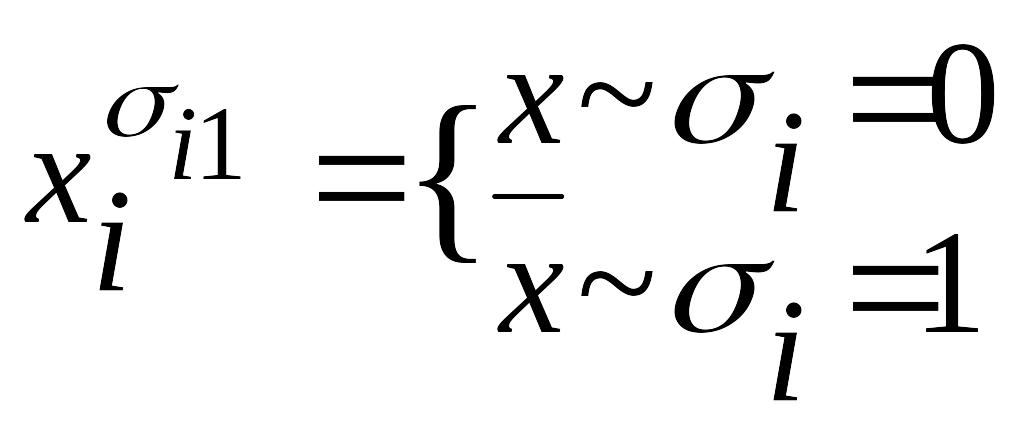. (4.2)

Приклад 2. Для розглянутої вище функції f₁ (див. табл. 4.1) побудуємо ДКНФ

.