2.9. Нечітка логіка. Загальні поняття

Часто потрібно приймати рішення при неповному, нечіткому або неясному описі об'єктів або зв'язків між ними. Наприклад, «великий вхідний опір осцилографа», «постійне число обертів двигуна» не дають числової характеристики атрибута об'єкта, або «судно стоїть біля причалу», «літак знаходиться в аеропорту» не дають числової оцінки зв'язків між об'єктами, або «якщо йде дощ, то закриті всі люки», «якщо температура тіла 38 С, то людина хвора» дають лише якісний опис логіки рішень.

Неповний опис елемента або ситуації не дозволяє оцінити міру їх приналежності до певного класу і з упевненістю дати оцінку правильності рішення.

Для подібних задач розроблена нечітка логіка (fuzzi logic), об'єктом дослідження якої є нечіткі множини (fuzzi set), нечіткі відношення (fuzzi relation), нечіткі операції алгебри і нечітке числення (fuzzi calculus).

Звичайна «чітка» множина має чіткі межі в деякому універсумі. Приналежність елемента універсуму до деякої множини оцінюється бінарно: «Так» чи «Ні». Така приналежність елемента х до множини А на універсумі U може бути описана функцією приналежності _А

А = {(х, _А(х))}, х  U, _А(х)  {0,1}.

Тут А задано як сукупність пар – «елемент – степінь приналежності до множини», тобто для звичайної множини _А – це відображення елементів універсуму U в бінарну множину {0, 1}:_А:U {0, 1}.

Нечітка множина А в універсумі (просторі) U задається функцією приналежності, що відображає універсум не в бінарну множину, а в інтервал [0,1]. Тоді задання нечіткої множини виглядає так:

А = {(х, _А(х))}, х  U, _А(х)  [0,1], :_А:U [0, 1],

тобто степінь приналежності елемента до множини оцінюється не стрибком «або 0, або 1», а плавно, наприклад: 0; 0,1; 0,4; 0,7; 0,9; 1. Функція приналежності може задаватися формулою або графічно (наприклад так, як вказано на рис. 2.4).

Р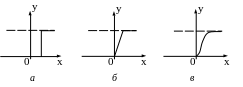 исунок 2.4 – Функції приналежності:

а – дискретна; б – плавно-кусково-лінійна; в – сигмоїда

У випадку кінцевої осяжної множини застосовують такий запис:

.

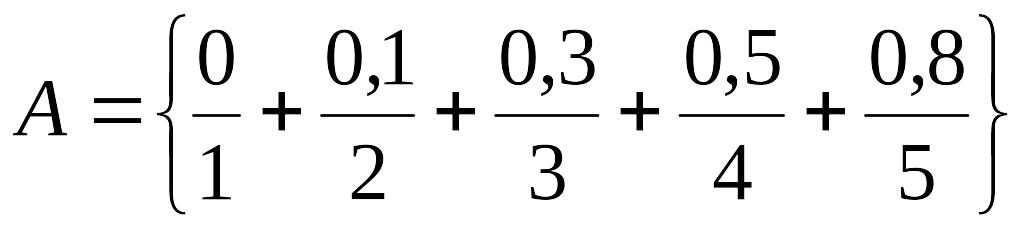Це означає, що:

• елемент 1 належить до універсуму U зі степенем 0, тобто не належить;

• елемент 2 належить до універсуму U зі степенем 0,1;

• елемент 3 належить до універсуму U зі степенем 0,3;

• елемент 4 належить до універсуму U зі степенем 0,5;

• елемент 5 належить до універсуму U зі степенем 0,8.

Знак + означає об'єднання елементів. Сам універсум U = 1 + 2 + 3 + 4 + 5.

Множина порожня, якщо x  U _А(х) = 0, тобто А = .

Якщо x  U _А(х) = 1, то А = U.

Дві множини А і В рівні, якщо _А = _В, тобто А = В.

Множина А включається у В, якщо _А ≤ _В, тобто А  В.

Множина є доповненням множини А, якщо _А = 1 – _А.

Вводяться також двомісні теоретико-множинні операції.

Приклад 20. Нехай дано 10 дискет. Множина всіх підмножин цих дискет містить порожню множину, одно-, дво- три- і так далі до десятиелементної підмножини. Так, задано універсальну множину U = {, 1, 2, 3, ..., 10}. На цій множині необхідно вибрати підмножини, що задовольняють поняттю «Вибрати декілька дискет».

Для підмножин, що містять нуль, один, два, половину або всі дискети, експерт визначив значення функції приналежності рівним нулю, оскільки можна було б сказати конкретно: «взяти половину дискет», «взяти дві дискети» і тому подібне Для підмножин, що містять три, вісім або дев'ять дискет, експерт визначив значення функції приналежності рівним 0,6, а для підмножин, що містять чотири, шість або сім дискет, – рівним 0,8.

Отже, експерт виконав поставлене завдання так:

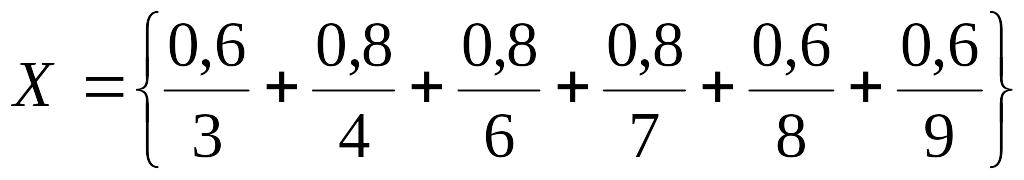
Носієм цієї нечіткої підмножини є X = {3, 4, 6, 7, 8, 9}.

Така була суб'єктивна міра приналежності кожної підмножини універсальної множини нечіткому поняттю «Узяти декілька дискет».