2.4. Застосування алгебри логіки в теорії автоматів. Схеми перемикачів

Як одну з інтерпретацій булевих функцій розглянемо електричну схему, що складається з джерела напруги (батареї), лампочки і одного або двох ключів (x₁ і x₂). Ключі управляються кнопками з двома станами: кнопка натиснута (1) і кнопка відпущена (0). Якщо у вихідному стані ключ розімкнений, то при натисненні кнопки він замикається. Ключ може бути сконструйований і так, що в вихідному стані він замкнутий, тоді натиснення кнопки означає його розмикання, тобто приводить до протилежного результату. Тому нормально замкнуті ключі позначимо через і .

При відповідних станах кнопок лампочка приймає один з двох станів: горить (1) і не горить (0). Стани кнопок ототожнюються зі значеннями булевих змінних х₁ та х₂, а стан лампочки – зі значенням функцій цих змінних.

Операції заперечення відповідає схема з одним нормально замкнутим ключем (рис. 2.1, а). Якщо кнопка натиснута (х = 1), ключ розімкнений і лампочка не горить, тобто f(x) = 0; при відпущеній кнопці (х = 0) ключ замкнутий і лампочка горить, тобто f(x) = 1. Операціям диз'юнкції і кон'юнкції відповідають схеми з двома нормально розімкненими ключами (рис. 2.1, б, в).

а

б

в

Рисунок 2.1 – Схеми перемикачів, відповідні операціям

заперечення (а), диз'юнкції (б) і кон'юнкції (в)

Легко переконатися, що в схемі рис. 2.1, б лампочка горить при натисненні хоч би однієї з кнопок, а в схемі рис. 2.1, в – тільки при натисненні обох кнопок одночасно.

Будь-яку складну булеву функцію можна представити деякою схемою перемикача. На рис. 2.2, а показана схема, що реалізує функцію . Та ж функція представляється рівносильною формулою , якій відповідає інша простіша схема (рис. 2.2, б). Слід мати на увазі, що ключі, позначені однаковими буквами (х або ), зв'язані між собою і управляються загальною кнопкою.

а б

Рисунок 2.2 – Схема перемикача, що реалізує логічну функцію (а), та спрощена схема (б)

У реальних пристроях використовуються ключі різної конструкції і фізичної природи (механічні, електромагнітні, електронні, гідравлічні, пневматичні і так далі). Проте при реалізації логічних функцій багато технічних особливостей не мають значення. Істотними властивостями контактних схем є початкові положення ключів (нормально розімкнені або нормально замкнуті) та спосіб їх з'єднання між собою і зовнішніми пристроями. Ця інформація повністю відображається графом, ребра якого відповідають ключам, а вершини – точкам їх з'єднання. Ребра нормально розімкнених ключів позначаються відповідною змінною (х), а нормально замкнутих – запереченням змінної . 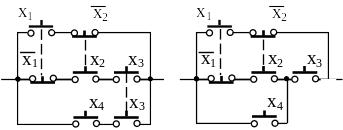Наприклад, контактна схема (рис. 2.2, б) зображається графом, як показано на рис. 2.3, а.

а б

Рисунок 2.3 – Граф схеми перемикача (а)

та його спрощене зображення (б)

При зображенні контактних схем графами приймаються деякі специфічні умови і спрощення. Зазвичай змінні позначаються в розривах ліній, що зображають ребра. При цьому ребрами вважаються тільки такі лінії, які позначені якою-небудь змінною або її запереченням. Інші лінії, що не є ребрами графа, можуть зображати входи і виходи схеми, зв'язки з іншими схемами і тому подібне. Крім того, вершини другого степеня можуть не зображатися, оскільки їм інцидентні пари послідовно з'єднаних ребер, з яких кожне позначене відповідною змінною. На рис. 2.3, б показана контактна схема у загальноприйнятому вигляді.