34 Корригирование зубчатых колёс

При нарезании колёс режущий инструмент можно располагать ближе к заготовке или дальше от неё. Положение инструмента определяется расстоянием между делительной окружностью колеса и так называемой модульной прямой рейки, проходящей через середину высоты зуба режущего инструмента (рис.78).

  

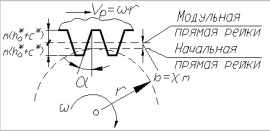
В зависимости   от  положения рейки по делительной окружности может перекатываться без скольжения либо модульная прямая рейки, либо начальная прямая, отстоящая от модульной прямой на величину смещения “b”, которое называется сдвигом или  коррекцией, а коэффициент χ (хи), равный χ=b/m, называется коэффициентом смещения инструмента. Если инструмент смещён от нарезаемого колеса, то χ считается положительным (положительная коррекция), а если – к центру колеса, то χ отрицателен (отрицательная коррекция). При χ=0 нарезаемое колесо называется нормальным (нулевым). Толщина зуба и ширина впадины такого колеса по делительной окружности равны.

При положительной коррекции увеличивается прочность зуба, но уменьшается длина линии зацепления, а следовательно и коэффициент  перекрытия . При отрицательной коррекции – обратный эффект, т. е. увеличивается плавность и бесшумность работы передачи, но прочность зуба уменьшается.

Зацепление двух зубчатых колёс характеризуется суммарным коэффициентом коррекции χ_Σ=χ₁+χ₂, причём возможны три случая:

1) χ_Σ=0 при χ₁=χ₂=0, когда в зацеплении находятся два нулевых зубчатых колеса (нулевое зацепление);

2) χ_Σ=0 при χ₁=-χ₂, когда в зацеплении находятся два корригированных зубчатых колеса, коэффициенты коррекции которых равны по величине и противоположны по знаку (равносмещённое зацепление с высотной коррекцией);

3) χ_Σ≠0, когда в зацеплении находятся два корригированных колеса, имеющих:

  а) χ_Σ>0 – положительное неравносмещённое зацепление с угловой коррекцией;

  б) χ_Σ<0 - отрицательное неравносмещённое зацепление с угловой коррекцией.

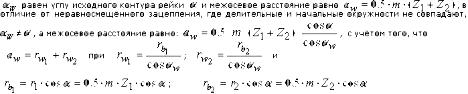
36 Характеристика внешних сил.

Характеристикой внешней силы называется её зависимость от какого-либо кинематического параметра. Например: (см. рис.3.39).

1. Характеристика силы зависит от времени. Это имеет место в механизм перемешивающего аппарата. Сила изменяется, т.к. меняются с течением времени вяз­кие свойства перемешиваемой среды.

2. Характеристика силы зависит от перемещения. Наиболее распространенный случай. Так, сила упругости пружины зависит от величины её деформации S , усилие вытяжки пресса от изменения диаметра заготовки.

3. Характеристика силы зависит от скорости. Случай, характерный для демпфирующих механизмов, греб­ных вёсел и винта и т.д.

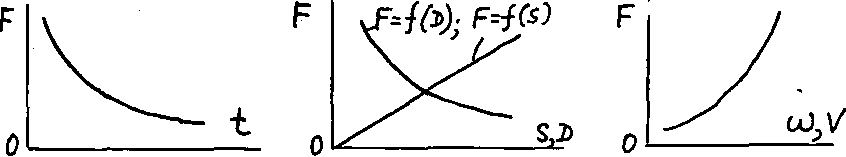
Рис.3.39 Зависимость силы от кинематических параметров.

39 Теорема Жуковского о жестком рычаге

             Одним из способов определения приведенной силы F^пр является способ, предложенный проф. Н.Е. Жуковским. Уравнение, из которого может быть найдена F^пр, основано на равенстве мощностей:   F_∑^пр·V_A·cos(F_∑^пр V_A)=∑F_i·V_i·cos(F_i V_i).

 Рассмотрим какое-либо звено механизма, в т. В которого приложена сила F_i под углом α_i к вектору скорости V_i этой точки (рис.25, а). Мощность силы F_i равна:    

  P_i=F_i·V_i·cosα_i.  Если вектор скорости т. В (план скоростей) повернуть на Рис.25      90^˚ и силу F_i приложить к концу вектора (в т. «b»), сохранив ее направление, то момент этой силы относительно полюса «p» будет равен (рис.25, б):     M_i=F_i·h_i=F_i·V_i·cosα_i=P_i,

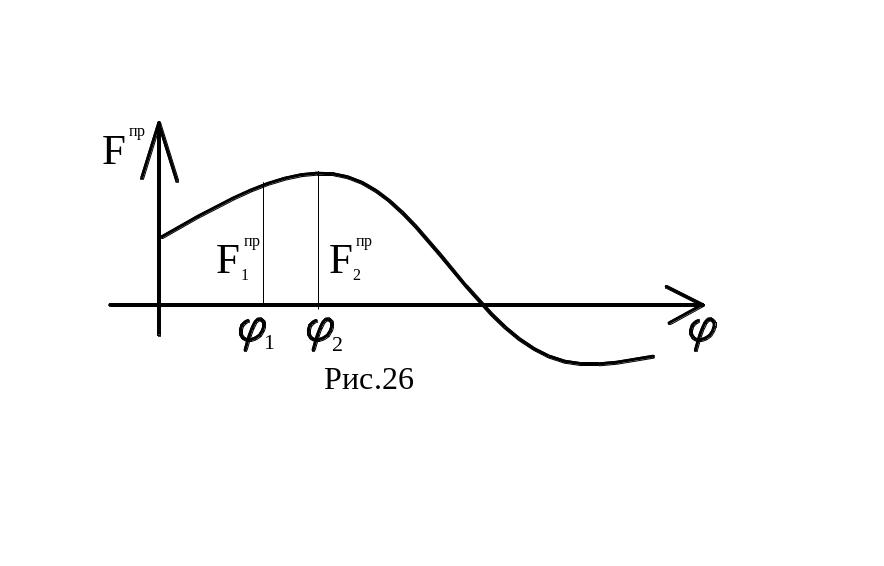
 т.е. равен мощности силы F_i. Таким образом, F_i можно найти, повернув на 90^˚ план скоростей и приложив к нему все внешние силы, включая силы инерции, в соответствующих точках и сохраняя их направления. Тогда из уравнения моментов такого рычага: F_∑^пр·h_пр=∑F_i·h_i,  получим: F_∑^пр=∑F_i·h_i/h_пр, где h_i и h_пр – кратчайшие расстояния от полюса плана скоростей до линии действия i-ой и приведенной сил. Повернутый на 90^˚ план скоростей с приложенными к нему силами называется жестким рычагом Жуковского. Величина F^пр или М^пр зависит от положения механизма, поэтому можно построить диаграмму, например, F^пр(φ), являющуюся функцией положения звена приведения. Для этого необходимо последовательно определить значения F^пр методом рычага Жуковского для целого ряда положений механизма в пределах цикла (F₁^пр, F₂^пр,…) и отложить их на диаграмме (рис.26).

Приведенная сила F∑пр или момент М∑пр характеризует реакцию механизма на движение его входного звена по определенному закону, задаваемому двигателем. Сила или момент, равные по величине приведенной силе или моменту, но противоположные им по направлению называется уравновешенной силой Fур или моментом Мур. Эта сила или момент развивается двигателем и обеспечивает заданное движение входного звена.

Если к рычагу Жуковского приложить все внешние силы, включая силы инерции, а также Fур, то его можно рассматривать в равновесии, из условия которого: Fур•hур+∑Fi•hi=0 можно определить неизвестную Fур, а также найти мощность двигателя Pдв, требуемую для получения заданного движения входного звена в заданном положении:

Pдв=Fур•VA•cos(FурVA)=Mур•ω.

 

40 Кулачковые механизмы: Кулачковым называется трехзвенный механизм с высшей кинематической парой входное звено которого называется кулачком, а выходное - толкателем (или коромыслом). Часто для замены в высшей паре трения скольжения трением качения и уменьшения износа, как кулачка, так и толкателя, в схему механизма включают дополнительное звено - ролик и вращательную кинематическую пару. Подвижность в этой кинематической паре не изменяет передаточных функций механизма и является местной подвижностью.  Назначение и область применения: Кулачковые механизмы предназначены для преобразования вращательного или поступательного движения кулачка в возвратно-вращательное или возвратно-поступательное движение толкателя. При этом в механизме с двумя подвижными звеньями можно реализовать преобразование движения по сложному закону. Важным преимуществом кулачковых механизмов является возможность обеспечения точных выстоев выходного звена. Это преимущество определило их широкое применение в простейших устройствах цикловой автоматики и в механических счетно-решающих устройствах (арифмометры, календарные механизмы). Кулачковые механизмы можно разделить на две группы. Механизмы первой обеспечивают перемещение толкателя по заданному закону движения. Механизмы второй группы обеспечивают только заданное максимальное перемещение выходного звена - ход толкателя. При этом закон, по которому осуществляется это перемещение, выбирается из набора типовых законов движения в зависимости от условий эксплуатации и технологии изготовления.  Классификация кулачковых механизмов: Кулачковые механизмы классифицируются по следующим признакам:

по расположению звеньев в пространстве : пространственные; плоские;

по движению кулачка : вращательное; поступательное; винтовое

по движению выходного звена: возвратно-поступательное ( с толкателем); возвратно-вращательное ( с коромыслом)

по наличию ролика: с роликом; без ролика;

по виду кулачка: дисковый (плоский); цилиндрический; коноид (сложный пространственный);

по форме рабочей поверхности выходного звена: плоская; заостренная; цилиндрическая; сферическая; эвольвентная;

по способу замыкания элементов высшей пары: силовое; геометрическое;

П

ри силовом замыкании удаление толкателя осуществляется воздействием контактной поверхности кулачка на толкатель (ведущее звено - кулачок, ведомое - толкатель). Движение толкателя при сближении осуществляется за счет силы упругости пружины или силы веса толкателя, при этом кулачок не является ведущим звеном. При геометрическом замыкании движение толкателя при удалении осуществляется воздействием наружной рабочей поверхности кулачка на толкатель, при сближении - воздействием внутренней рабочей поверхности кулачка на толкатель. На обеих фазах движения кулачок ведущее звено, толкатель – ведомое

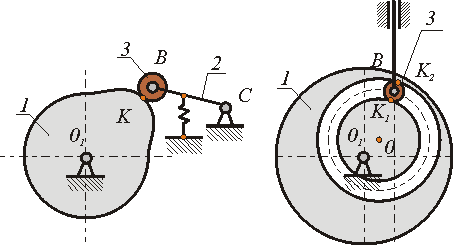
Кулачковый механизм с силовым Кулачковый механизм с геометрическим замыканием высшей пары замыканием высшей пары