1 8 Приведение сил и масс. Динамические модели машины.

Определение закона движения механизма через уравнение (3.39) , в котором кинематические параметры звеньев находятся в определенных соотношения друг с другом, выражаемых через свои уравнения, довольно затруднительно. Для упращения составления уравнения движения механизма и его решения ,достаточно, пользуясь методом приведения сил и масс, установить закон движения его звена или одной точки, т.е. найти только одну неизвестную функцию. Решение этой задачи осуществляется созданием динамической модели машины, в которой модель имеет такой же закон движения как и сама машина.

Для этой модели все силы и моменты сил, действующие на машину, заменяются одной силой или моментом сил называются приведенной силой или приведенной массой. Приведение сил и моментов сил осуществляются либо к точке (если обобщенной координатой является линейная координата ), либо к звену ( если обобщенной координатой является угловая координата ). В качестве точки приведения обычно выбирается точка на ведущем звене, в качестве звена приведения – ведущее звено. Если ведущее звено механизма является кривошипом, то и звено при -ведения имеет такой же вид (кривошип), если ведущее звено – ползун, то звено приведения - ползун. Условим приведения сил и масс является закон сохранения энергии. Т.е. мощность или работа приведенной силы или момента сил должна равняться суммарной мощности или работе всех внешних сил или моментов сил, а кинетическая энергия звена приведения равна суммарной кинетической энергии всех звеньев.

Е сли приведенная сила F_пр , приложенная к точке направлена по касательной к её траектории ,то равенство (3.41) можно записать как

Где, F_i , M_i - сила и момент, приложенные к звену; V_i - скорость точки приложения силы;  - угловая скорость звена.

Если вместо приведенной силы определяется приведенный момент сил,то аналогично равенству (3.43)

Из уравнений (3.43) и (3.44) получим Из условия (3.42) Где для звена приведения - ползун; для звена приведения - кривошип.

Подставляя соответствующие выражения в формулу (3.47) и разрешая её относительно приведенных параметров получим: Как известно величины отношения скоростей (аналоги скоростей) зависят только от положения механизма, будучи одинаковыми при любом законе движения механизма. Поэтому и приведенная сила или приведенный момент сил, приведенная масса или приведенный момент инерции от закона движения не зависят, а зависят от положения его звена приведения.

20 Определение момента инерции маховика методом виттенбауэра

Подбор момента инерции J_м маховика по заданномукоэффициенту неравномерности δ

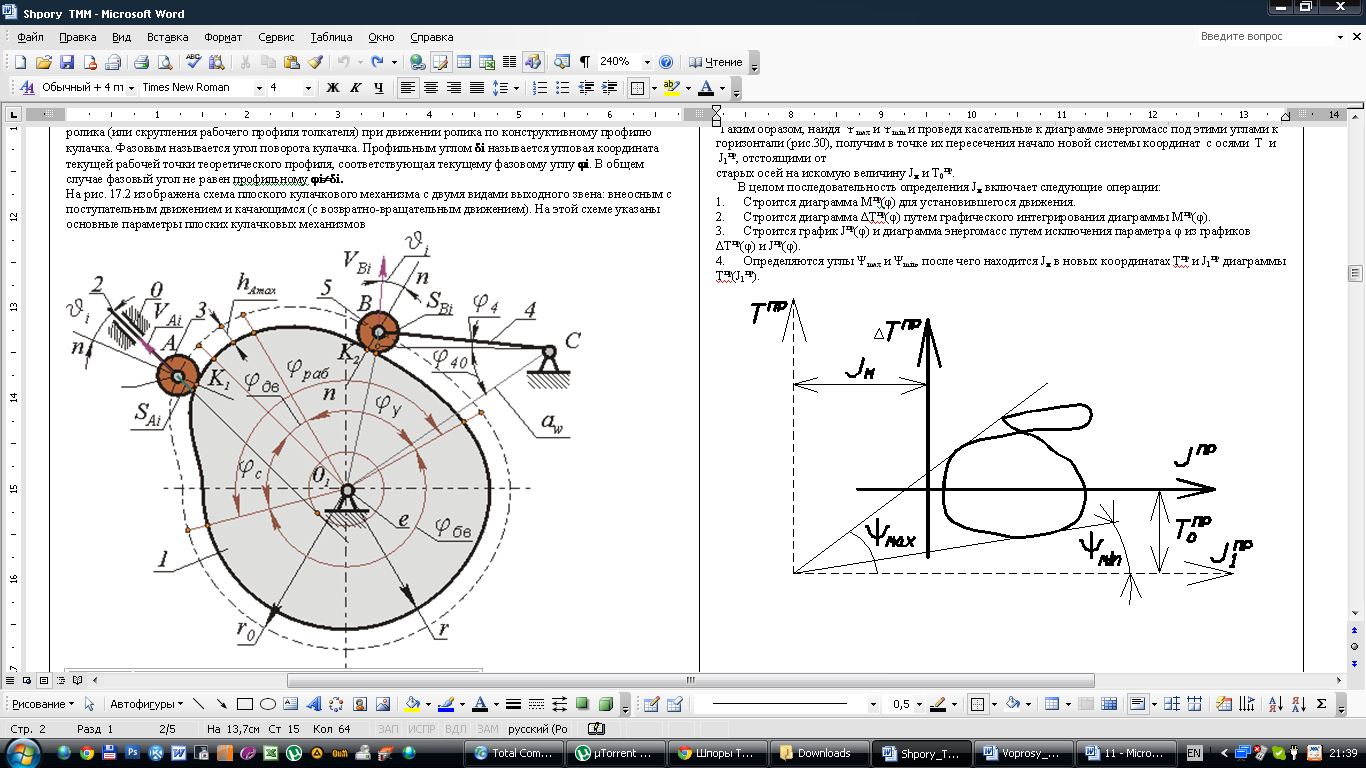
    Обычно требуется определить параметры маховика при заданных значениях ω_ср и δ. Существует два наиболее распространенных метода определения J_м – Н.И. Мерцалова и метод Ф. Виттенбауэра. Рассмотрим более точный метод Ф. Виттенбауэра, при котором предварительно строится диаграмма энергомасс ∆Т^пр(J^пр).                                                                                                                                    

Согласно этой диаграмме (рис.30):   ω²_max,min=2·μ_Т/μ_J·tgΨ_max,min,           

  tgΨ_max,min= μ_J/μ_T·ω²_max,min/2.

 С  другой  стороны  из  урав-нений п.5.6.:                                                 

  ω_max,min=ω_с·(1+(-)δ/2).

 Таким образом, найдя  Ψ_max и Ψ_min и проведя касательные к диаграмме энергомасс под этими углами к горизонтали (рис.30), получим в точке их пересечения начало новой системы координат  с осями  Т  и  J₁^пр, отстоящими от

старых осей на искомую величину J_м и Т₀^пр.

       В целом последовательность определения J_м включает следующие операции:

1.      Строится диаграмма М^пр(φ) для установившегося движения.

2.      Строится диаграмма ∆Т^пр(φ) путем графического интегрирования диаграммы М^пр(φ).

3.      Строится график J^пр(φ) и диаграмма энергомасс путем исключения параметра φ из графиков ∆Т^пр(φ) и J^пр(φ).

4.      Определяются углы Ψ_max и Ψ_min, после чего находится J_м в новых координатах Т^пр и J₁^пр диаграммы Т^пр(J₁^пр).

21) Механические передачи(редукторы,мультипликаторы,коробки скоростей,вариаторы,фрикционные передачи). К сложным зубчатым механизмам относятся также зубчатые коробки передач. Зубчатой коробкой передач называется зубчатый механизм, передаточное отношение которого можно изменять скачкообразно по ступеням. Коробками передач снабжаются те машины, рабочие органы которых должны вращаться с различными скоростями в зависимости от условий работы. Например, обработка различных деталей на токарном станке производится при разных скоростях, поэтому в механизм токарного станка включается коробка передач. Коробки передач применяются в автомобилях для получения различных скоростей движения автомобиля. Схема и конструктивное оформление коробок передач бывают чрезвычайно разнообразными. Если число ступеней регулирования скорости невелико, то схема коробки получается достаточно простой, при большом же числе ступеней регулирования как схема, так и конструктивное оформление могут быть весьма сложными. Коробка передач состоит из зубчатых колес, которые могут быть введены в зацепление в различных комбинациях для получения передаточных отношений, соответствующих заданным скоростям вращения рабочего органа машины. Способы переключения отдельных колес для получения различных передаточных отношений разнообразны, зависят от конструктивного оформления коробки Механизмы, осуществляющие плавное изменение передаточного отношения, называются механизмами бесступенчатых передач или вариаторами скоростей. На рис. 7.6 показан механизм бесступенчатой передачи с двумя дисками 1 и 5 и промежуточным роликом 2. Передаточное отношение U51 между параллельными осями 01 и О5 равно U51=w5/w1=x1/x5 т. е. передаточное отношение не зависит от радиуса ролика 2. Направление вращения осей О1 и О5 одинаковое. Передаточное отношение U51 можно изменять в пределах Х1мин/Х5макс<=U51<=Х1макс/Х5мин Передаточный механизмы, которые понижают скорость на выходе наз. редукторами. Передаточный механизмы, которые увеличивают скорость на выходе наз. мультипликаторами. Изменение числа оборотов может быть ступенчатым и неступенчатым. Механизмы со ступенчатым изменением числа оборотов:коробка скоростей,передач. Механизмы с неступенчатым изменением числа оборотов:вариатор. Механизмы позволяющие изменять на выходном валу направление на противоположное без изменения вращения ведущего звена наз. реверсивными. Если направление вращения на входном и выходном валу совпадают-передача положительная, не совпадают-отрицательные. Знаки плюс и минус-условные. Фрикционные передачи-это передачи движение которых о существляется за счёт сил трениия.