11 Графоаналитический метод кинематического анализа - метод планов скоростей и ускорений.

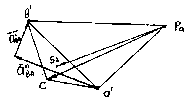
Пусть дан кривошипно - ползунный механизм, схема которого пока­зана на рис. 2.7. Известны длины звеньев, положение механизма и постоянная угловая скорость кривошипа W₁. Требуется определить скорости и ускорения точек А, В, С, и угловые скорость и ускоре­ние шатуна W₂ и E₂.

2.3.1 Построение планов скоростей. Определяем скорость точки А кривошипа по формуле ,Здесь - длина кривошипа ОА в М.

Назначаем полюс плана скоростей Р_V и из него перпендику­лярно кривошипу ОА откладываем отрезок P_V a (рис2.8), представляющий собой вектор скорости точки А при масштабном коэффициенте плана скоростей . который определяется выражением

где P_V a -длина вектора в мм на плане скоростей. Для определения скорости точки В движение шатуна разложим на переносное поступательное со скоростью точки А и относитель­ное вращательное вокруг этой точки. Такое разложение движения описывается векторным уравнением.

В таблицу под уравнением внесены данные о величине и нап­равлении векторов. Неизвестными здесь являются величины векторов.

V_B и V_BA при известных их направлениях. Такое уравнение может быть решено графически построением плана скоростей. Из полюса P_V проводится направление вектора , а из конца вектора скорости точки А - направление вектора . На пересечении этих прямых находится конец вектора скорости точки В (точка "в" плана скоростей). Теперь можно найти скорость любой другой точки. Например, для скорости точки С можно записать два векторных уравнения:

,

Проведя из точек а и в плана скоростей прямые, перпендикулярные отрезки АВ и ВС шатуна найдем конец вектора скорости точки С, начало его лежит в полюсе Р_V. Величины скоростей точек А, В, С в м/с определяются выражениями:

Т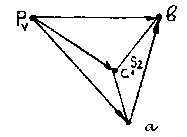 аким образом, если у звена известны величина и направление скорости одной точки и направление скорости (траектория) другой точки, то можно определить скорость любой его точки.

12 Построение планов ускорений.

Определяем ускорение точки А кривошипа по формуле

Здесь , - нормальное и тангенциальная составляющие. В нашем примере , поэтому Нормальное ускорение определяется выражением Этот вектор направлен параллельно ОА к центру вращения кривошипа (от точки А к точке 0 на звене).Назначаем масштабный коэффициент плана ускорений и определяем длину вектора Р_aa который будет представлять ускорение точки А.

Из полюса плана ускорений P_a откладываем отрезок рис. 2.9. Здесь стрелка внизу показывает направление вектора от точки А к точке 0 на звене.Для определения ускорения точки В опять разложим движение шатуна, как при построении плана скоростей. Тогда будем иметь

В этом уравнении и -нормальная и тангенциаль­ная составляющие относительного ускорения . Нормальная состав­ляющая вычисляется по формуле

Здесь ab - отрезок плана скоростей. Начало и конец вектора на плане ускорений обозначим точкамиа и n₂ ; n -говорит, что отложено нормальное ускорение, индекс 2 - что рассматривалось звено 2. Полученное векторное уравнение может быть решено графически построением плана ускорений. Для этого из полюса Р_a проводим направление вектора абсолютного ускорения точки В параллельно направляющим ползуна b и далее строим векторную сумму по правой части уравнения. Пересечение известных по направлению векторов и ,и дает решение - точку "в" плана ускорений. Отрезок n₂b в принятом масштабе представляет вектор , величина которого равна Зная величину и направление тангенциальной составляющей отно­сительного ускорения точек В и А, можно определить величину и направление углового ускорения шатуна . Его величина определяется выражением Для определения направления - вектор показываем выходящим из точки В на звене.