44.2 Порядок силового расчета.

F32y + F34y = 0 .(4.14) Отсюда найдем проекцию F34y. Направление силы , приложенной к ползуну 3 от стойки 4, определяется ее знаком. Осталось неиспользованным уравнение моментов , которое употребим для определения плеча b силы (см. рис. 4.8, а): F34у (xD – xC) = 0,(4.15) откуда получим b = (xD – xC) = 0 и xD = xC. Таким образом, для структурной группы 2–3 были использованы шесть уравнений (4.10) – (4.15), из которых были определены все неизвестные. План сил, приложенных к звеньям структурной группы, представлен на рис. 4.8, б. Этот план наглядно показывает, как важно учитывать влияние ускоренного движения звеньев. Если им пренебречь, т.е. положить силы инерции и равными нулю (рис. 4.8, в), то такой неучет приведет к заниженным значениям сил в кинематических парах (сил , , ), что особенно проявит себя в механизмах быстроходных машин. Перейдем к силовому расчету двухзвенного механизма, составленного из подвижного звена 1 и стойки 4 (рис. 4.9). К звену 1 приложены: ставшая известной сила момент М1, направленный, согласно рис. 4.7, по ходу часовой стрелки, главный момент сил инерции МФ1 и неизвестная по модулю и направлению реакция стойки. Напомним, что главный вектор сил инерции Ф1 = 0.

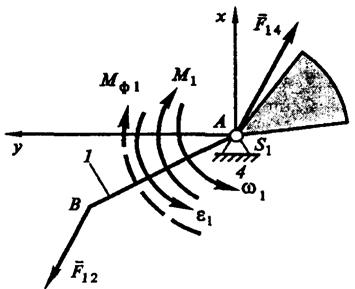Рис. 4.9. Схема двухзвенного механизма для силового расчета Поскольку Ф1 = 0, уравнения проекций сил, приложенных к звену 1, т.е. , , приобретают вид F14x + F12x = 0 ; F14y + F12y = 0 , отсюда F14x = – F12x, F14y = – F12y. Составим уравнение моментов для звена 1 относительно точки А: Момент подставим в уравнение с тем знаком, который он получает при подсчете по формуле Уравнение (4.18) является контрольным, поскольку все три слагаемых в его левой части известны. Однако оно может быть и расчетным, когда момент М1 неизвестен. Заметим, если нужно определить только внешний (уравновешивающий) момент М1и не обязательно определять силы в кинематических парах, то момент М1 можно найти и более коротким путем, не расчленяя механизм, а применив теорему Жуковского. При малой неравномерности вращения звена 1 его угловое ускорение ε1в начале расчета часто не определяют, поскольку оно мало. Однако принять вследствие этого МФ1 =– ε1J1A ≈ 0 нельзя. Неравенство момента МФ1 нулю вытекает из уравнения (4.18), поскольку моменты М1 и заведомо не равны и сильно различаются. Момент МФ1 может иметь значительную величину, что существенно для расчета главного вала машины (звена 1) на прочность.

48 Виды трения.

Общее сопротивление, возникающее в местах соприкоснове- ния двух тел, которые перемещаются друг относительно друга, называется силой трения. Сопротивление движению возникает из-за упругих вязких и пластических деформаций шерохова­тых поверхностей соприкасающихся тел.

Трение в одних случаях является полезным фактором, на- пример: при сцеплении винта и гайки с закрепляемой деталью колес автомобиля или трамвая с дорогой, дисков тормозов различных машин.

В других случаях трение вызывает непроизводительный расход энергии, быстрый износ трущихся деталей. Например, короткий ресурс различных двигателей, редукторов, ряда машин, объясняется быстрым износом контактирующих поверх­ностей звеньев, т. е. кинематических пар.

Уменьшая трение в кинематических парах, можно обеспечить уменьшение расхода энергии и увеличить их долговечность, а следовательно повысить ресурс различных машин.

Трение препятствует относительному движению звеньев в кинематических парах. В зависимости от характера относительного движения различают:

- трение скольжение в низших кинематических парах,

- трение качения или трение качения с трением скольжения в высших кинематических парах.

Трение скольжения, в свою очередь можно разделить на:

- сухое трение (из-за сопротивления микронеровностей контактирующих поверхностей при отсутствии смазки),

- полусухое трение (из-за сопротивления микронеровностей при наличии смазки),

- жидкостное трение (при отсутствии контакта по­верхностей жидким слоем жидкости, за счет вязкости жидкости). Природа сухого и жидкостного трения, а также трения качения - различна, поэтому отличаются и методы определения тех сопротивлений, которые появляются при относительном движении элементов кинематических пар. В технических расчетах для определения силы трения сухих поверхностей пользуются формулой F=f·N, (3.14)

где f - коэффициент трения скольжения при движении

N - нормальная сила Коэффициент трения покоя f₀ больше коэффициента трения при движении, т.e. f₀>f. Коэффициент f зависит от многих факторов и определяется экспериментально; для основных материалов он приводится в справочниках, Зависимостью (3.14) пользуются для оценки силы тре­ния в поступательных кинематических парах, представляя её в виде F_mp=f_пр·N, (3.15)

Где f_пр- приведенный коэффициент трения, учитывающий коэффициент трения материалов , форму и размеры элементов кинематической пары и характер приложения силы.