1. Основные понятия и определения ТММ. Механизмом называется система, состоящая из звеньев и кинематических пар, образующих замкнутые или разомкнутые цепи, которая предназначена для передачи и преобразования перемещений входных звеньев и приложенных к ним сил в требуемые перемещения и силы на выходных звеньях. Звено - твердое тело или система жестко связанных тел, входящих в состав механизма. Кинематическая цепь - система звеньев, образующих между собой кинематические пары. Кинематические цепи подразделяют на простые и сложные, открытые и замкнутые, плоские и пространственные. Кинематическая пара - подвижное соединение двух звеньев, допускающее их определенное относительное движение. Стойка - звено, которое при исследовании механизма принимается за неподвижное. Число степеней свободы или подвижность механизма - число независимых обобщенных координат однозначно определяющее положение всех его звеньев на плоскости или в пространстве. Входные звенья - звенья, которым сообщается заданное движение и соответствующие силовые факторы (силы или моменты); Выходные звенья - те, на которых получают требуемое движение и силы. Деталь - часть механизма, выполненная без сборочных операций. Машина - техническое устройство, выполняющее преобразование энергии, материалов и информации с целью облегчения физического и умственного труда человека, повышения его качества и производительности.

2. Основные виды механизмов. Механизмом называется система, состоящая из звеньев и кинематических пар, образующих замкнутые или разомкнутые цепи, которая предназначена для передачи и преобразования перемещений входных звеньев и приложенных к ним сил в требуемые перемещения и силы на выходных звеньях.

 Среди всего многообразия конструкций механизмов различают: стержневые (рычажные), кулачковые, фрикционные, зубчатые механизмы, механизмы с гибкими звеньями (например, ременные передачи) планетарные, манипуляторы и др. виды. Их подразделяют: 1.по виду передаточной функции на механизмы:

с постоянной передаточной функцией;

с переменной передаточной функцией:

2.по виду кинематических пар (КП):

с низшими КП ( все КП механизма низшие );с высшими КП ( хотя бы одна КП высшая );

шарнирные ( все КП механизма вращательные - шарниры ).

3.по способу передачи и преобразования потока энергии:

фрикционные(сцепления);зацеплением;волновые(создание волновой деформации);импульсные.

4.по форме, конструктивному исполнению и движению звеньев:

рычажные, зубчатые, кулачковые, планетарные, манипуляторы.

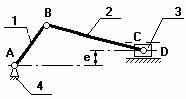
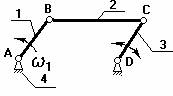кривошипно- шатунный механизм четырехшарнирный механизм.

 

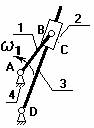
 Кулисный механизм.

Учитывая возможность условного превращения практически любого механизма с высшими парами в рычажный, в дальнейшем наиболее подробно рассматривается именно эти механизмы, а структурные схемы других механизмов изложены в соответствующих разделах.

Среди рычажных механизмов наиболее распространенны так называемые четырехзвенные.

            В этих механизмах встречаются однотипные звенья: кривошип – звено, совершающее полнооборотное вращательное движение вокруг неподвижной оси; коромысло – звено, совершающее неполнооборотное вращательное движение вокруг неподвижной оси; ползун – звено, совершающее поступательное движение относительно стойки; камень – звено, совершающее поступательное движение относительно подвижной направляющей, называемой кулисой; шатун – звено, совершающее плоскопараллельное движение.

3. Кинематические цепи. Кинематические соединения. Движение твердых тел в механизмах рассматривают относительно звена, принимаемого условно за неподвижное и называемого стойкой (станина станка, корпус двигателя, шасси). Все остальные твердые тела, совершающие движение относительно стойки, называют подвижными звеньями. Каждое звено может состоять из одной или нескольких деталей, но в составе звена они не могут иметь относительного движения, т.е. образуют неразъемные или разъемные соединения отдельных деталей. По выполняемым функциям звенья могут быть входными и выходными, ведущими и ведомыми, начальными и промежуточными. Входному звену сообщается движение, преобразуемое механизмом в требуемое движение других звеньев. Ведущее звено– звено, для которого элементарная работа внешних сил, приложенных к нему, является положительной. Выходное звено – звено, совершающее движение, для выполнения которого предназначен механизм. Ведомое звено – звено, для которого элементарная работа приложенных к нему внешних сил отрицательна или равна нулю. кинематической парой называют соединение двух твердых тел механизма, допускающее их заданное относительное движение. В паре при взаимодействии ее элементов происходит относительное движение звеньев. Число степеней свободы в относительном движении звеньев определяет вид пары по подвижности. Систему звеньев, соединенных между собой парами, называют кинематической цепью. Различают плоские и пространственные, замкнутые и незамкнутые, простые и сложные кинематические цепи.

В замкнутой цепи звенья образуют один или несколько контуров. Контур может быть жестким или иметь степени свободы. Количество степеней свободы определяет класс контура. В плоской цепи все подвижные звенья совершают плоское движение, параллельное одной и той же неподвижной плоскости. В простой цепи звено входит в одну или две кинематические пары.

Аналогами кинематических пар являются кинематические соединения, выполненные из нескольких подвижных деталей с поверхностным, линейным или точечным контактом элементов в форме компактной конструкции и обеспечивающей возможность разложения относительного движения на составляющие, эквивалентные парам соответствующего вида.

Схему механизма, содержащую стойку, подвижные звенья, кинематические пары с обозначением их вида и указывающую взаимное расположение элементов механизма, выполненную без масштаба, называютструктурной схемой механизма.

4. Механизмы плоские и пространственные. Число свободы механизма и его определение.

Плоский механизм- мех. , в котором все точки и звенья перемещаются в плоскостях // между собой.

Пространственный мех.- мех., в котором все точки и звенья перемещаются в плоскостях не // между собой.

W число степеней свободы мех-ма. W=1 – для плоских мех-мов Wне= 1 – для пространственных мех-мов Определение числа степеней свободы мех-ма W=3*n-2*P5-P4- формула Чебышева для плоских мех-мов. W-число степеней свободы n-число подвижных звеньев Р5-число пар 5-го класса мех-ма Р4-число пар 4-го класса мех-ма Для плоских мех-мов если Wне= 1 то допущена ошибка, либо присутствуют звенья, создающие лишнюю степень свободы.

5. Структурный синтез механизмов на примере плоского механизма Осн. пр-п образования мех-ов был впервые сформулирован в 1914 г. Л. В. Ассуром. Им был продолжен и развит м-д образования мех-ов путем последовательного наслоения кинематических цепей, обладающих опред. структурными св-ми. Этот м-д легко проследить, рассматривая какой либо конкретный механизм, например :

Этот мех-м имеет 5 подвижных звеньев, образующих семь кинематических пар 5 класса. Сл-но, по ф-ле Чебышева число его степеней свободы равно W=3*n-2*P5=3*5-2*7=1т. е. данный мех-м обладает одной степенью свободы. Выберем в качестве начального звено 2. Тогда мех-м будет состоять из нач. звена 2, обладающего одной степенью свободы, стойки 1 и звеньев, образующих кинематическую цепь, состоящую из звеньев 3, 4, 5 и 6. Процесс образования этого мех-ма можно представить как последовательное присоединение к начальному звену 2 и к стойке 1 кинематической цепи, состоящей из звеньев З и 4. Тогда получим четырехзвенный механизм АВCD, обладающий одной степенью свободы. Далее к звену 4 механизма AВСD и стойке 1 присоединим кинематическую цепь, состоящую из звена 5 и ползуна 6. Тогда получим 6-звенный мех-м, обладающий также одной степенью свободы. Нетрудно теперь установить определенную закономерность процесса образования мех-ма. В самом деле, любой мех-м имеет одно неподвижное звено (стойку). У данного мех-ма стойкой будет звено 1. далее, мех-м должен иметь число начальных звеньев, равное числу его степеней свободы. В нашем случае мех-м обладает одним начальным звеном 2, так как степень свободы мех-ма равна W=1. Т.к. после присоединения звеньев 3, 4, 5 и б число степеней свободы всего мех-ма осталось равным W=1, то, след-но, кинематическая цепь, состоящая из звеньев 3, 4, 5 и 6, присоединенных к нач. звену 2 и стойке 1, обладает нулевой степенью свободы относительно тех звеньев, к которым эта цепь присоединяется. При последовательном присоединении групп необходимо руководствоваться определенными правилами. При образовании мех-ма с одной степенью свободы 1-я группа присоединяется свободными эл-ми звеньев к нач. звену и к стойке. Последующие группы могут присоединиться к любым звеньям полученного мех-ма только так, чтобы звенья группы обладали подвижностью друг относительно друга.

6. Принцип образования механизмов, впервые сформулированный Л.В. Ассуром:

схема любого механизма может быть составлена последовательным присоединением к механизму I класса групп звеньев с нулевой степенью подвижности – групп Ассура.

Группа Ассура - незамкнутая кинематическая цепь с нулевой степенью подвижности. Сколько бы групп Ассура ни присоединяли к механизму I класса, степень подвижности механизма остаётся равной единице.

Для плоского механизма, состоящего только из кинематических пар 5-го класса, степень подвижности групп Ассура определится согласно формуле Чебышева

Поскольку n и p5 могут быть только целыми числами, из равенства следует, что в группах Ассура возможны след. сочетания количества звеньев и примыкающих к ним кинематических пар:

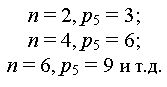
Практически встречаются только первые два сочетания

Разложение механизма на структурные группы необходимо для решения задач кинематического и динамического анализа, обеспечивая статическую определимость составляющих частей схем плоских механизмов.

Структурный анализ механизма следует проводить путём расчленения его на структурные группы в порядке, обратном образованию механизма.

Выделение групп Ассура начинают с наиболее удалённой группы (последней в порядке присоединения к механизму I класса). В результате отсоединения структурных групп остается механизм I класса.