26. Исследование работы электропривода при изменении напряжения

Судовая электростанция является автономной и ограниченной по мощности. Регуляторы напряжения и частоты вращения для обеспечения устойчивой параллельной работы генераторов обладают известным статизмом. При этом допускается определённая свобода в выборе уставки регулируемых параметров. В результате с учётом разной удаленности потребителей от шин ГРЩ, могут сложиться условия работы электроприводов, связанные с длительным отклонением напряжения и частоты, в основном с понижением.

Рассмотрим устойчивость работающего привода при длительном снижении напряжения, но при номинальной частоте.

С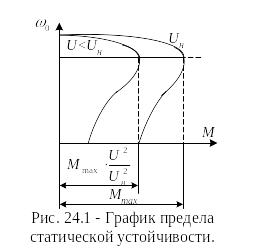 татическая устойчивость привода для любой работающей точки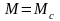 обычно выражается неравенством 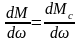>0. Это неравенство будет соблюдаться для АД на участке характеристики в зоне скольжения 0<S<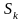 . Учитывая что критическое скольжение не зависит от напряжения, условия устойчивой работы привода при снижении напряжения определяется следующим неравенством

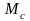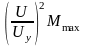< . (24.1)

Откуда минимальное напряжение, обеспечивающее устойчивую работу привода при условии 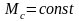будет

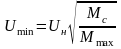. (24.2)

На графике хорошо виден предел статической устойчивости. Если момент сопротивления имеет квадратичную зависимость от скорости 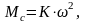что свойственно центробежным нагнетателям, то

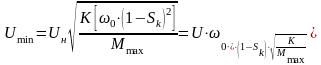(24.3)

С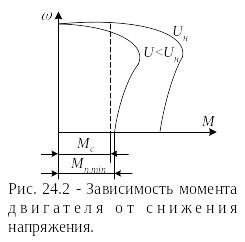 нижение напряжения отражается также на пусковом моменте двигателя. Для трогания двигателя при пуске необходимо, чтобы его пусковой момент имел некоторое превышение над моментом сопротивления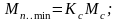 Тогда для устойчивости привода при пуске

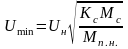, (24.4)

где 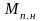- пусковой момент при .

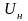Уменьшение момента двигателя, вызванного снижением U, существенно увеличивает время разгона привода. Причем кратность затягивания пускового периода повышается больше чем кратность уменьшения напряжения. Это значительно повышает пусковые потери двигателя.

27. Исследование работы электропривода при изменении частоты

Электромагнитная мощность двигателя

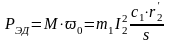; (24.1.1)

отсюда, заменив 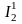через напряжение и эквивалентное сопротивление получим

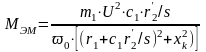(24.1.2)

где 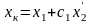- индуктивное сопротивление фазы короткого замыкания.

Исследовав это уравнение на максимум, можно найти значение критического скольжения

.

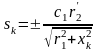Знак «-» соответствует генераторному режиму.

Подставив 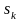в формулу М_эмполучим

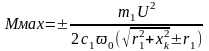. (24.1.3)

Для двигателей большей мощности активное сопротивление статора на порядок меньше Хк т.е. им можно пренебречь. Тогда

;

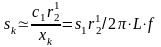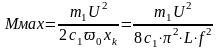. (24.1.4)

Таким образом, длительное уменьшение частоты пропорционально повышает критическое скольжение и пропорционально квадрату частоты увеличивает опрокидывающий момент.

Реализация формулы Клосса с учетом постоянства напряжения позволяет установить значения рабочего скольжения при изменении частоты:

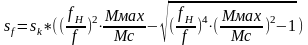, (24.1.5)

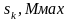-параметры при fн.

Изменение рабочего скольжения и частоты отразится на значении приведенного тока ротора, относительное изменение которого выразится формулой

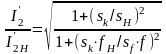, (24.1.6)

т.е. с уменьшением частоты приведенный ток ротора растет. Потери в двигателе увеличиваются.

Момент центробежных нагнетателей при уменьшении частоты вращения уменьшается, что в свою очередь приводит к уменьшению рабочего скольжения .

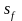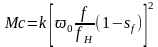. (24.1.7)

В связи с этим, энергетические потери в роторе, как правило, не превосходят номинальные в случаях, когда глубина снижения частоты не превосходит 10-12%. При уменьшении частоты происходит увеличение максимального и пускового момента, что повышает устойчивость работы привода.