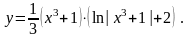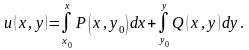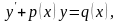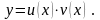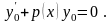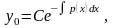4. Рівняння в повних диференціалах

Рівняння виду

, (4.5)

називається рівнянням у повних диференціалах, якщо його ліва частина є повним диференціалом деякої функції 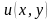, тобто

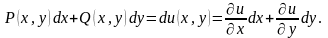
Загальний інтеграл рівняння (4.5) має вигляд

Для того щоб рівняння (4.5) було рівнянням у повних диференціалах, необхідно і достатньо, щоб

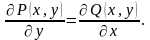
Функцію знаходять за формулою

(4.6)

При цьому в формулі (4.6) нижні границі інтегралів (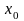 і ) довільні; їх вибір обмежений єдиною умовою – інтеграли в правій частині цієї формули повинні мати сенс (тобто не бути розбіжними невласними інтегралами другого роду). Якщо умова не виконується, то існує така функція 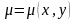, що 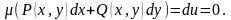Функція 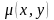називається інтегрувальним множником і задовольняє умові

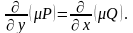
Приклади. Знайти загальний інтеграл рівняння.

1.

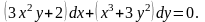
Тут

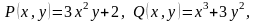
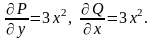
Отже, ліва частина рівняння являється повним диференціалом деякої функції , тобто

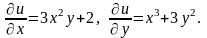
Проінтегруєм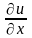о по :

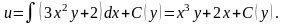
Знайдемо функцію 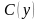, продиференціювавши останній вираз по :

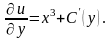
Одержуємо рівняння

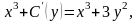
звідки знаходимо

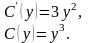
Таким чином, загальний інтеграл рівняння має вигляд:

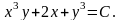
2.

Тут

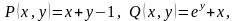
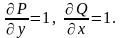
Таким чином, умова повного диференціала виконана, тобто дане рівняння є рівнянням у повних диференціалах.

Знайдемо загальний інтеграл за формулою

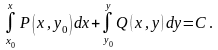
Прийнявши 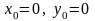, одержимо

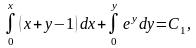
або

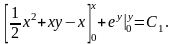
Підставляючи границі маємо

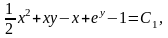
або

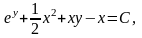де

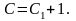
5. Лінійні диференціальні рівняння першого порядку

Лінійним диференціальним рівнянням першого порядку називається рівняння виду

(5.7)

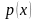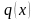де і – задані і неперервні на деякому проміжку функції.

а) Метод Бернуллі розв’язку лінійних рівнянь

Шукаємо розв’язок рівняння (5.7) у вигляді добутку двох функцій 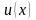і 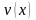, тобто використовуємо підстановку виду

(5.8)

Тоді вираз для похідної матиме вигляд

.

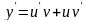Після підстановки виразів для і в рівняння (5.7) і, групуючи доданки в ньому, наприклад, наступним чином

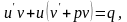
одержимо два рівняння з відокремлюваними змінними:

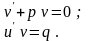
Приклади. Розв’язати рівняння.

1. .

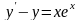Це лінійне рівняння

Використаємо підстановку

; .

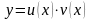Підставимо і в рівняння і групуємо доданки наступним чином:

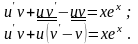
Вираз у дужках вважаємо рівним нулю:

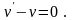
Відокремлюючи змінні, маємо:

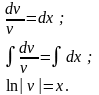
Звідси маємо: 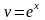. З урахуванням знайденого виразу для маємо рівняння для визначення функції :

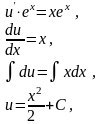
де – константа інтегрування.

Загальний розв’язок рівняння матиме вигляд

2.

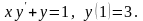
Переписавши дане рівняння у вигляді

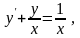
легко переконатись, що воно є лінійним. Як і раніше використаємо підстановку

; .

Тоді

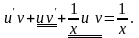
Групуючи підкреслені доданки маємо:

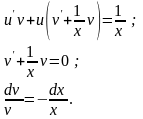
Інтегруючи послідовно рівність, знаходимо:

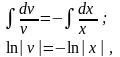
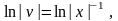звідси

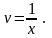
Далі знаходимо із співвідношення:

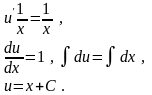
Загальний розв’язок має вигляд:

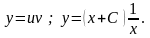
Знайдемо частинний розв’язок, який задовольняє початковій умові

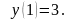
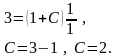
Отже, отримали частинний розв’язок

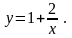
б) Метод варіації довільної сталої

Якщо в правій частині рівняння (5.7) функція 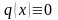, то лінійне рівняння називається лінійним однорідним. Лінійне однорідне рівняння завжди є рівнянням з відокремлюваними змінними.

Метод варіації довільної сталої полягає в наступному: шукаємо розв’язок однорідного лінійного рівняння, яке відповідає даному, тобто

(5.9)

Легко переконатись, що загальний розв’язок однорідного лінійного рівняння (5.9) буде мати вигляд

(5.10)

де – довільна стала.

Вважаємо в загальному розв’язок однорідного рівняння (5.10) функцією від , тобто 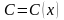. Підставляючи вирази для і (знайдені з урахуванням того, що ) в початкове рівняння (5.7), одержимо після нескладних перетворень рівняння з відокремлюваними змінними відносно невідомої функції .

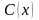Приклади. Розв’язати рівняння.

1.

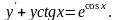
Запишемо відповідне однорідне рівняння

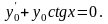
Розв’язуємо його відокремлюючи змінні:

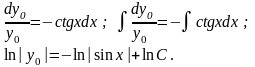
Користуючись властивостями логарифмів, знаходимо:

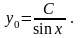
Вважаємо , тоді

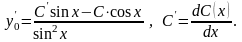
Підставляємо вирази для і в початкове рівняння:

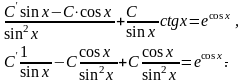
Звідки

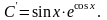
Оскільки 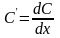, то

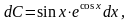
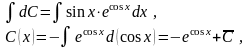
де 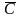– нова довільна стала інтегрування.

Загальний розв’язок має вигляд

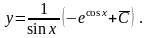
2.

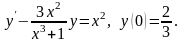
Відповідне однорідне рівняння має вигляд:

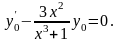
Відокремлюючи змінні, знаходимо:

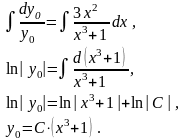
Вважаємо , тоді

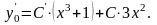
Підставляємо в початкове рівняння, знаходимо:

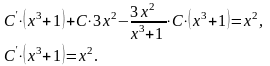
Тоді

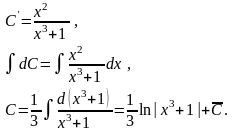
Тоді загальний розв’язок має вигляд

.

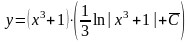Визначимо значення сталої при початковій умові:

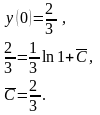
Частинний розв’язок має вигляд: