
- •Диференціальні рівняння першого порядку
- •1. Загальні поняття та означення
- •2. Диференціальні рівняння першого порядку з відокремлюваними змінними Рівняння виду
- •Рівняння виду
- •Загальний інтеграл диференціального рівняння (2.2) має вигляд
- •3. Однорідні диференціальні рівняння
- •4. Рівняння в повних диференціалах
- •5. Лінійні диференціальні рівняння першого порядку
- •6. Рівняння бернуллі
- •7. Задачі на складання диференціальних рівнянь
- •Варіанти індивідуальних завдань Зміст роботи
- •Список літератури
- •1. Загальні поняття та означення.......................................................…....3
- •Список літератури......................................................................…....31
Диференціальні рівняння – один з найважливіших розділів курсу вищої математики, знання їх необхідне при вивченні електротехніки, теоретичної механіки, опору матеріалів, при моделюванні різноманітних фізичних і технічних проблем.
Диференціальні рівняння першого порядку
1. Загальні поняття та означення
Диференціальним рівнянням першого порядку називається рівняння виду
|
(1.1) |
яке
пов’язує незалежну змінну
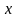 ,
невідому функцію
,
невідому функцію
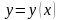 та її похідну, або, якщо його розв’язати
відносно похідної
та її похідну, або, якщо його розв’язати
відносно похідної
|
|
Розв’язком
диференціального рівняння
(1.1) на деякому інтервалі
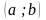 називається диференційована на цьому
інтервалі функція
називається диференційована на цьому
інтервалі функція
 ,
яка при підстановці в рівняння (1.1)
перетворює його в тотожність по
на
.
,
яка при підстановці в рівняння (1.1)
перетворює його в тотожність по
на
.
Приклади.
1.
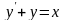 –
диференціальне рівняння першого порядку.
Його розв’язком є функція
–
диференціальне рівняння першого порядку.
Його розв’язком є функція
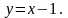
Дійсно,
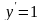 ,
тоді
,
тоді
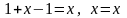 –
одержали тотожність.
–
одержали тотожність.
2.
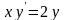 ,
розв’язком диференціального рівняння
є функція
,
розв’язком диференціального рівняння
є функція
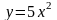 .
Дійсно,
.
Дійсно,
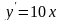 ,
тоді
,
тоді
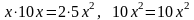 –
одержали тотожність.
–
одержали тотожність.
Функція
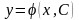 ,
яка залежить від аргументу і довільної
сталої
,
яка залежить від аргументу і довільної
сталої
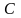 ,
називається загальним
розв’язком
рівняння (1.1) в області
,
називається загальним
розв’язком
рівняння (1.1) в області
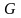 ,
якщо вона задовольняє дві умови:
,
якщо вона задовольняє дві умови:
1)
функція
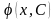 є розв’язком рівняння при будь-якому
значенні сталої
з деякої множини;
є розв’язком рівняння при будь-якому
значенні сталої
з деякої множини;
2)
для довільної точки
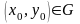 можна знайти таке значення
можна знайти таке значення
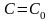 ,
що функція
,
що функція
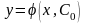 задовольняє початкову умову:
задовольняє початкову умову:
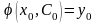 .
.
Частинним розв’язком рівняння (1.1) називається функція , яка утворюється із загального розв’язку при певному значенні сталої .
Задача,
в якій необхідно знайти частинний
розв’язок
рівняння (1.1), який задовольняє початковій
умові
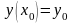 ,
називається задачею
Коші.
,
називається задачею
Коші.
Якщо
загальний розв’язок диференціального
рівняння знайдено в неявному вигляді,
тобто у вигляді рівняння
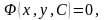 то такий розв’язок називають загальним
інтегралом диференціального рівняння
(1.1). Рівність
то такий розв’язок називають загальним
інтегралом диференціального рівняння
(1.1). Рівність
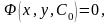 називають частинним
інтегралом рівняння.
називають частинним
інтегралом рівняння.
Приклади.
1.
Перевірити, що функція
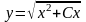 являється загальним розв’язком
диференціального рівняння
являється загальним розв’язком
диференціального рівняння
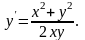
Знаходимо
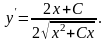
Підставляємо в рівняння:
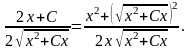
Або після перетворень одержимо тотожність
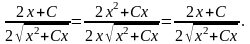
2.
Знаючи, що функція
 –
загальний розв’язок рівняння
–
загальний розв’язок рівняння
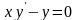 ,
знайти частинний розв’язок, який
задовольняє початковим умовам
,
знайти частинний розв’язок, який
задовольняє початковим умовам
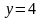 при
при
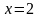 .
.
Легко переконатись у тому, що функція дійсно являється загальним розв’язком заданого рівняння, так як
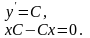
Задовольняючи початковим умовам, знаходимо:
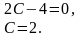
Отже, частинний розв’язок має вигляд:

З
геометричної точки зору загальний
інтеграл визначає на координатній
площині сім’ю кривих, залежну від
довільної сталої. Частинному розв’язку
відповідає одна крива цієї сім’ї, що
проходить через задану точку. В кожній
точці така крива, яка називається
інтегральною кривою, буде мати дотичну
з кутовим коефіцієнтом
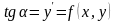 .
Сукупність трійок
.
Сукупність трійок
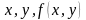 утворює так зване поле
напрямків.
Геометричне місце точок з однаковим
напрямом поля
утворює так зване поле
напрямків.
Геометричне місце точок з однаковим
напрямом поля
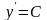 називають ізоклінами.
називають ізоклінами.
Для задачі Коші і є теорема про існування та єдиність розв’язку.
Якщо
функція
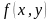 неперервна в області D разом зі своєю
частинною похідною
неперервна в області D разом зі своєю
частинною похідною
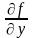 ,
тоді для будь-якої точки (х0,у0),
яка належить області D, задача Коші має
і причому єдиний розв’язок, визначений
в деякому околі точки х0.
,
тоді для будь-якої точки (х0,у0),
яка належить області D, задача Коші має
і причому єдиний розв’язок, визначений
в деякому околі точки х0.
Приклади. 1. Знайти область існування та єдиності розв’язків диференціального рівняння
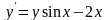 .
.
Оскільки
права частина заданого рівняння та
частинна похідна
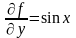 є
неперервними функціями в усій дійсній
площині, то рівняння має єдиний розв’язок
для будь-якої точки (х0,у0).
є
неперервними функціями в усій дійсній
площині, то рівняння має єдиний розв’язок
для будь-якої точки (х0,у0).
2. Знайти область існування та єдиності розв’язків рівняння
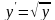 .
.
Права
частина заданого рівняння визначена і
неперервна при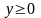 .
Оскільки частинна похідна
.
Оскільки частинна похідна
 не
є неперервною при у=0, то в точках прямої
у=0 умови теореми не виконуються, тобто
рівняння має більше одного розв’язку.
не
є неперервною при у=0, то в точках прямої
у=0 умови теореми не виконуються, тобто
рівняння має більше одного розв’язку.

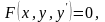
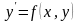 .
.