Примечание: «Средние» хитрости.

Среднее арифметическое Х = å хi

n

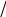
Среднее геометрическое Х = ⁿ х1_*х2_*х3….хn

n

Среднее гармоническое Х = å ¹ хi

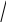
Среднее квадратичное Х = å х²i

n

Среднее кубическоеое Х = 3 å х³i

n

Правило мажоритарности средних: Хгарм £ Хгеом£ Хариф£ Хквадр£ Хкуб

Пример: найдем среднее между “парой” и “отлично”.

1. среднее гармоническое = 2,86 » 3

2. среднее геометрическое = 3,16 » 3

3. среднее арифметическое = 3,5

4. среднее квадратичное = 3,81 » 4

5. среднее кубическое = 4,05 » 4

Задачи:

1. Покупка автомобиля

Критерий	А1	А2	А3
Цена (тыс.$)	15	17	17,5
Тип кузова	пикап	седан	универсал
Приемистость (сек)	6	8	7
Мощность (куб.см)	1,8	2	2,2

2. Выбор учебного курса

Критерий	А1	А2	А3
Стоимость (руб.)	5000	3500	4000
Срок обучения (мес.)	4	2,5	3
Получаемый разряд	1	3	2
Время на дорогу (час)	2	1	1,5

3. Наем работника

Критерий	А1	А2	А3
Возраст	25	35	45
Стаж	2	8	12
Квалификация (разряд)	4	2	1
Требуемая зарплата	4500	9000	8000

4. Поездка

Критерий	А1	А2	А3
Время (час)	2	24	30
Стоимость (руб.)	1200	800	600
Уровень комфорта	1	2	4
Доп. дор. затраты (час)	3	1,5	0

Тема: Метод дерева решений (модифицированный)

Метод дерева решений используется при отборе альтернатив, когда мы сталкиваемся с достаточно сложными решениями, которые можно уточнять и конкретизировать в разных вариантах. Дерево решений позволяет наглядно представить их многообразие и взаимосвязи. Последовательно «спускаясь» по дереву и проверяя варианты с точки зрения приемлемости, мы выходим на удовлетворяющие нас конкретные решения, среди которых и делаем окончательный выбор.

Проблема

Да

Нет

Да

Нет

Нет

Да

Нет

Да

Нет

Нет

выбор

Несмотря на простоту и наглядность, использование данного метода не позволяет ответить на ряд вопросов, которые могут сыграть существенную роль при ПУР:

1. данный метод не всегда приводит к однозначному результату

2. мы вынуждены использовать только один критерий («да»-«нет») для достаточно разнокачественных альтернатив

3. мы не в состоянии получить количественные оценки

Избавиться от вышеперечисленных недостатков метода дерева решений мы можем, скомбинировав его с методом оценочных таблиц.

Рассмотрим конкретный пример.

0,49

0,126 Г1 0,60

за ужином

Д1

0,51

с гостями с гостями 0,43

0,132 Г2

за беседой В1

0,52

остаться

0,089 Г3 0,40 дома

в одиночестве

Д2

0,48

без гостей

0,083 Г4

лечь спать

0,53

Встреча

0,124 Г5 0,41 Нового Б

за ужином года

Д3

0,47

к родным и

0,110 Г6 знакомым

за беседой

0,40

0,091 Г7 0,40 0,57

в своей стране

Д4 В2

0,60

через бюро

0,137 Г8 путешествий уехать

за рубежом

1,00 0,19

0,108 Г9 Д5

новогодний бал в местах общественных увеселений

Выделим в данном дереве 8 семейств («мать»-«дочки»)

1. Б, В1, В2

2. В1, Г1, Г2

3. В2, Г3, Г4, Г5

4. Г1, Д1, Д2

5. Г2, Д3, Д4

6. Г3, Д5, Д6

7. Г4, Д7,Д8

8. Г5, Д9

В каждом семействе альтернативы сравниваются между собой.

Последнее семейство у нас получилось «усеченным», безальтернативная «дочка» необходима только для того, чтобы довести ветвь до нижнего уровня.

Поскольку качественно элементы значительно отличаются, необходимо несколько критериев, чтобы можно было выделить характерные для каждого семейства.

Для примера выделим следующие критерии оценки:

1. денежные расходы

2. затраты времени на подготовку

3. степень новизны

4. ожидаемые впечатления

5. возможные негативные последствия

6. пожелания гостей

7. собственные склонности

8. желательные встречи

Рассмотрим в качестве примера одно из семеств – семейство 3.

Выделим для него наиболее существенные на наш взгляд критерии оценки и проранжируем их с точки зрения значимости при помощи весовых коэффициентов К (сумма которых должна равняться 1)

степень новизны – 0,3

ожидаемые впечатления – 0,2

денежные расходы – 0,2

желательные встречи – 0,3

å = 1

Затем оцениваем альтернативы по каждому критерию с точки зрения предпочтительности опять же при помощи весовых коэффициентов ( å=1 ) и рассчитываем обобщенную «эффективность» каждой из трех альтернатив данного семейства.

Критерии	К	Д1	Д2	Д3	å
Степень новизны	0,3	0,1	0,7	0,2	1
Ожидаемые впечатления	0,2	0,1	0,7	0,2	1
Денежные расходы	0,2	0,6	0,1	0,3	1
Желательные встречи	0,3	0,8	0,1	0,1	1
å	1	0,41	0,40	0,19

Аналогичные таблицы рассчитываем для каждого семейства, получая для каждого элемента соответствующую оценку эффективности. При этом необходимо соблюдать следующие условия:

1. все ветви надо довести до нижнего уровня (см. Г9)

2. если на том или ином уровне семейства имеют различное количество альтернатив-«дочек», то во избежании искажения результатов, необходимо вводить коэффициенты ветвления.

На следующем этапе остается перемножить оценки элементов, относящиеся к каждой ветви. В нашем случае:

Ветвь 1 (Б . . . Г1) : 0,43*0,60*0,49=0,126 третье место

Ветвь 2 (Б . . . Г2) : 0,43*0,60*0,51=0,132 второе место

Ветвь 3 (Б . . . Г3) : 0,43*0,40*0,52=0,089

Ветвь 4 (Б . . . Г4) : 0,43*0,40*0,48=0,083

Ветвь 5 (Б . . . Г5) : 0,57*0,41*0,53=0,124

Ветвь 6 (Б . . . Г6) : 0,57*0,41*0,47=0,110

Ветвь 7 (Б . . . Г7) : 0,57*0,40*0,40=0,091

Ветвь 8 (Б . . . Г8) : 0,57*0,40*0,60=0,137 первое место

Ветвь 9 (Б . . . Г9) : 0,57*0,19*1,00=0,108

Сумма=1,000 (совершенно понятно!)

Общий алгоритм применения модофицированного метода

дерева решений:

1. Формулирование цели

2. Анализ ситуации с учетом цели

3. Формулирование проблемы = цель – ситуация

4. Декомпозиция проблемы

5. Разработка критериев оценки

6. Разработка вариантов основных решений, оценка их эффективности

7. Разработка детализированных решений по каждому из оставшихся основных решений. Оценка эффективности.

8. Разработка детализированных вариантов по каждому из оставшихся детализированных решений. Оценка эффективности.

9. Оценка каждой ветви с точки зрения возможности и эффективности

10. Выбор наиболее приемлемой ветви и реализация

Тема: Метод парных сравнений (парная сортировка)

и метод поэтапного сравнения (метод уступок).

Пример: А1

А1

А2

А3

Альтернативы А3

А4

А4

А5

А5

!Однако, результат может зависеть от порядка сравнения.

Пример: городской бюджет