Анализ устойчивости сау с применением частотного критерия Найквиста

Критерий Найквиста для анализа устойчивости замкнутой САУ опирается на полученное ранее утверждение о том, что рассматриваемая САУ в разомкнутом виде устойчива.

В этом случае по критерию Найквиста для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф АФХ разомкнутой САУ не охватывал точку с координатами (-1; 0)

Выразим АФХ разомкнутой САУ:

Построим годограф АФХ в двух масштабах:

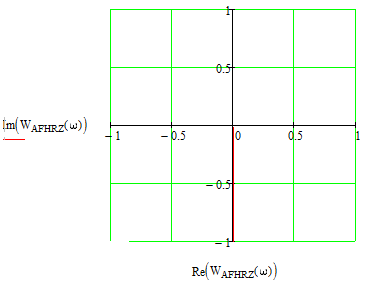
На увеличенном масштабе в области пересечения координатных осей отчётливо видно, что годограф разомкнутой САУ не охватывает точку с координатами (-1; 0), что по критерию Найквиста соответствует устойчивой замкнутой САУ.

Полученный результат подтверждает аналогичный результат, полученный ранее с помощью алгебраического критерия устойчивости.

Анализ путей повышения устойчивости сау

Устойчивость замкнутой САУ в частном рассматриваемом случае можно повысить, варьируя временные и передаточные коэффициенты звена последовательной коррекции.

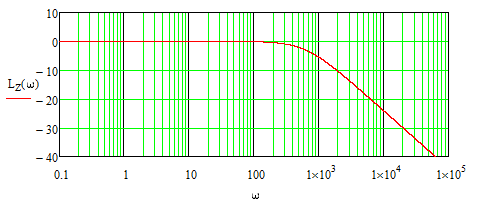
Для более удобной оценки запасов устойчивости по амплитуде и фазе построим ЛАЧХ и ЛФЧХ нескорректированной системы:

Как можно легко увидеть из них, запас устойчивости САУ по амплитуде бесконечен, а по фазе положителен (~90°) , САУ устойчива.

Анализ точности сау в вынужденном режиме Анализ путей повышения точности сау.

В анализируемой САУ присутствует интегрирующее звено в виде редуктора, поэтому значение статической ошибки будет равно нулю независимо от коэффициентов усиления звеньев САУ.

Составим передаточную функцию по ошибке:

_{Разложим в ряд:}

Соберём коэффициенты:

_{Е0 – ошибка по положению (статическая)}

_Е1 – ошибка по скорости

_{Е2 – ошибка по ускорению}

_{Альтернативное нахождение статической ошибки:}

_{Альтернативное нахождение ошибки по скорости:}

_{E0=E00=0, что подтверждает сделанное выше предположение о нулевой статической ошибке ввиду наличия редуктора.}

_{Допустимая по условию постановки задачи статическая ошибка Е0Д=5%=0.05}

_{Е0 < Е0Д ,} что удовлетворяет требованиям к статической ошибке.

Основных способов уменьшения статической ошибки два:

- увеличение коэффициента усиления звеньев САУ

- введение интегрирующего звена, «выбирающего» ошибку с течением времени.

В САУ большой точности наибольшее распространение получил второй способ, как сравнительно более простой в реализации и обеспечивающий лучшие эксплуатационные характеристики. В рассматриваемой САУ применён именно этот способ.

Анализ качества переходного процесса

Частотный метод анализа

_{Переходные процессы можно оценить по одной лишь АЧХ замкнутой САУ.}

_{Выразим и построим её:}

_{Частота среза:}

_{Частотный показатель колебательности переходного процесса:}

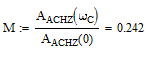
_{Значение частотного показателя колебательности меньше единицы, что соответствует отсутствию колебаний в переходном процессе, переходный процесс апериодичен.}

_{Время переходного процесса: с}

Корневой метод анализа

Характеристическое уравнение замкнутой системы:

Матрица полиноминальных коэффициентов и корни полинома:

_{Время переходного процесса определяется близостью корней ко мнимой оси:}

_с

_{По корням также можно оценить степень колебательности:}

_{, что также соответствует переходному процессу без колебательности.}

Заключение

_{В процессе выполнения курсовой работы были достигнуты все поставленные перед исследователем задачи по анализу и преобразованию линейных систем автоматического управления.}

_{Были составлены передаточные функции разомкнутой и замкнутой (с обратной связью) системы автоматического управления углом перемещения механизма, произведены преобразования звеньев САУ для более удобного исследования.}

_{Произведённый анализ устойчивости по алгебраическим и частотным критериям показал не только полную устойчивость САУ в разомкнутом виде по фазе и амплитуде, но и достаточную устойчивость в замкнутом, что позволило от выработки рекомендаций и внесения корректировки в параметры корректирующих звеньев.}

_{Вслед за анализом устойчивости САУ был проведён анализ точности САУ в вынужденном режиме, результат которого также не потребовал корректировки звеньев САУ. Также по этим результатам были даны рекомендации по повышению точности САУ в общем случае.}

_{На основе анализов устойчивости и точности были произведены частотные и корневые исследования качества переходного процесса, из которых был сделан вывод об апериодическом переходном процессе со временем ~1.2*10}^-3 _c.