IV. Сравнение обыкновенных дробей.

Далее ,при изучении сравнения обыкновенных дробей, полезно рассмотреть решение следующей задачи, в котором прослеживаются все возможные случаи:

Известно, что одна из дробей 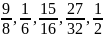находится на числовой прямой между дробями . Найдите эту дробь.

Сначала узнаем, как на числовой прямой расположены дроби . Обратите внимание —у них одинаковые числители. Это значит, что берётся одинаковое количество долей. Однако доли берутся разные: в первой дроби мельче, чем во второй (двенадцатые доли единицы мельче, чем восьмые доли). Следовательно, .

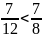А можно было рассуждать так: в первой дроби 7 делится на 12, а во второй то же самое число 7 делится на 8. Значит, первое частное меньше второго. Итак, на числовой прямой дробь 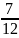будет расположена левее, чем :

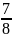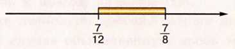
Теперь нужно выбрать среди дробей ту, которая больше , но меньше . Начнём с дроби Её удобно сравнивать с : у этих дробей одинаковые знаменатели, то есть единица делится на одинаковые доли. Значит, больше будет та дробь, в которой этих долей берётся больше: . (а можно было прийти к такому же выводу, заметив, что > 1, а < 1),

то есть нам не подходит.

Для дроби нетрудно найти место по отношению к дроби : :

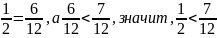Дробь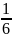 ещё меньше, чем значит, эта дробь нам тоже не подходит:

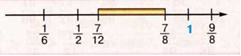
Рассмотрим теперь дробь 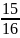. Она похожа на тем, что и у той, и у другой числитель на единицу меньше знаменателя. Эти дроби близки к 1, но первой до 1 не хватает , а второй не хватает . Получается, что первая дробь ближе к 1, следовательно:

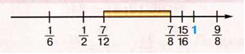
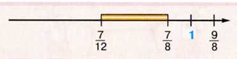
Осталась только одна дробь: 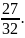Получается, что именно эта дробь должна на числовой прямой оказаться между и . Давайте все-таки проверим, сравнив дроби , и Сравнивать было бы легко, если бы эти дроби имели одинаковые знаменатели. Но ведь мы можем привести все эти дроби к новому знаменателю! Сделаем это.

Новый знаменатель должен делиться на знаменатель каждой из этих дробей, то есть должен быть общим кратным для чисел 12; 8 и 32. Найдём наименьшее общее кратное этих чисел:

НОК(12; 8; 32) = 96.

Приведём все три дроби к новому знаменателю 96:

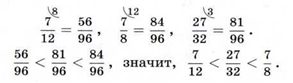
Из решения данной задачи можно сделать вывод:

1. Из двух обыкновенных дробей с одинаковыми знаменателями больше та, у которой больше числитель.

2. Из двух обыкновенных дробей с одинаковыми числителями больше та, у которой меньше знаменатель.

3. Любая правильная обыкновенная дробь меньше любой неправильной.

4. Чтобы сравнить обыкновенные дроби, можно привести их к общему знаменателю (наименьшему общему знаменателю). При этом в качестве нового знаменателя обычно выбирают наименьшее общее кратное знаменателей данных дробей.

V. Рациональные числа.

Далее полезно провести следующий разговор:

Обыкновенные дроби — это положительные числа, однако мы можем рассмотреть и числа, противоположные им, например: и так далее:

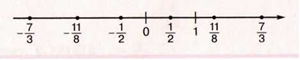
Целые числа (положительные, отрицательные и 0), обыкновенные дроби и числа, противоположные обыкновенным дробям, объединяются одним названием — рациональные числа.

Определение:

Число, которое можно представить в виде ,где а — целое число, b — натуральное, называется рациональным числом.

Убедимся, что под это определение действительно подходят все известные нам числа. Например:

натуральное число: 5 = ;

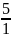число 0: 0 = ;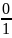

число, противоположное натуральному:

число, противоположное обыкновенной дроби:

смешанное число:

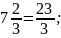
конечная десятичная дробь: 1,23 = .

Труднее убедиться в том, что бесконечную периодическую десятичную дробь тоже можно представить в виде ,где а — целое число, b — натуральное, однако это действительно так. Проверьте, например, что:

0,33333. .. =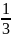 ; 0,181818... = 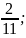2,45555... = .

Вы можете научиться переводить бесконечные периодические десятичные дроби в обыкновенные. Рассмотрим дробь 0,55555...

Обозначим 0,55555... = х.

10х = 5,55555... = 5 + 0,55555... = 5 + х

(бесконечные десятичные дроби умножаются на 10; 100; 1000 и так далее по такому же правилу, как и конечные десятичные дроби). Решим уравнение:

10x = 5 + х;

9х = 5;

х = 5 : 9;

x=

Значит, 0,55555...= .