Методика изучения темы «Рациональные числа»

I. Мотивация.

На этапе мотивации можно предложить учащимся следующий сюжетный фрагмент из сказки:

«Встал Иван-царевич поутру да отправился прямёхонько в сладкую лавку со всякими товарами заморскими. Достал кошель с золотыми монетами, стал гостинец выбирать. Смотрит — пирогов сладких разложено видимо-невидимо.

Покупателей тоже много, да речи все ведут диковинные. Первый, по виду — писарь, просит одну четверть пирога. Ему подают:

Другой мужик просит восемь четвёртых пирога. Ему выкладывают:

Третий требует шесть четвёртых пирога и получает:

Эх, попробую и я! — решился Иван-царевич. — Пожалуйте мне целый пирог!

А лавочник-то не понимает! Написал тогда Иван-царевич в грамотке цифру 1. Один пирог, значит. А лавочник опять не понимает. Осерчал Иван-царевич, схватил пирог сам. Вот, мол, что мне требуется. Понял лавочник, разулыбался.

Четыре четвёртых пирога, — говорит и пишет: .

Уложил Иван-царевич пирог в коробку изукрашенную, бечёвкой перевязал. Взял тот гостинец, вышел на белый свет и думает:

— Что за странность такая? Покупатели и лавочник всё два числа называют да их одно над другим пишут!

Очень любил Иван-царевич всякие забавы с числами, вот и решил он с места не сойти, а в этой странности разобраться».

II. Повторение понятия обыкновенной дроби.

Далее необходимо повторить с учащимися понятие обыкновенной дроби. Можно провести следующий разговор:

Д авайте вспомним, что мы знаем об обыкновенных дробях. Целое (единицу) разделим на 4 равные части (доли), взяли 3 такие доли. Запишем это в виде дроби:

3	числитель
4	знаменатель

Данная дробь читается – «три четвёртых». Обыкновенная дробь равна частному от деления числителя на знаменатель:

Обыкновенную дробь, у которой числитель меньше знаменателя, называют правильной. Если числитель равен или больше знаменателя, дробь называют неправильной.

Например:

Неправильную дробь можно представить в виде смешанного числа или она может оказаться равной натуральному числу:

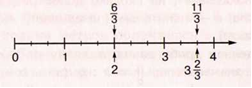
Представление неправильной дроби в виде смешанного числа называют выделением целой части.

Выделить целую часть можно, выполнив деление числителя на знаменатель:

И обратно, смешанное число можно представить в виде неправильной обыкновенной дроби:

Любую обыкновенную дробь можно представить в виде десятичной, выполнив деление числителя на знаменатель:

При этом могут получаться как конечные десятичные дроби, так и бесконечные периодические десятичные дроби:

III. Сокращение обыкновенных дробей.

Изучение сокращения дробей следует начать с рассмотрения рисунка

На этом рисунке закрашено круга. Изменим рисунок – разделим каждую долю пополам:

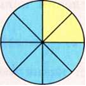
Величина закрашенной части круга не изменилась, но теперь видно, что её можно обозначить и другой дробью: .

При этом обратите внимание — общее количество долей увеличилось в два раза, но и количество выбранных долей также увеличилось в два раза:

Можно было бы на первом рисунке разделить каждую долю не на две, а на три равные части, или на четыре, или на пять, ... И каждый раз одна и та же величина закрашенной части обозначалась бы новой дробью:

Этот пример иллюстрирует основное свойство обыкновенной дроби: «Если числитель и знаменатель обыкновенной дроби умножить на одно и то же натуральное число, величина дроби не изменится».

Заполним пропуск в записи:

Чтобы из знаменателя 3 получить знаменатель 12, нужно умножить его на 4. Значит, чтобы величина дроби не изменилась, нужно и числитель также умножить на 4:

Говорят, что дробь привели к новому знаменателю, а число 4 при этом называют дополнительным множителем.

Рассмотрим полученное равенство с другой точки зрения:

Числитель и знаменатель дроби разделили на одно и то же число (4), при этом величина дроби не изменилась. В этом случае говорят, что дробь сократили на 4. Нам удалось сократить дробь ,потому что её числитель и знаменатель делились на одно и то же натуральное число, то есть имели общий делитель (не равный 1). Однако так бывает не всегда.

Дробь сократить нельзя, так как её числитель и знаменатель не имеют общего натурального делителя, кроме 1 (то есть являются взаимно простыми числами). Такие обыкновенные дроби называются несократимыми.