Розділ 4

Система лінійних диференціальних рівнянь зі сталими коефіцієнтами

Система називається нормальною, коли всі її рівняння розв’язані відносно похідних.

Нормальна система n лінійних диференціальних рівнянь зі сталими коефіцієнтами має вигляд:

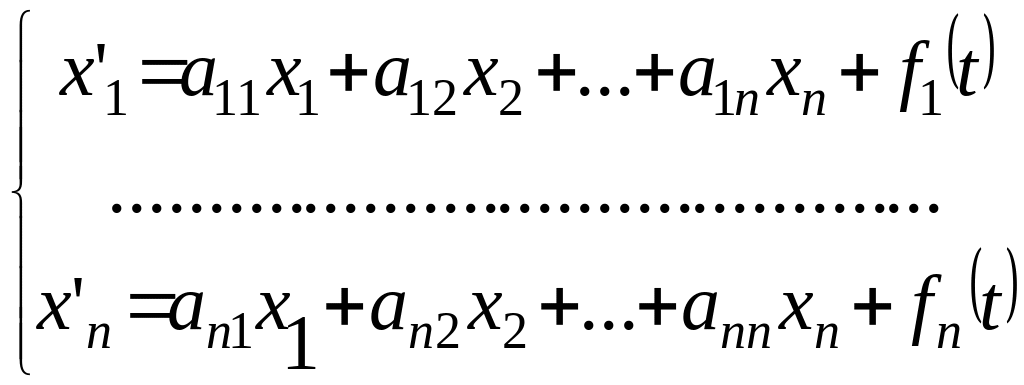, (4.1)

де шукані функції незалежної змінної .

4.1 Однорідні системи

Відповідна (4.1)однорідна система :

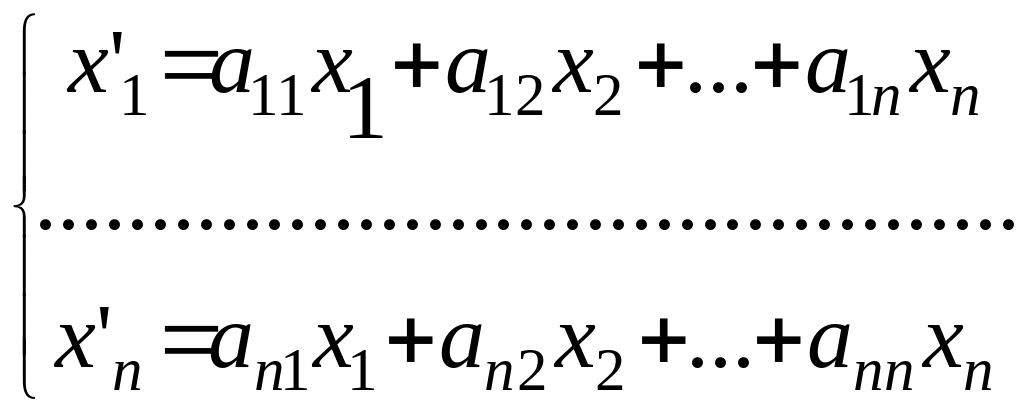, (4.2)

розв’язок якої шукають у вигляді

, (4.3)

де , = .

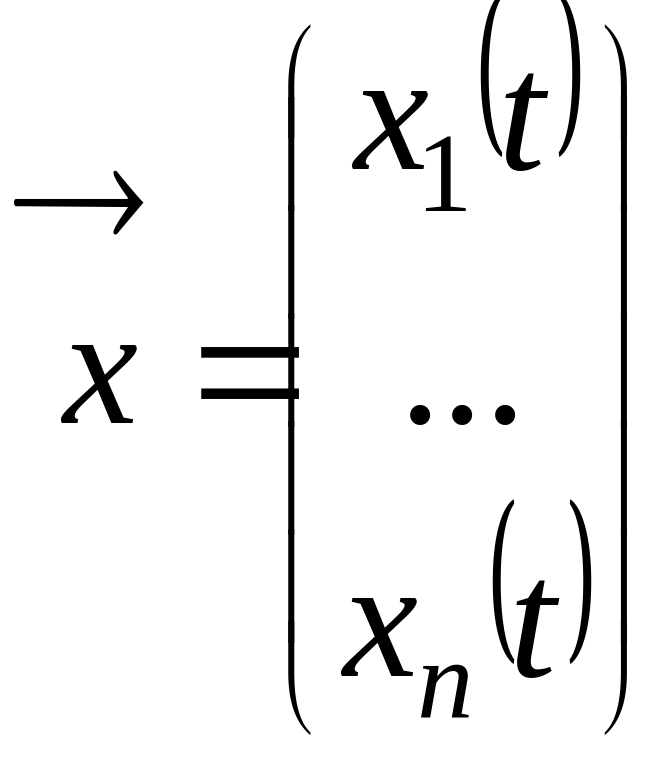Підставивши (4.3) в (4.2) , отримаємо систему лінійних алгебраїчних рівнянь для невідомих

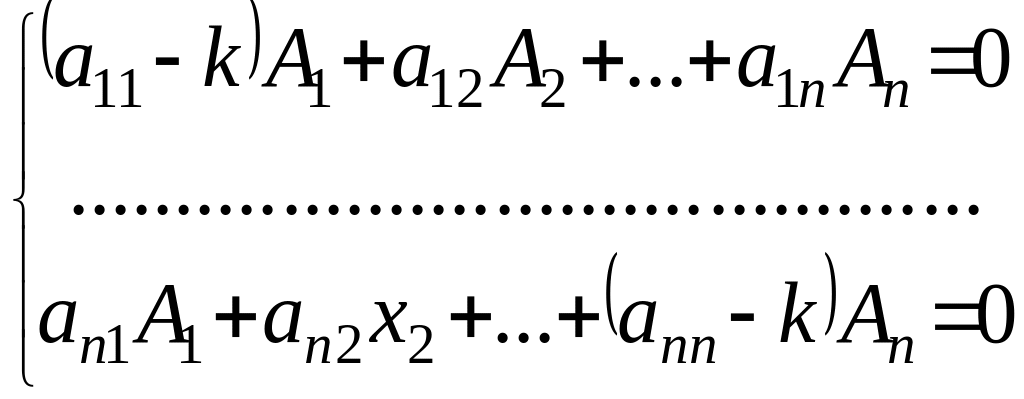, (4.4)

яка має ненульовий розв’язок лише при

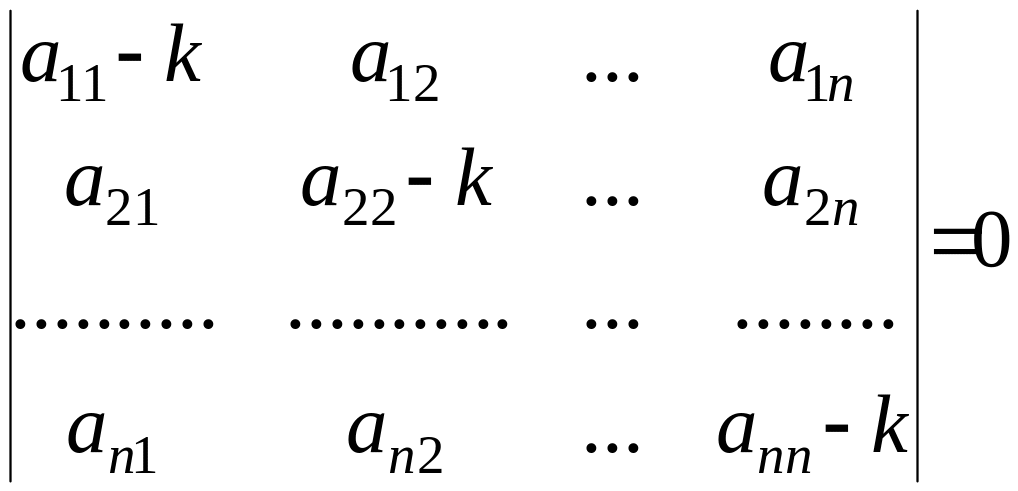= (4.5)

Рівняння (4.5) є характеристичним рівнянням системи (4.2).

Таким чином треба знайти власні значення та власні вектори матриці

.

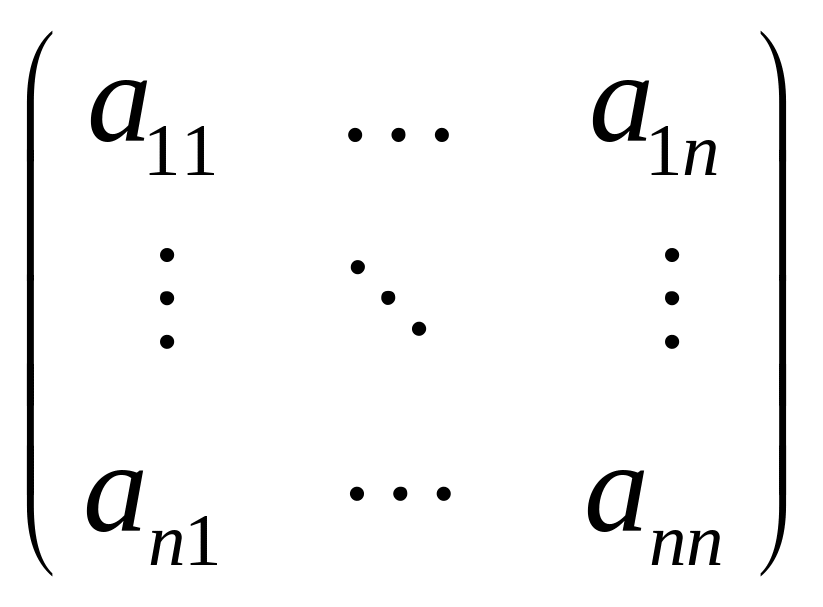Якщо всі n розв’язків рівняння (4,5) різні , то кожному власному значенню відповідає свій власний вектор = .

а загальний розв’язок системи (4.2) буде такий :

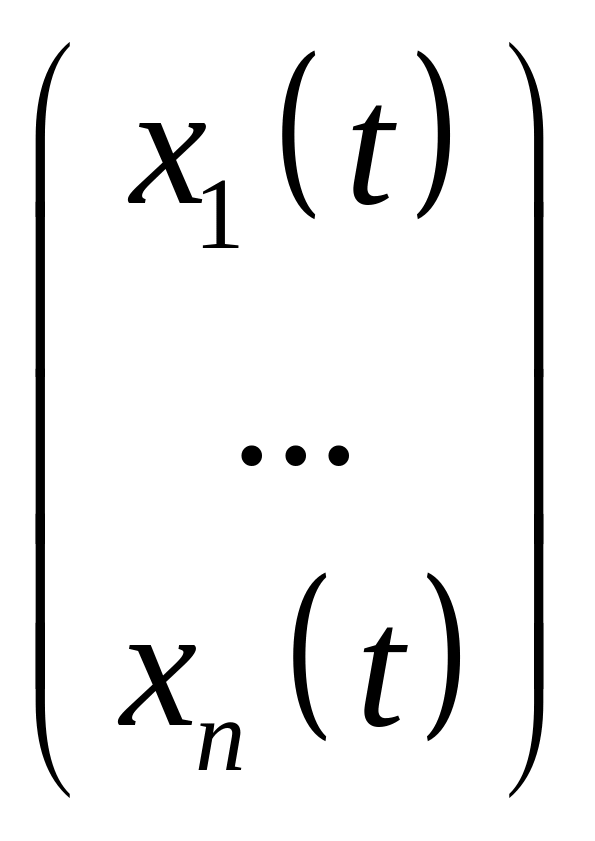= + +...+ , або

= + +...+ , де - лінійно незалежні розв’язки системи.

Надалі обмежимося лише системами двох рівнянь .

Приклад1:

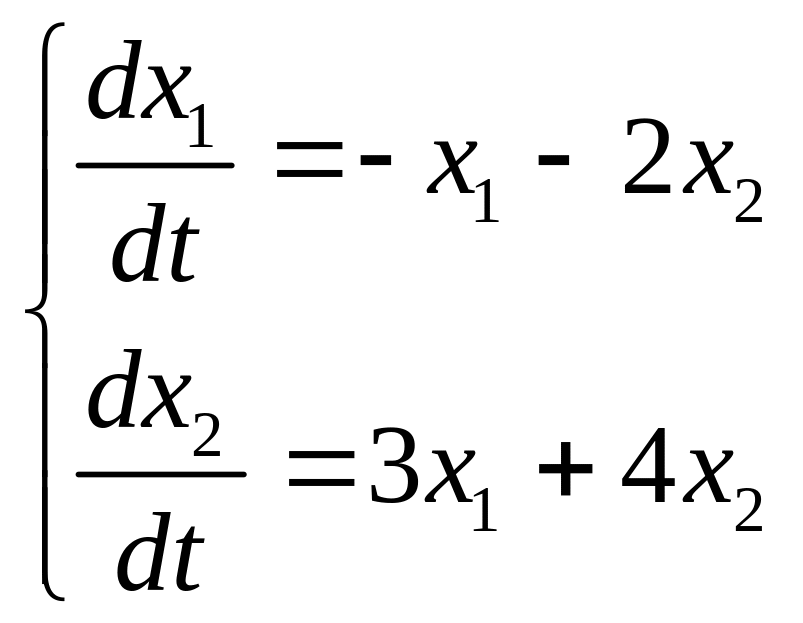. (4.6)

Характеристичне рівняння системи таке :

, або (4,7)

, яке має розв’язоки .Маємо випадок , дійсні.

Власні вектори = та = знаходимо з рівнянь :

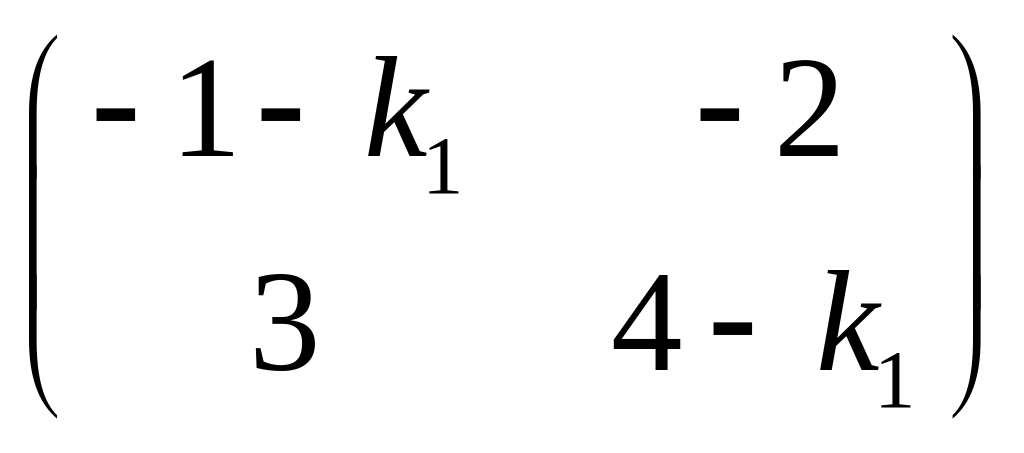=0, 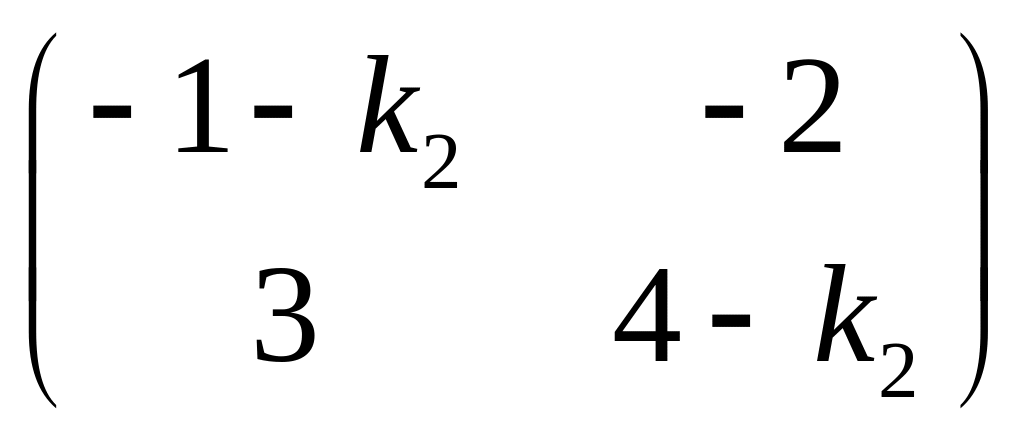=0 ,які призводять до рівнянь

та , або та .

Першу компоненту власного вектора можемо взяти рівною 1, або таку довільну, щоб усі інші компоненти були цілими числами. Маємо :

= , = і остаточно : .

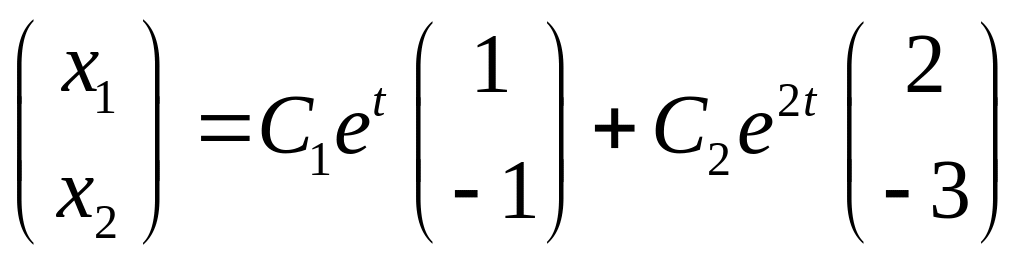Систему (4.6) , як і всяку іншу, можемо розв’язати , звівши до одного рівняння ,виключаючи усі невідомі функції (у даному випадку виключаємо лише ), крім однієї :

(4,8)

маємо з першого рівняння . Підставивши отримані вирази в друге рівняння , отримаємо рівняння другого порядку

.

Відповідним характеристичним рівнянням буде (4,7).Згідно розділу 3 маємо :

, а , підставивши в (4,8) , отримаємо : .

Приклад2:

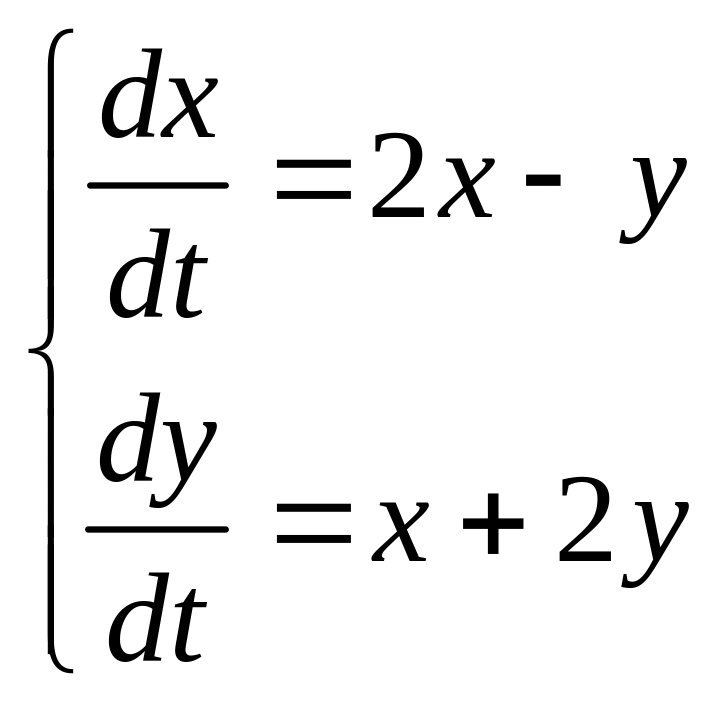(4,9).

Характеристичне рівняння системи таке :

, або

, яке має розв’язки .Маємо випадок , комплексні спряжені.

= , =0, , ,

, , = . = = є комплексним вектором , дійсна та уявна частини якого ,

являються лінійно незалежними розв’язками системи (4,9) ,а їх довільна лінійна комбінація є її загальним розв’язком:

+ .

Приклад3:

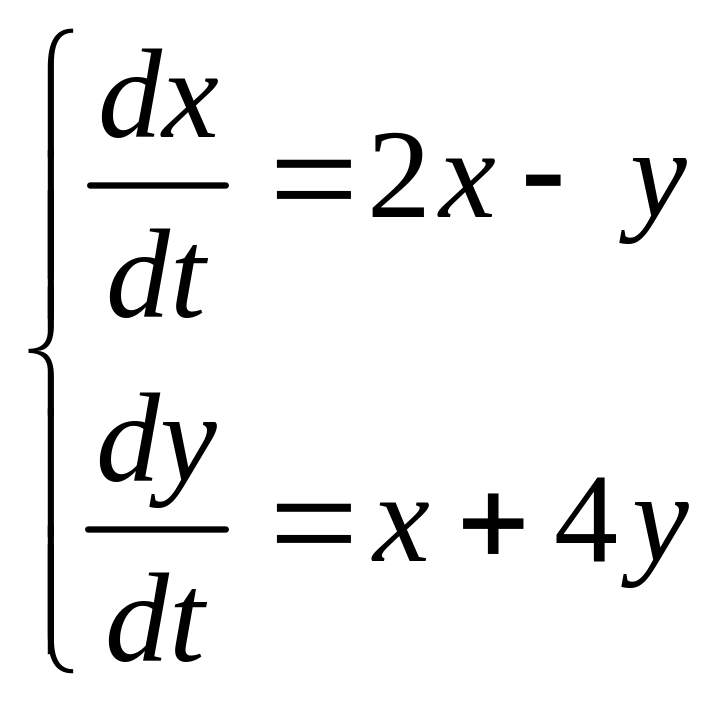(4,10).

Характеристичне рівняння системи таке :

, або , .

Маємо випадок =3, корені дійсні , співпадають.Загальний розв’язок системи (4,10) шукаємо у вигляді

(4,11).

Щоб виразити a та b через та підставимо(4,11) в (4,10) , попередньо знайшовши

. Маємо:

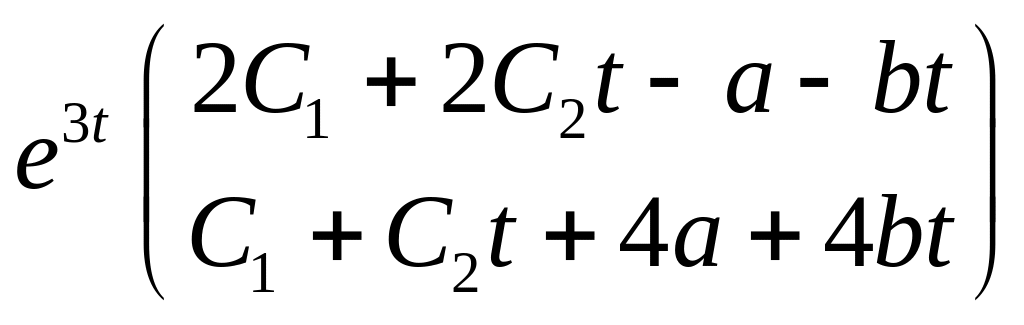= . Скоротивши на , прирівняємо або перші ,або другі рядки. Наприклад :

(4.12).

Рівність (4.12) є тотожність відносно t, значить рівні коефіцієнти при однакових

степенях t в лівій та правій її частинах:

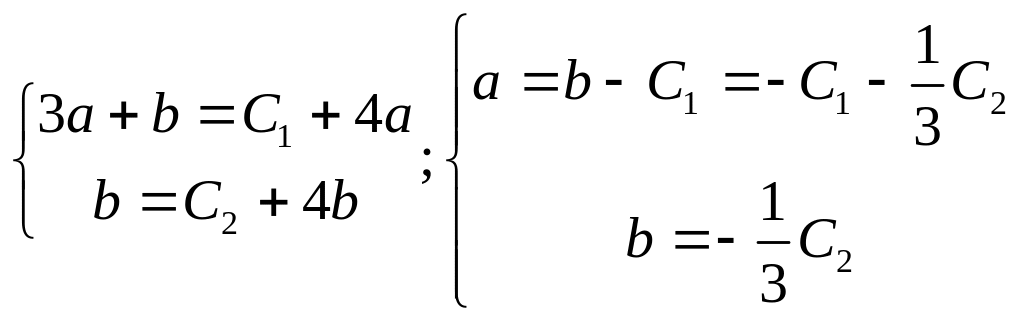
Загальний розв’язок системи (4,10) такий:

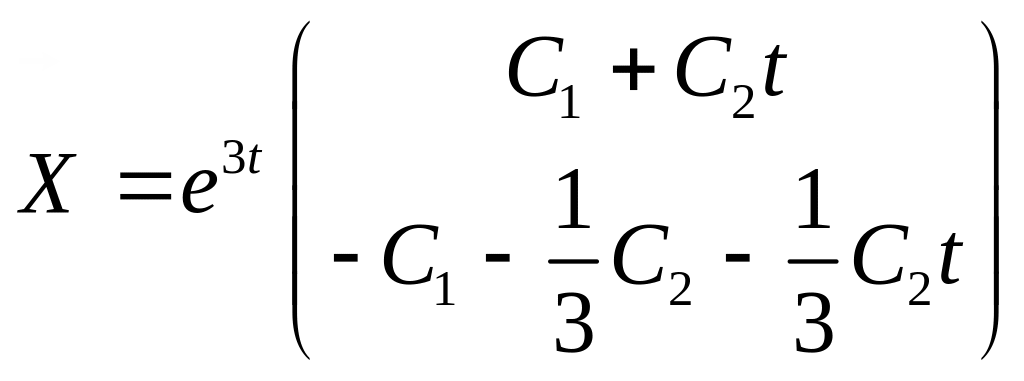
4.2 Неоднорідні системи

Загальний розв’язок неоднорідної системи шукаємо за методом Лагранжа (варіації сталих) , або, коли це можливо ,методом підбору .

Приклади.

1.

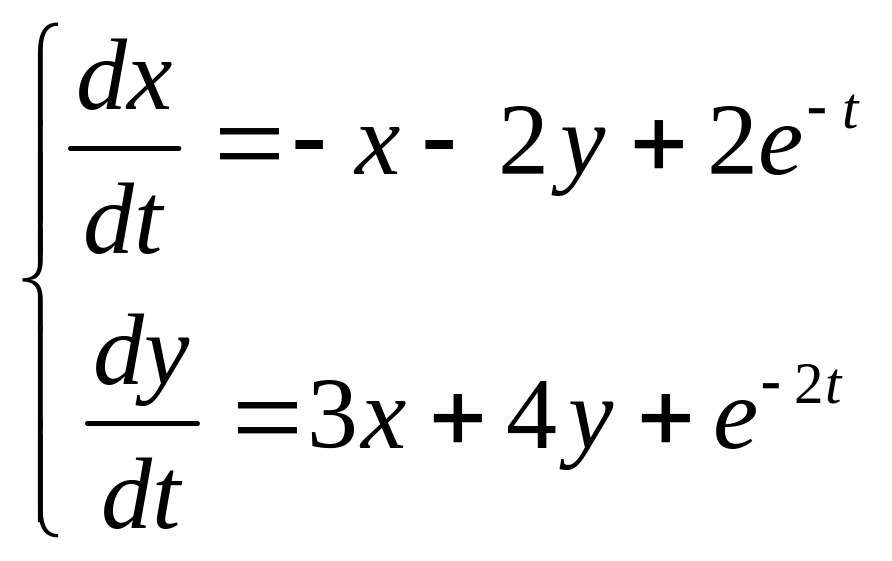. (4.13)

Відповідна однорідна система (4.6) має розв’язок

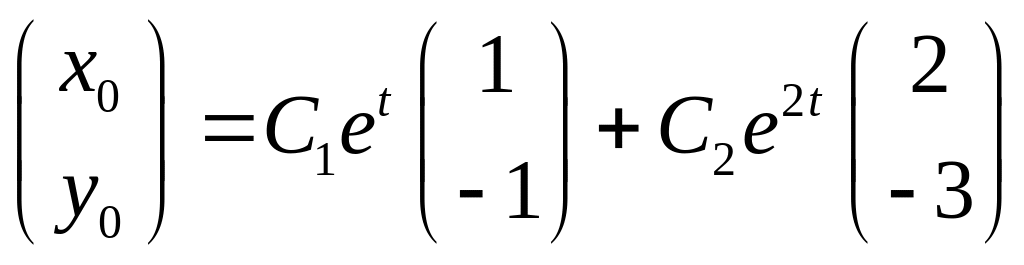.(4,14)

Розв’язок (4.13) шукаємо у вигляді

. (4.15)

та знаходимо з рівняння

,

яке зводиться до системи рівнянь

.

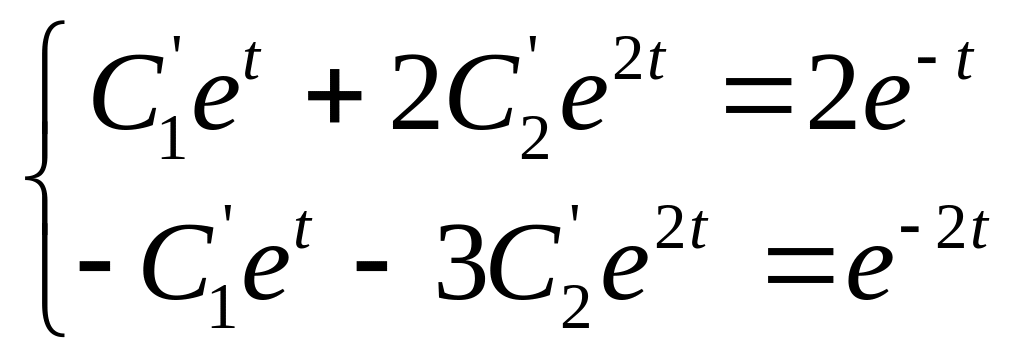Маємо: = ; = .

Після інтегрування отримаємо:

. (4.16)

Підставивши (4.16) в (4.15), маємо :

+ .

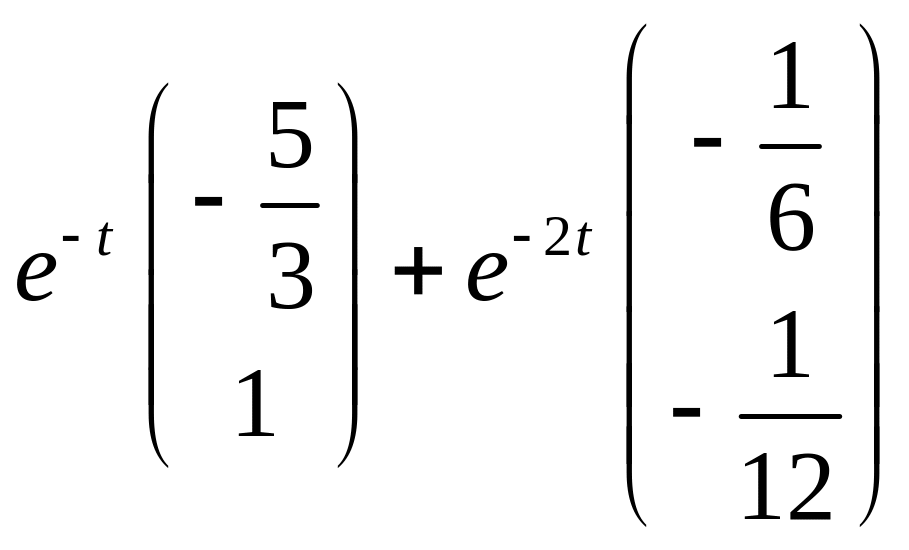Індивідуальні домашні завдання

64