
- •О.Частинним розв’язком д.Р.(2,2) наз. Розв’язок , який отримують із загального при конкретному значенні за допомогою початкових умов.
- •2.1Рівняння з відокремлюваними змінними
- •2.2 Однорідні диференціальні рівняння
- •2.3 Лінійні рівняння першого порядку
- •2.4 Рівняння Бернуллі
- •Рівняння в повних диференціалах
- •Особливі розв’язки
- •3.1 Рівняння , які допускають зниження порядку
- •3.2Лінійні рівняння о. Д.Р. Виду
- •3.3Лінійні однорідні рівняння зі сталими коефіцієнтами
- •Випадок кратних коренів
- •3.4Лінійні неоднорідні рівняння зі сталими коефіцієнтами
- •Розділ 4
2.4 Рівняння Бернуллі
О.
Д.р.
=![]() (2.4.1)
(2.4.1)
наз.д.р.
Бернуллі , якщо
![]() .
.
(При m =1 це рівняння лінійне однорідне , а при m =0 –лінйне неоднорідне , тому ці значення m виключаються )
Д.р.
Бернуллі зводиться до лінійного множенням
його на вираз
![]() ,
,
![]() :
:
![]() +
+
![]() =
=![]() ,
,
а потім заміною
![]() ,
,![]() .
.
В результаті отримаємо лінійне д.р.
![]()
![]() =
=![]() .
(2.4.2)
.
(2.4.2)
Якщо
загальним розв’язком д.р. (2.4.2) є функція
![]() , то загальним розв’язком д.р. (2.4.1) є
, то загальним розв’язком д.р. (2.4.1) є
![]() .
.
Наприклад
:
![]() .
.
Тут m=3
,1-m=-2
,
отже ,
![]() ,
,
підстановка
:
![]() ,
,
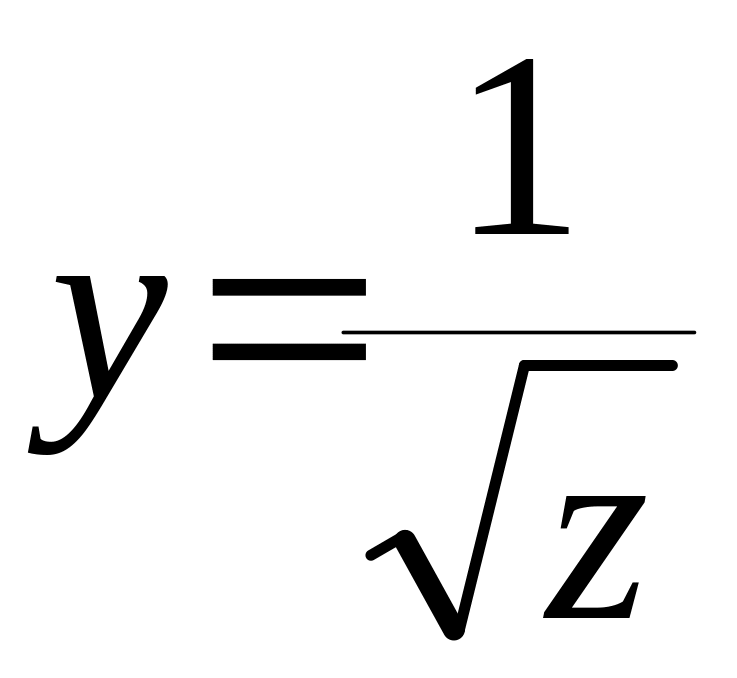 ,
,
![]() ,
,
![]() =4z-2
,
=4z-2
,
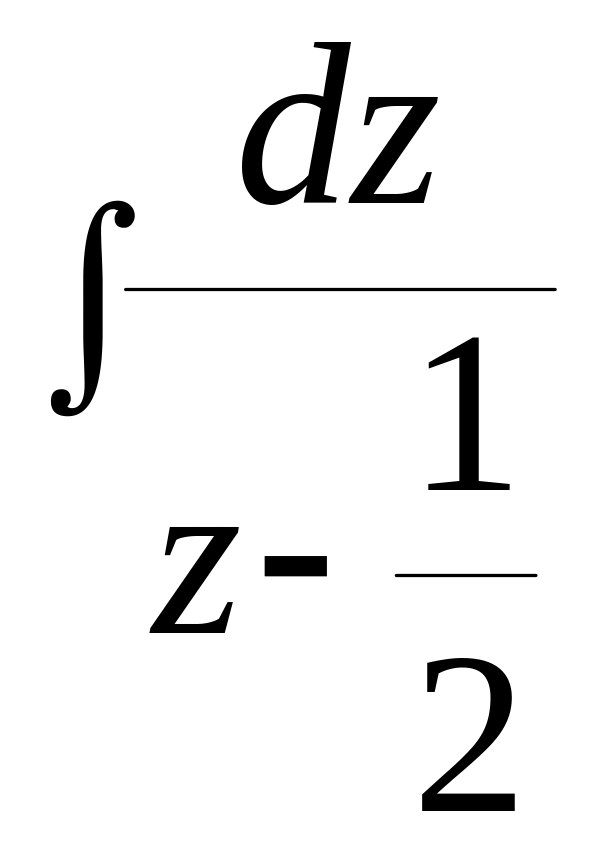 =4
=4![]() ,
,
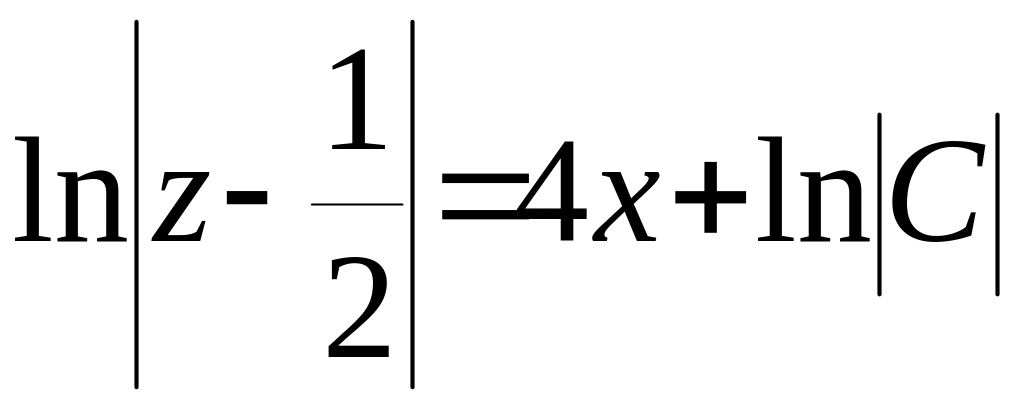 ,
,
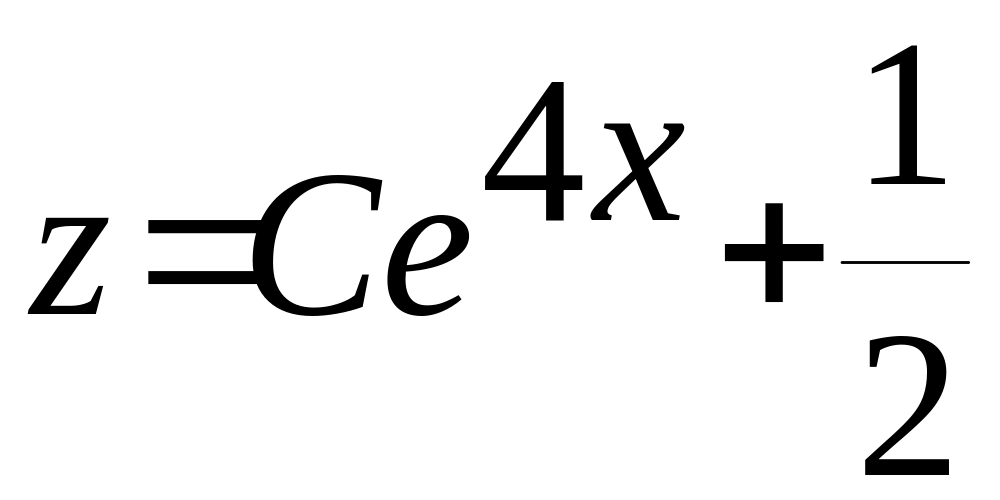 ,
,
Відповідь:
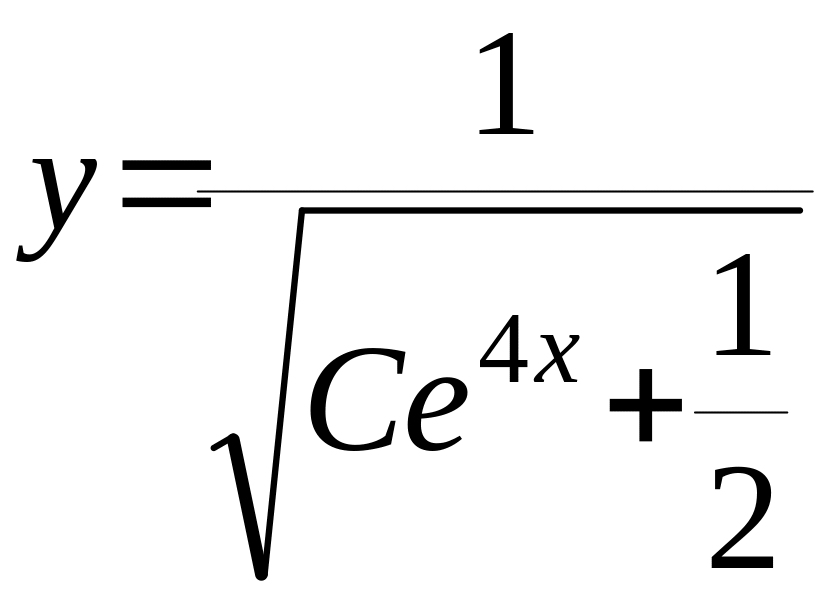
Підкреслимо , що на практиці д.р. Бернуллі простіше розв’язувати за допомогою підстановки Бернуллі .Наприклад :
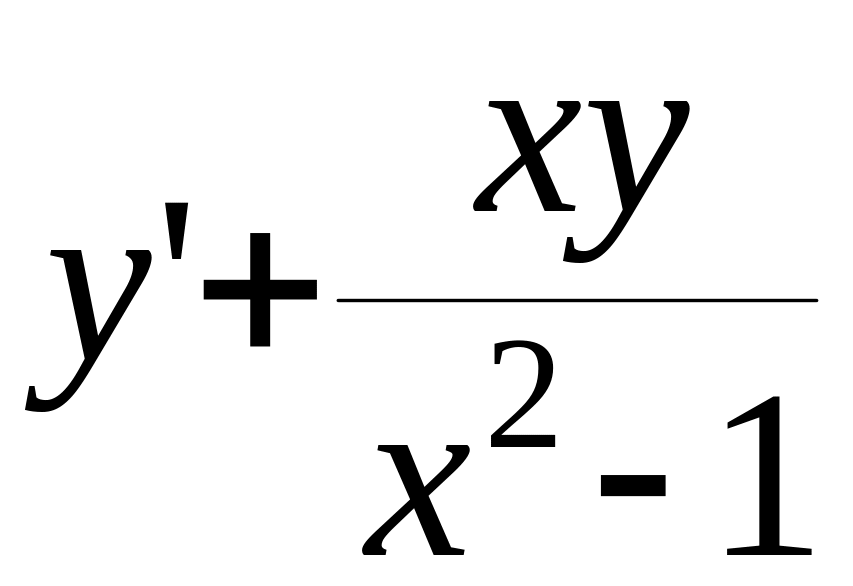 =
=
![]() ,
,
![]() ,
,
![]() +
+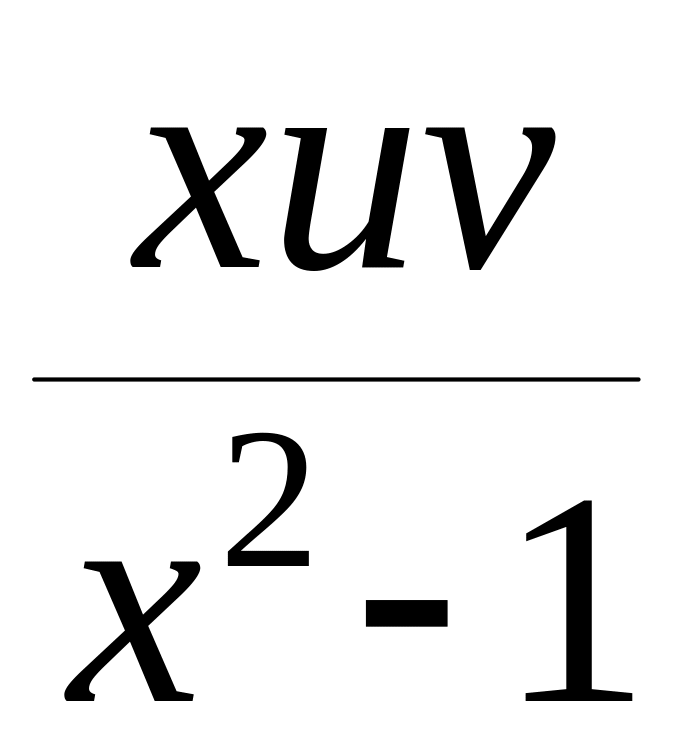 =
=
![]() ,
,
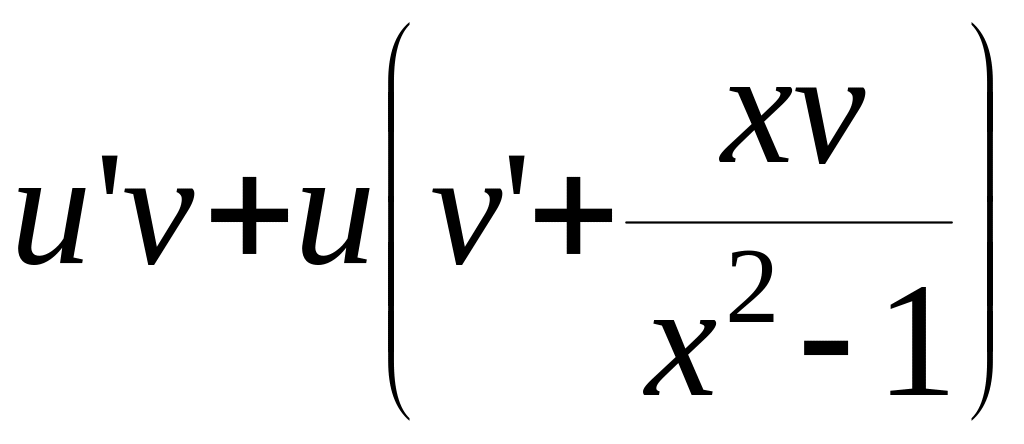 =
,
=
,
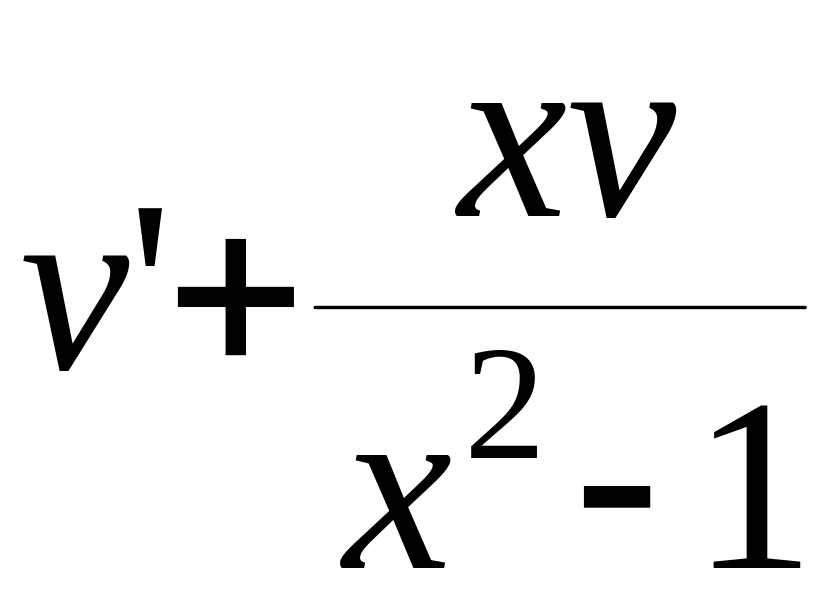 =0 ,
=
=0 ,
=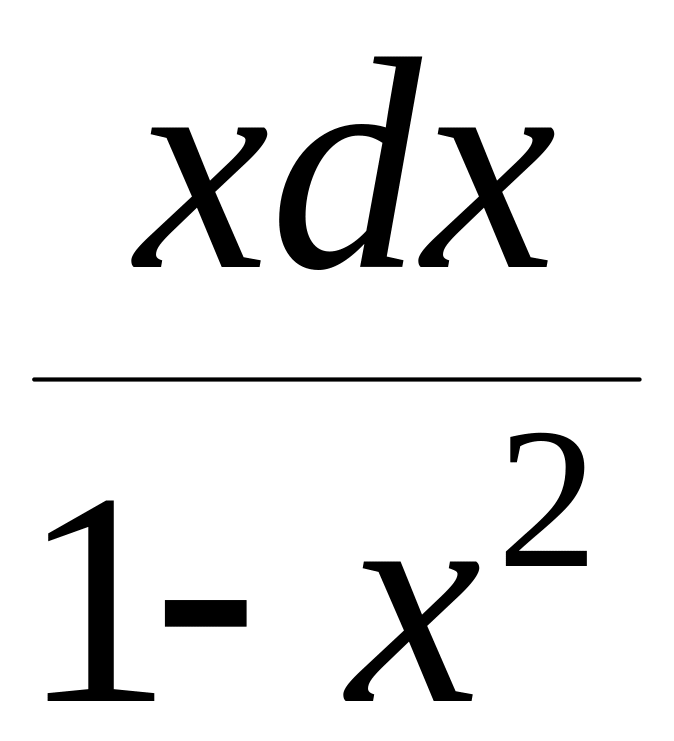 ,
,
 ,
,
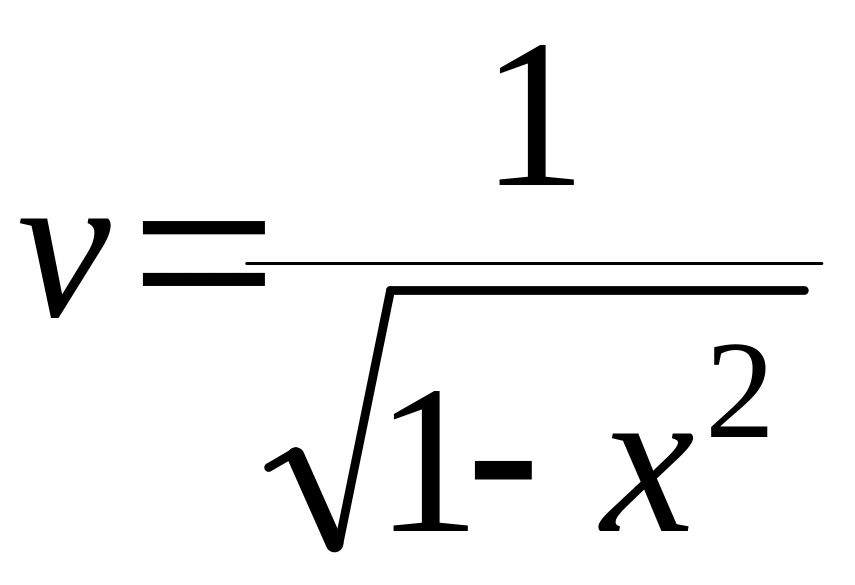 ,
,
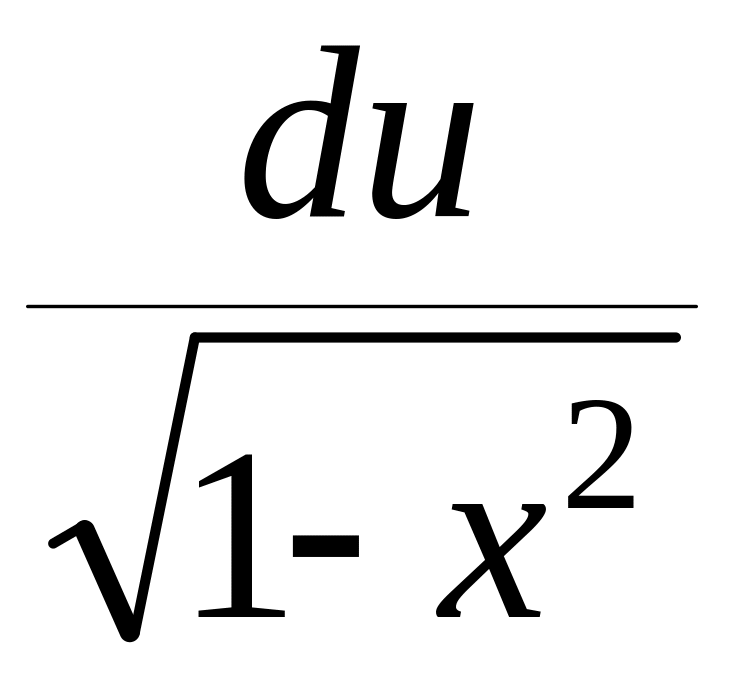 =
=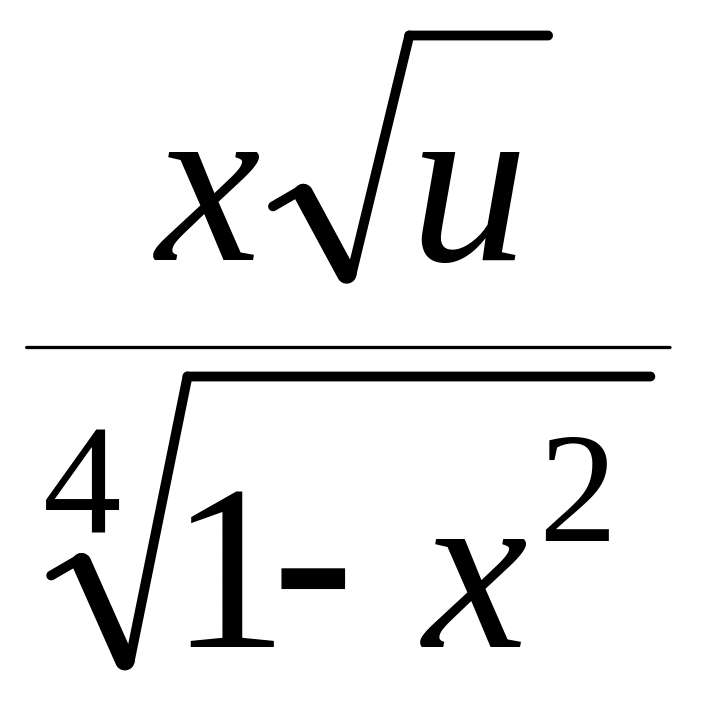 ,
,
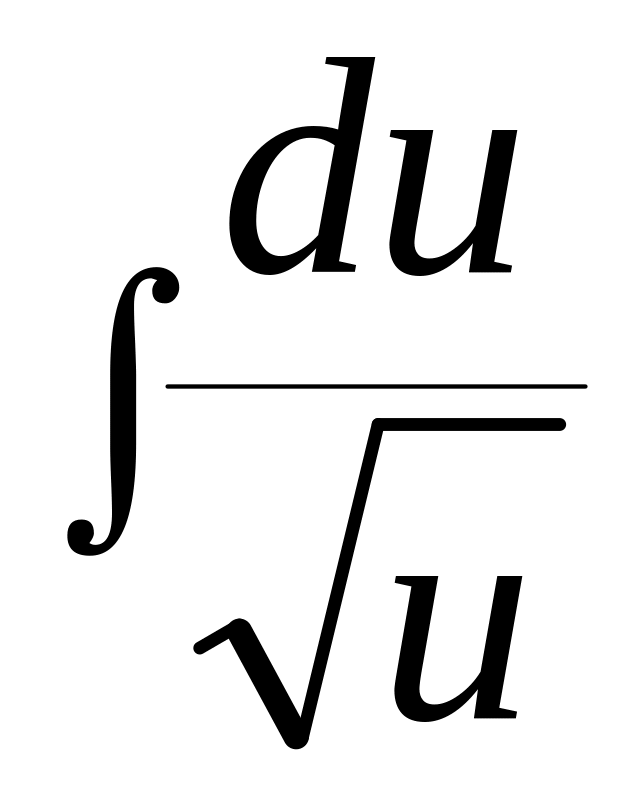 =
=
![]() ,
,
![]() = 2
= 2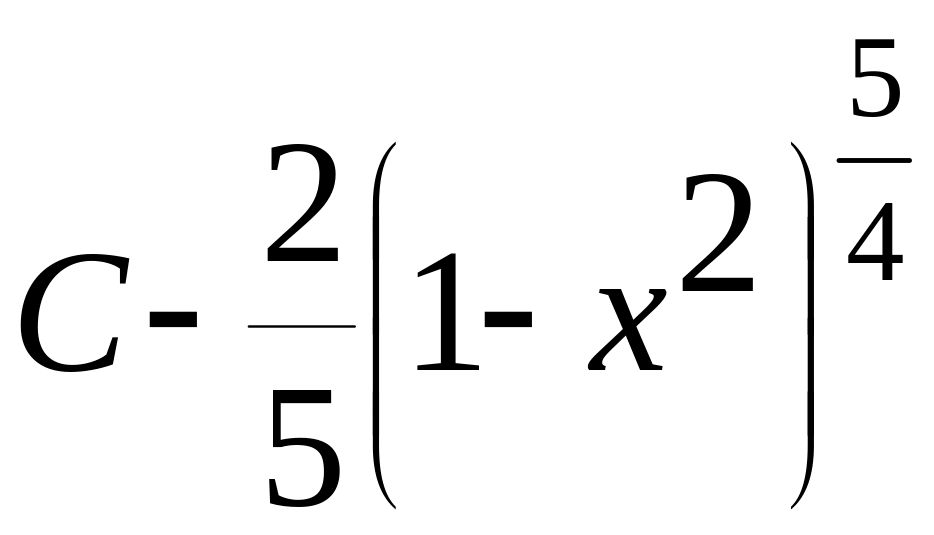 ,
,
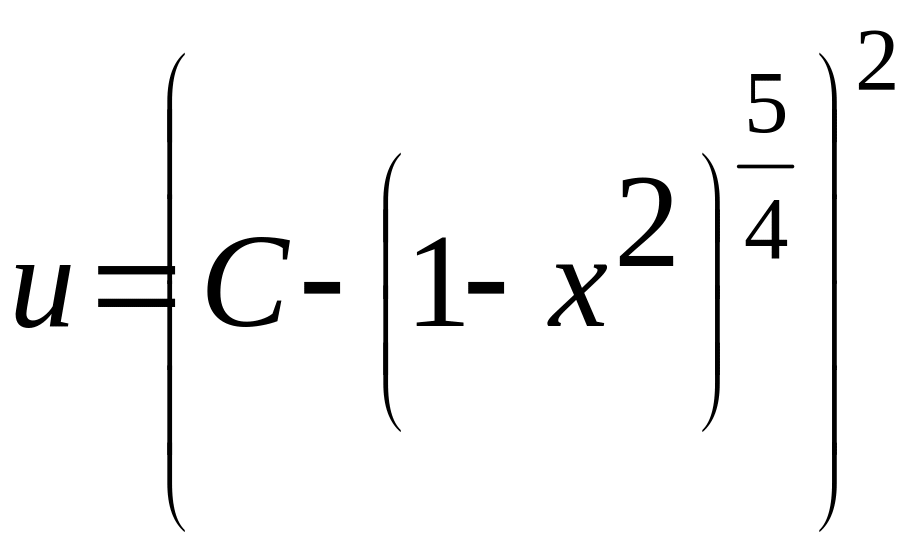 /25
,
/25
,
Відповідь:
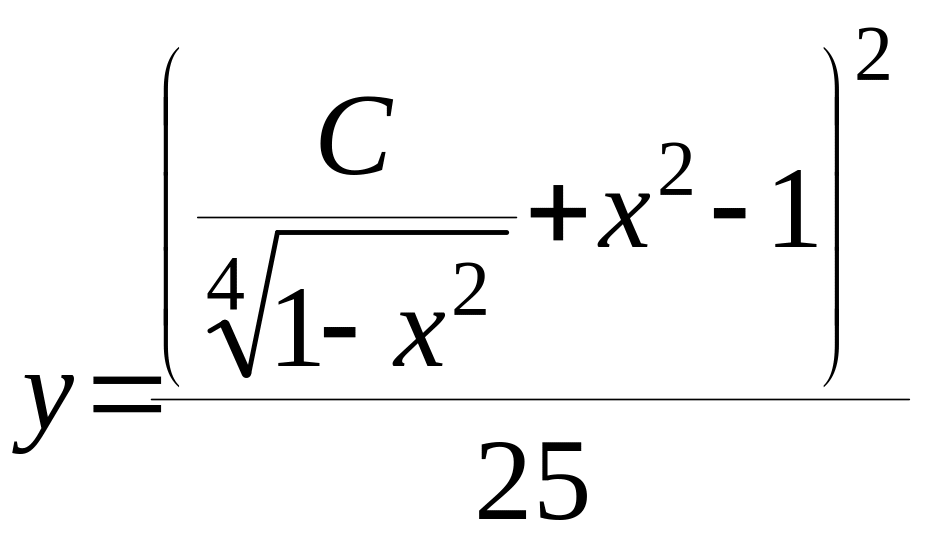 .
.
Рівняння в повних диференціалах
О.
Д.р.
![]() (2.5.1)
(2.5.1)
наз. рівнянням в повних диференціалах , якщо функції M(x,y) і N(x,y) та їх частинні похідні неперервні в заданій області і виконується рівність:
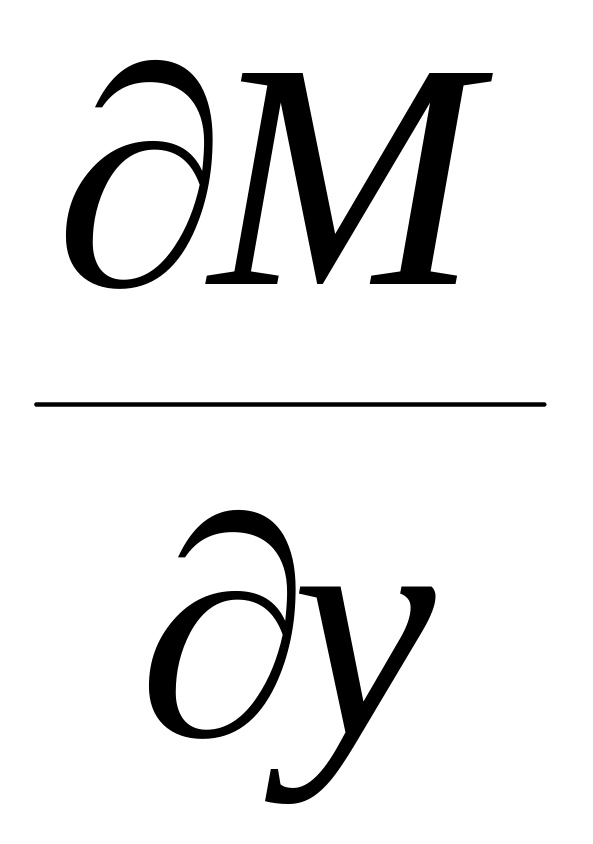 =
=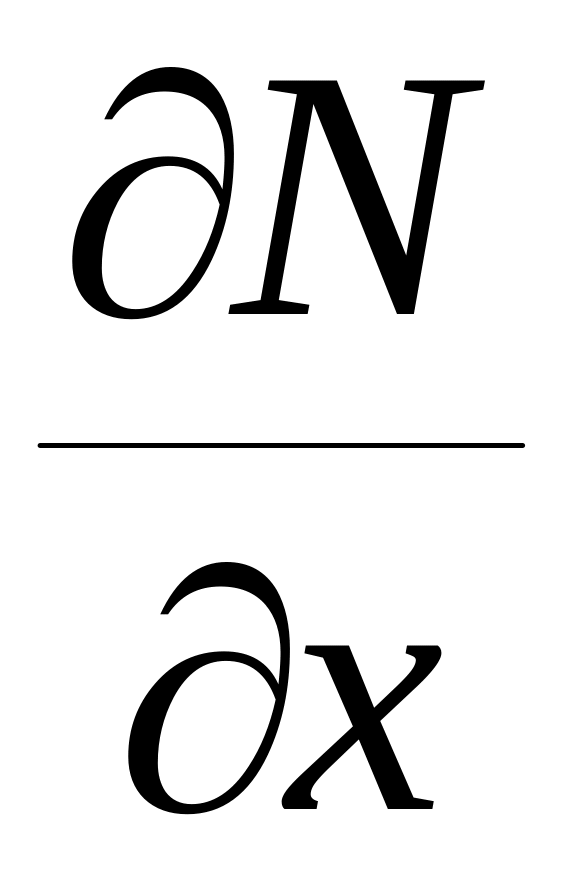 (2.5.2)
(2.5.2)
При
цьому ліва частина (2.5.1)
є
повним диференціалом деякої функції
![]() ,
тобто (2.5.1) має вигляд :
,
тобто (2.5.1) має вигляд :
![]() (2.5.3)
(2.5.3)
(
M(x,y) =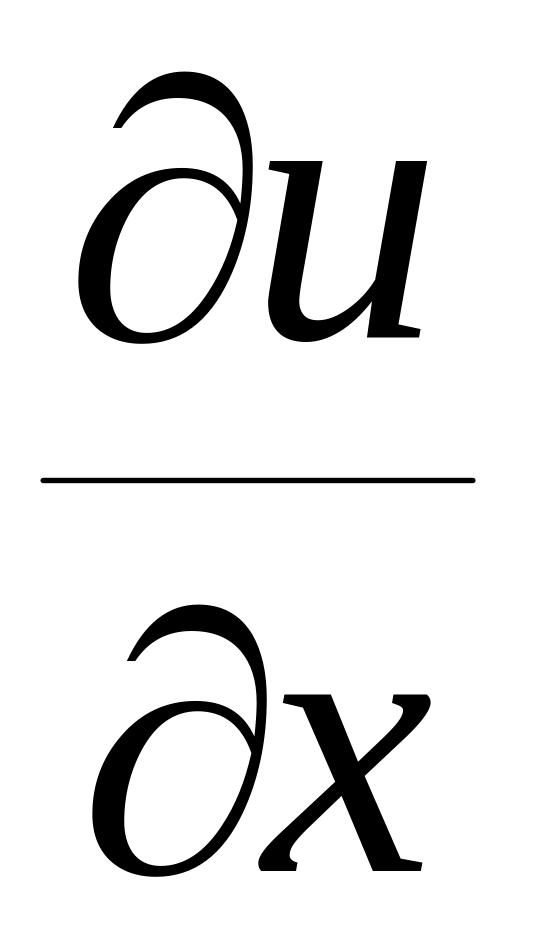 ,
N(x,y) =
,
N(x,y) =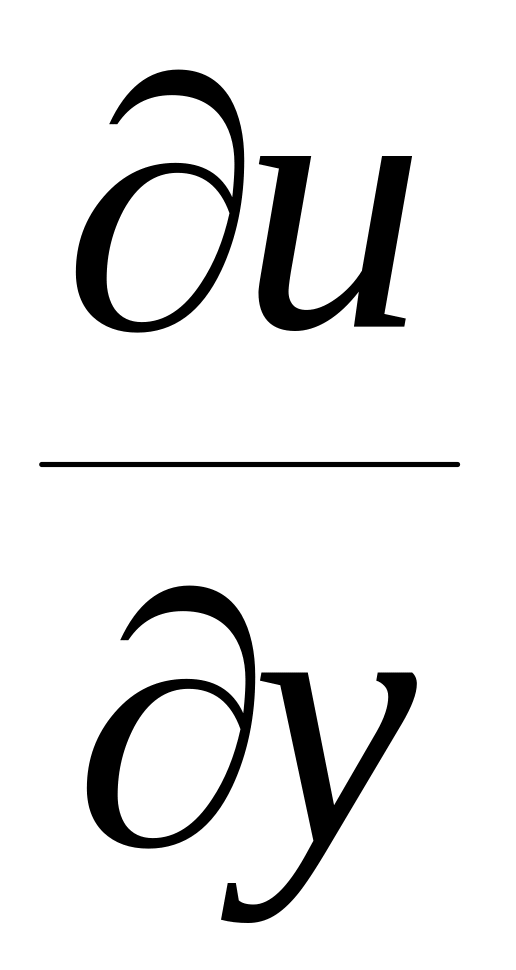 .
)
.
)
Загальний інтеграл цього д.р. такий :
=С . (2.5.4)
можемо знайти так :
=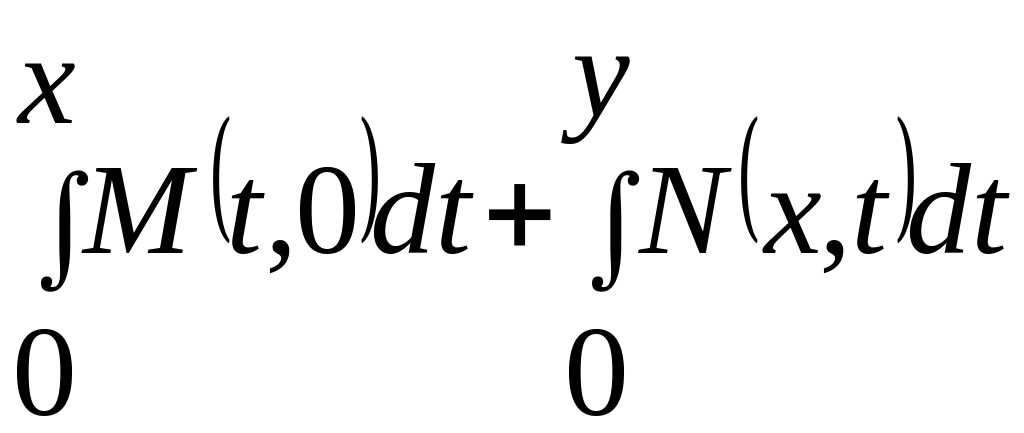 , (x=const),
або :
, (x=const),
або :
==
 ,
y=const.
,
y=const.
Наприклад:
![]() .
(2.5.5)
.
(2.5.5)
Впевнимося , що = .
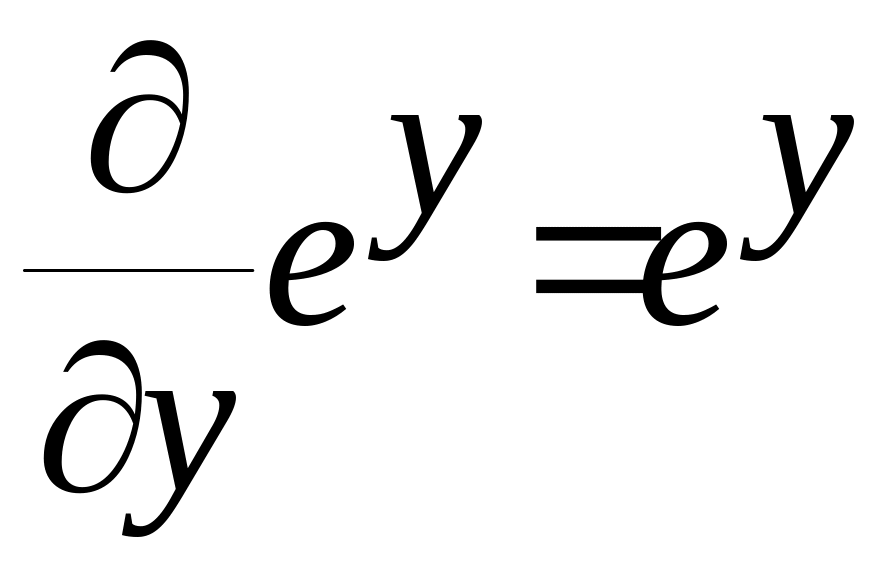 ,
,
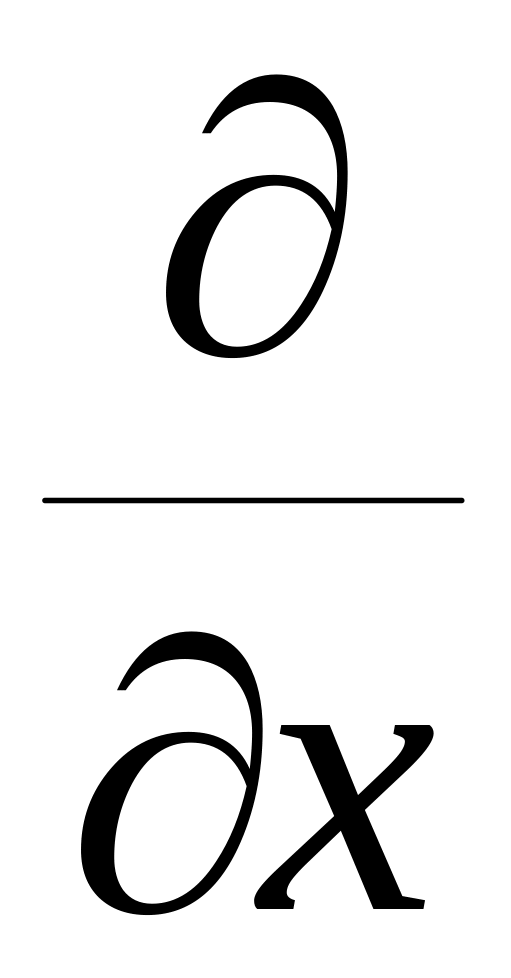
![]() =
=![]() ,
отже (2.5.5) є д.р. в повних диференціалах
.
,
отже (2.5.5) є д.р. в повних диференціалах
.
Тут
![]() .
.
= =x+
=x+![]() =
x
=
x
![]() ,
або
,
або
= =
x
.
=
x
.
Відповідь:
![]()
Ще приклад:
![]() (
(![]() )
,
)
,
(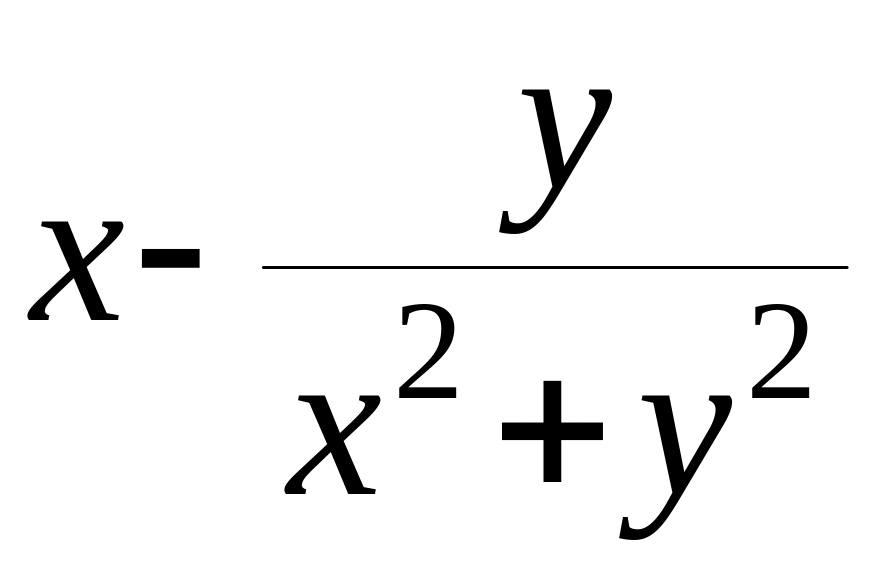 )dx
+ (
)dx
+ (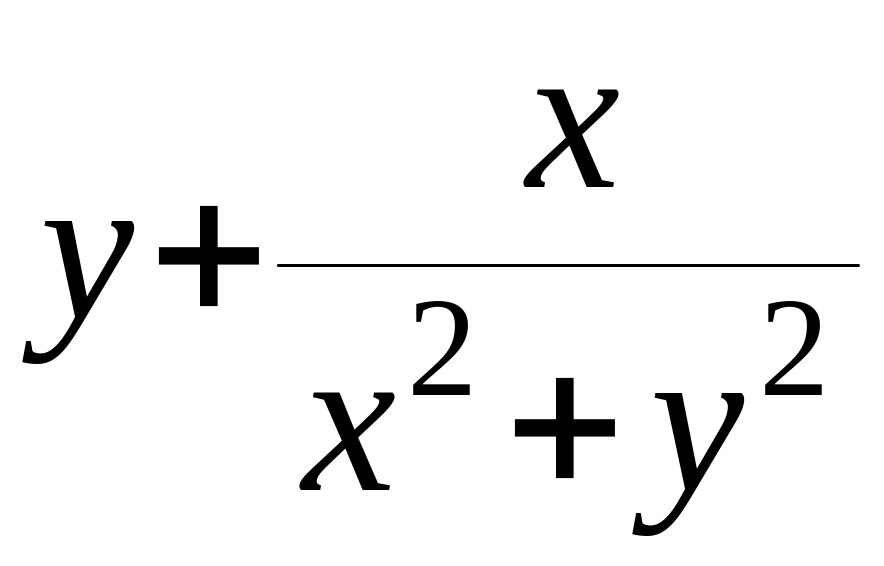 )dy=0
.
)dy=0
.
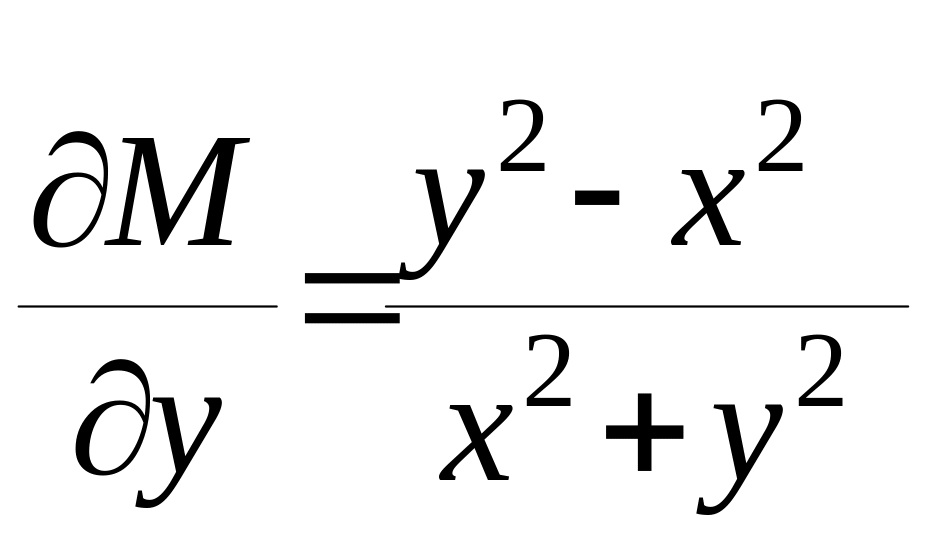 ,
=
,
=
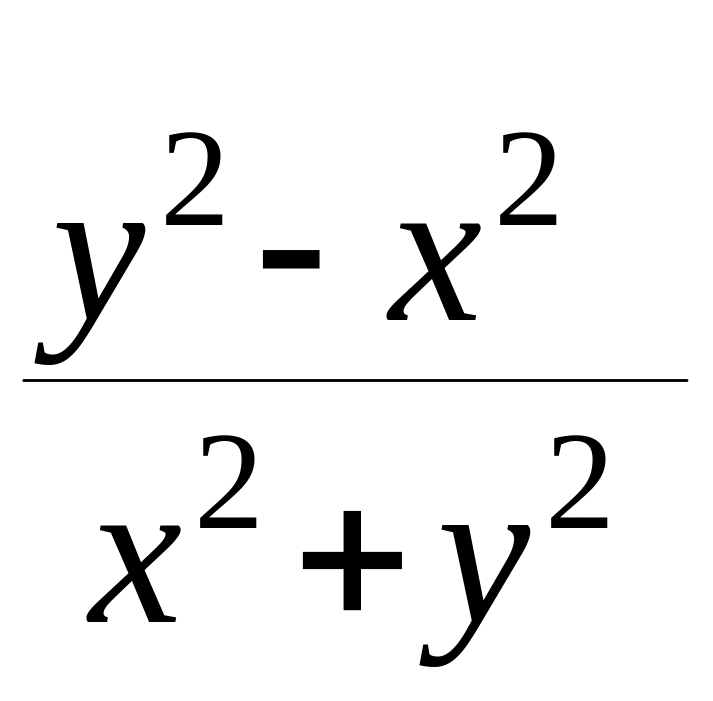 ,
отже
,
отже
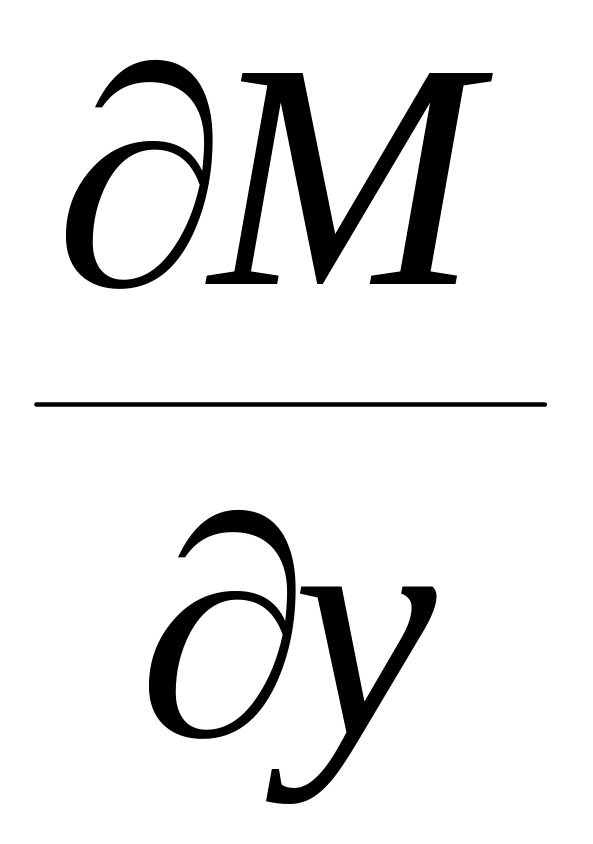 =
.
=
.
=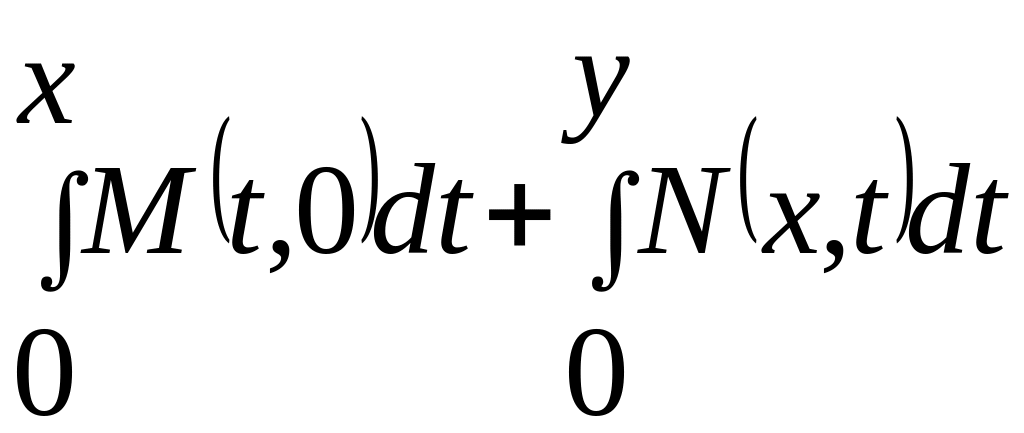 =
=
![]() tdt
+
tdt
+
![]() (
(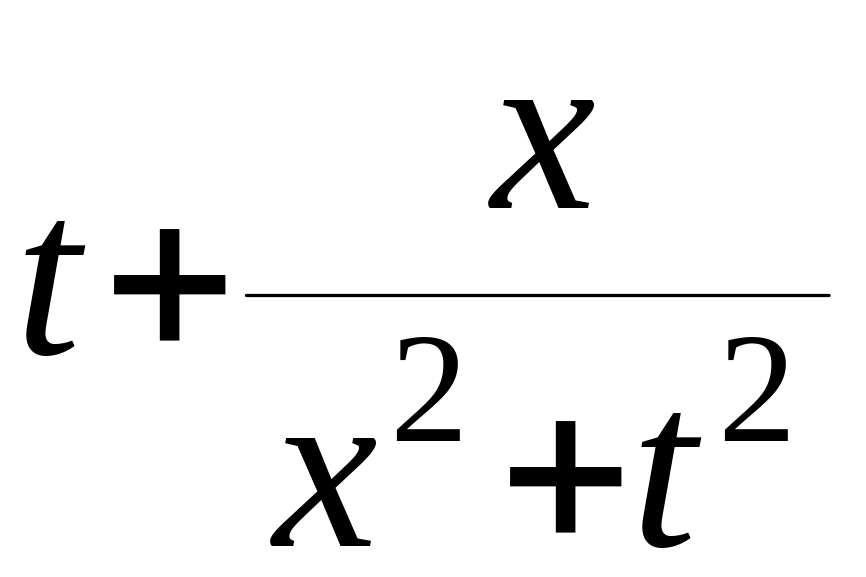 )dt
=
)dt
=
=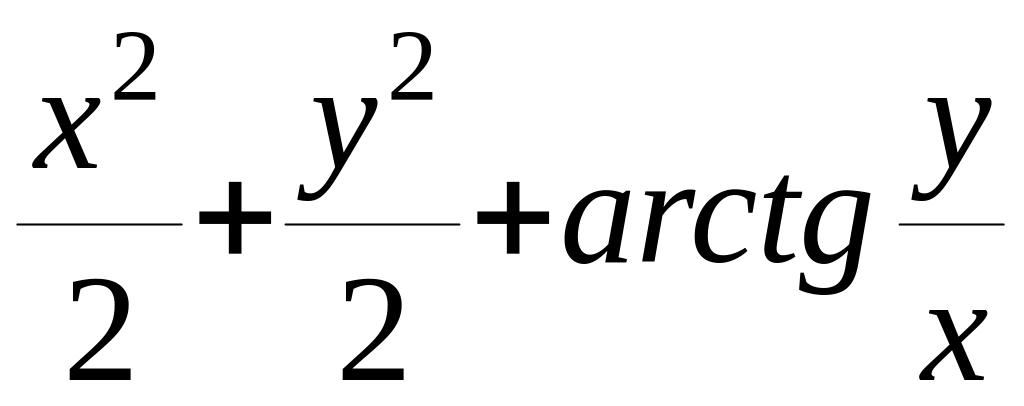 .
Відповідь:
=C.
.
Відповідь:
=C.
Якщо ліва частина д.р. не є повним
диференціалом
, то завжди існує така функція
![]() ,
,
що
![]() буде повним диференціалом .
буде повним диференціалом .
О. наз. інтегруючим множником.
Інтегруючий множник знаходять з д.р. у частинних похідних:
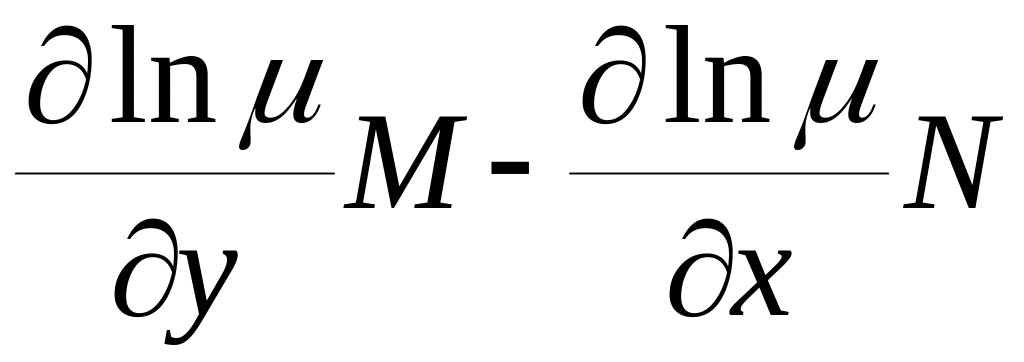 =
=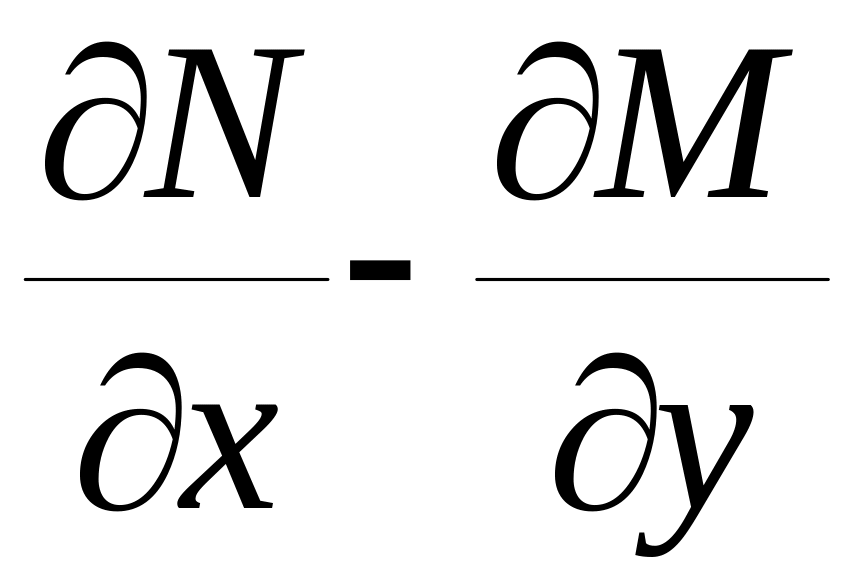 . (2.5.6)
. (2.5.6)
Якщо
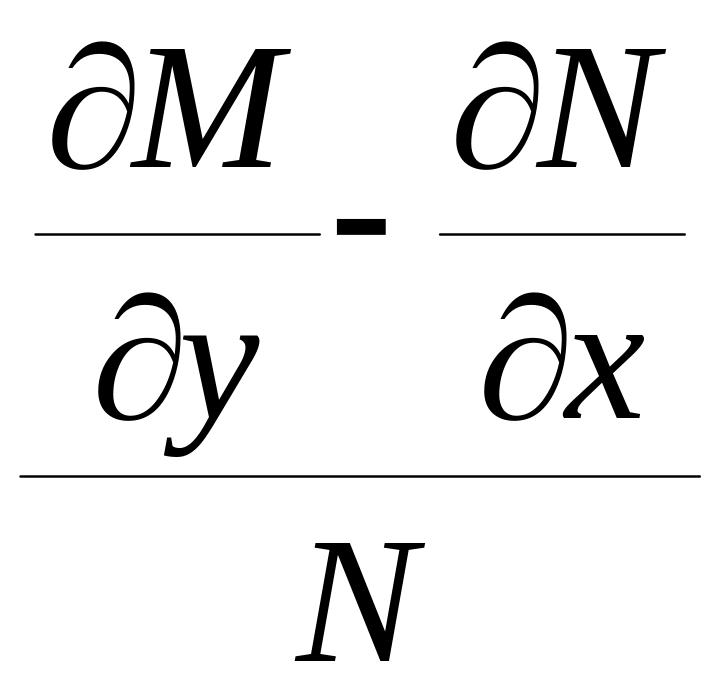 є функцією не залежною від у , то
інтегруючий множник , залежний лише від
х , існує :
є функцією не залежною від у , то
інтегруючий множник , залежний лише від
х , існує :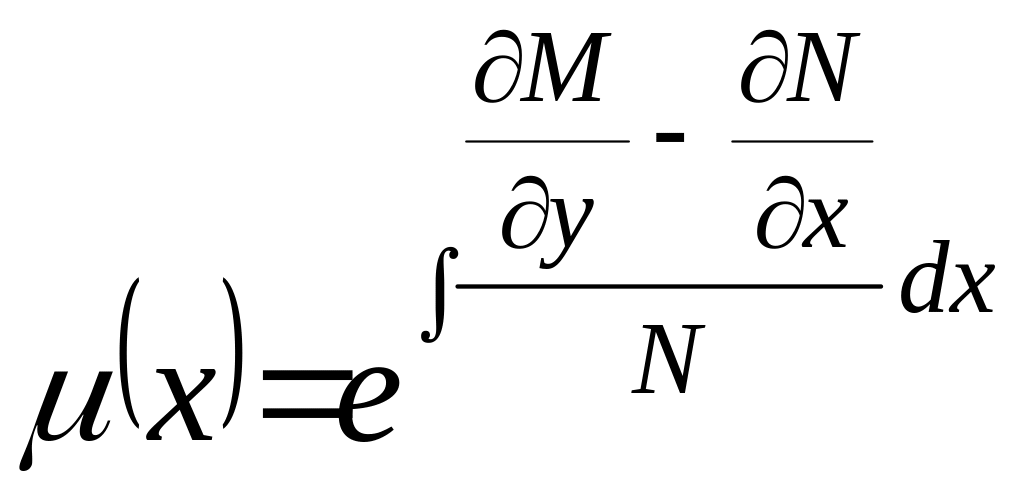 .
.
Приклад:
![]() .
(2.5.7)
.
(2.5.7)
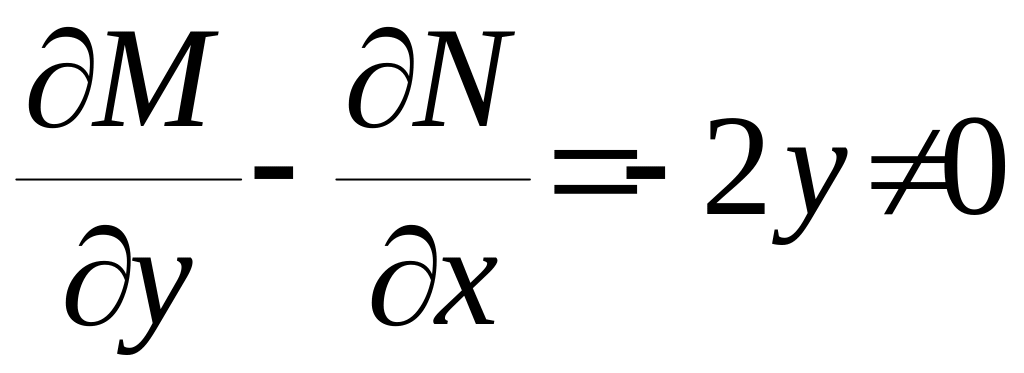 ,
отже
, треба шукати інтегруючий множник.
,
отже
, треба шукати інтегруючий множник.
(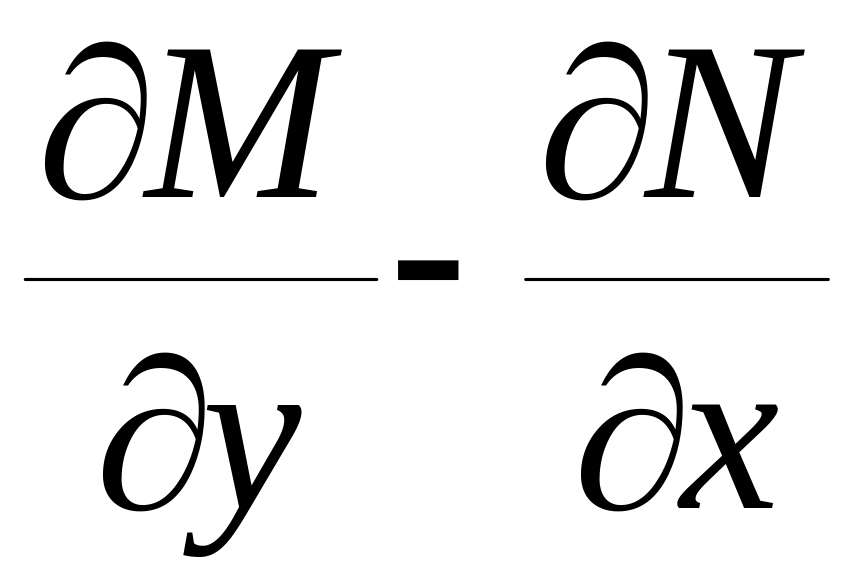 )/N
=
)/N
=
 =1
від
у не залежить , отже ,маємо :
=1
від
у не залежить , отже ,маємо :
![]()
![]()
![]() ,
тепер
M=
,
тепер
M=![]() ,N=
,N=![]() .
.
=
=
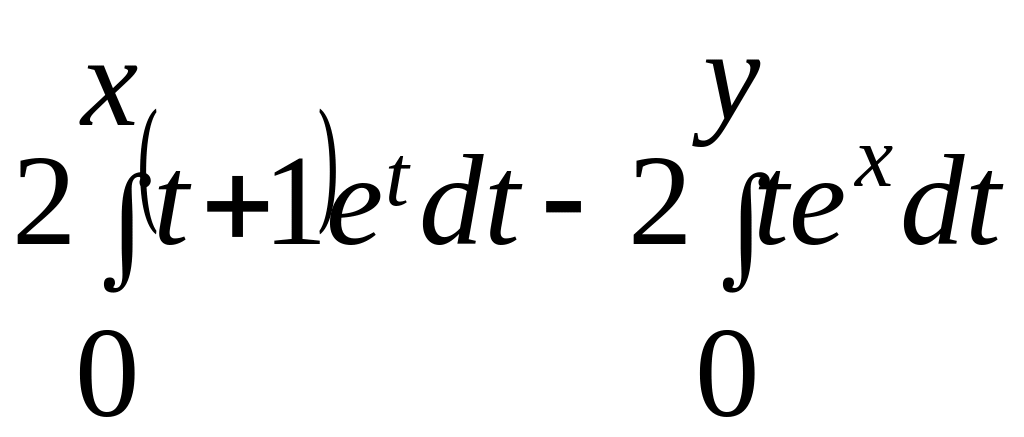 =
=![]() .
.
Відповідь: =C.
Якщо
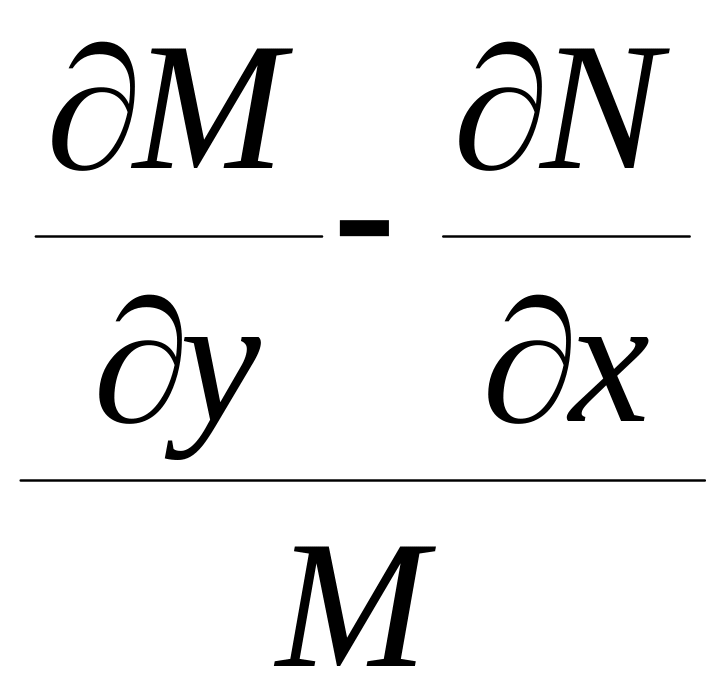 є функцією не залежною від x
, то інтегруючий множник , залежний лише
від y
, існує :
є функцією не залежною від x
, то інтегруючий множник , залежний лише
від y
, існує :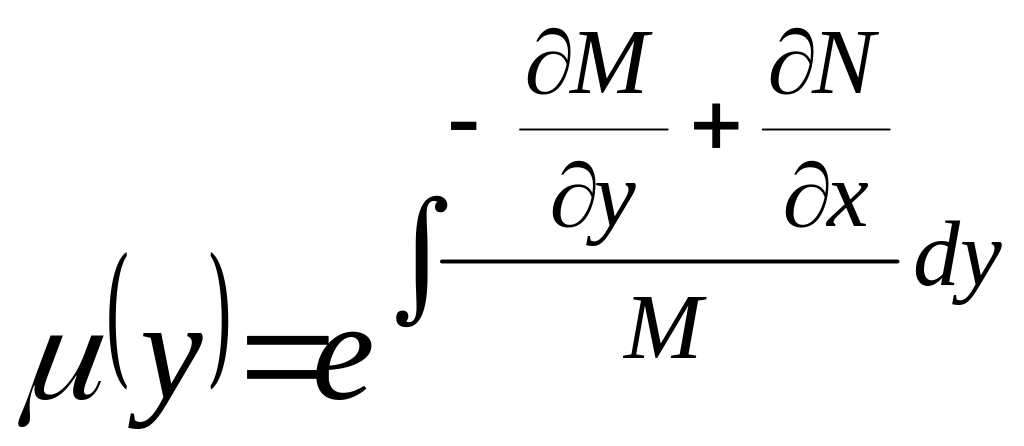 .
.
Приклад:
![]() (2.5.8)
(2.5.8)
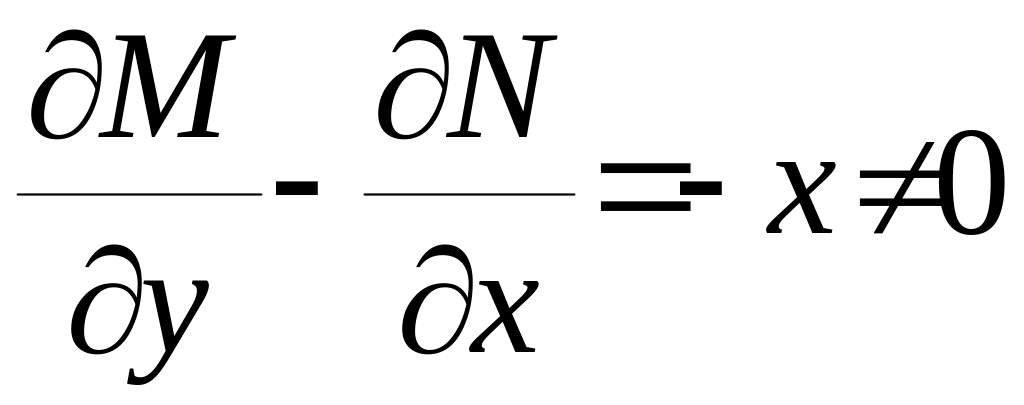 ,
отже
, треба шукати інтегруючий множник.
,
отже
, треба шукати інтегруючий множник.
(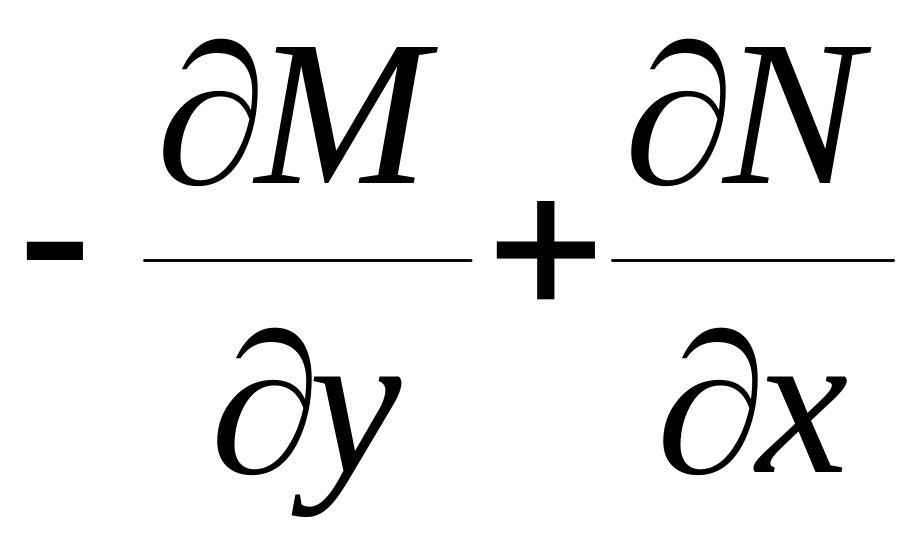 )/M
=
)/M
=
![]() від
x
не
залежить , отже ,маємо :
від
x
не
залежить , отже ,маємо :
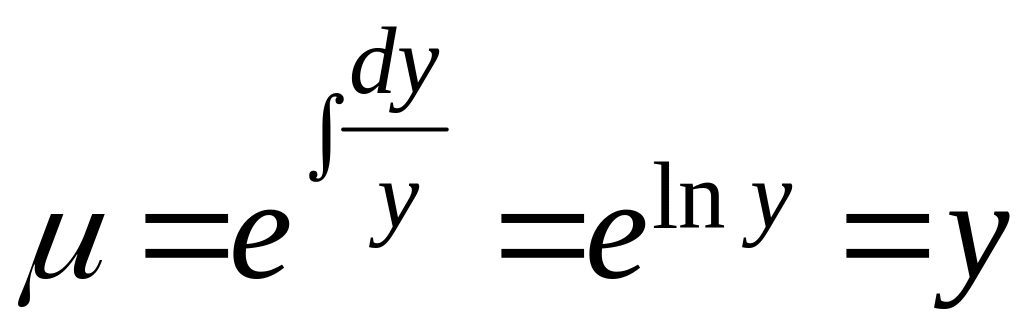 ,
(2.5.8) після
множення на
,
(2.5.8) після
множення на
![]() буде мати вид
буде мати вид
![]() ,
,
=
=
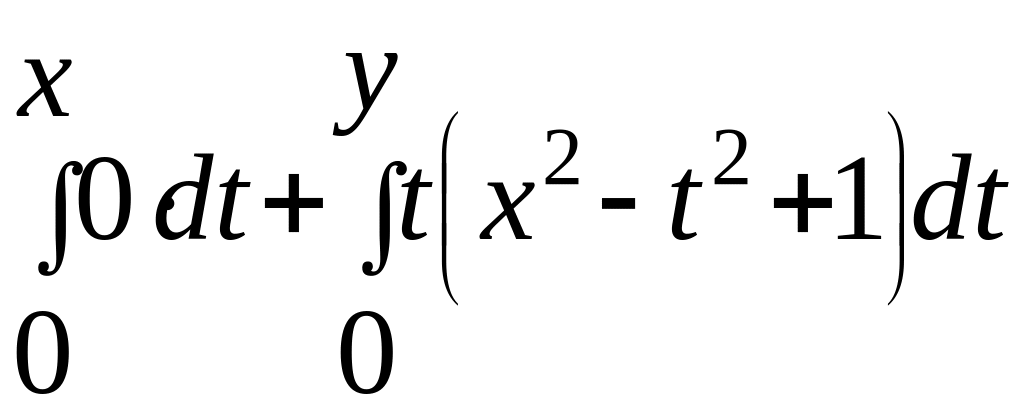 =
=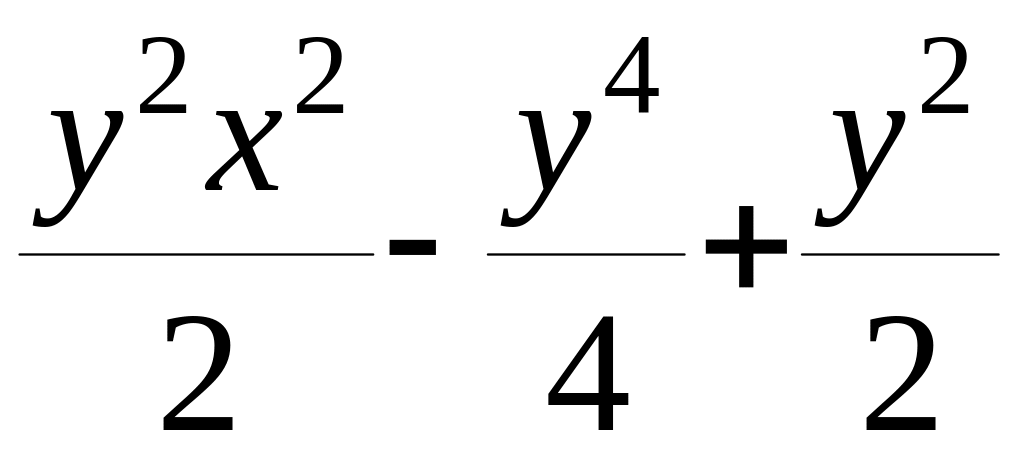 .
.
Відповідь:
![]()
З (2.5.6) можливо знайти умови існування інтегруючих множників виду
 тощо.
тощо.
