2.3 Лінійні рівняння першого порядку

О. Д.р. наз. лінійним,якщо невідома функція та її похідні вхоять до рівняння лише в першому степені.

Лінійне д .р. першого порядку має вигляд :

= , (2.3.1)

де P(x) та Q(x) задані неперервні в деякому проміжку функції від х.

Наприклад .

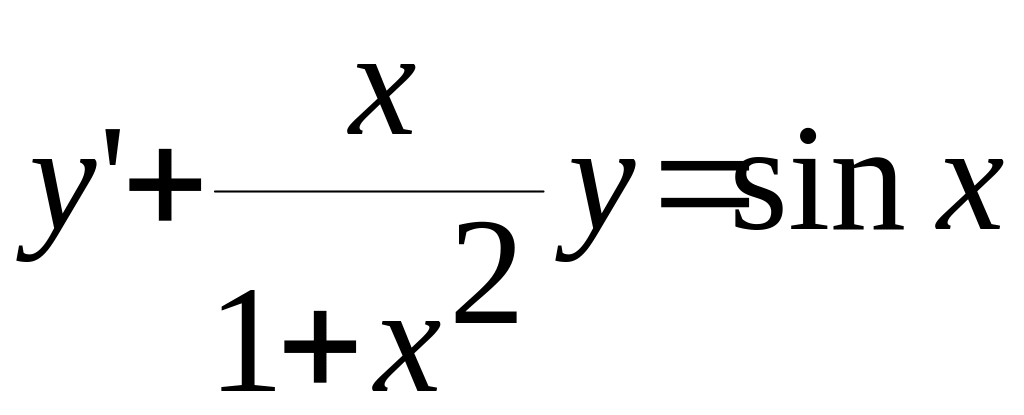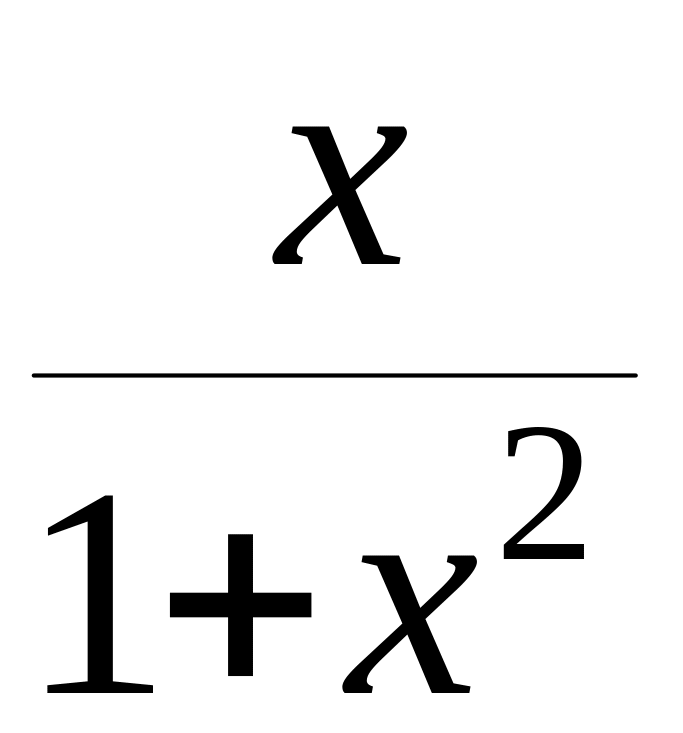Тут (х)= , Q(x)=sinx .

Якщо Q(x)0, то (2.3.1) має вигляд

=0 (2.3.2)

і наз лінійним однорідним рівнянням, а якщо Q(x) 0 , то лінійним неоднорідним . Д.р. (2.3.2) є д.р. з відокремлюваними змінними.

Розглянемо два способи розв’язування д.р. (2.3.1).

Метод варіації довільної сталої (метод Лагранжа)

Д.р. (2.3.2) є д.р. з відокремлюваними змінними:

= , = , ,

що є загальним розв’язком д.р. (2.3.2).

Загальний розв’язок д.р. (2.3.1) шукаємо у вигляді

(2.3.3)

де , нова невідома функція. Підставляємо та - до (2.3.1):

- +

+ = ,

= ,

= ,

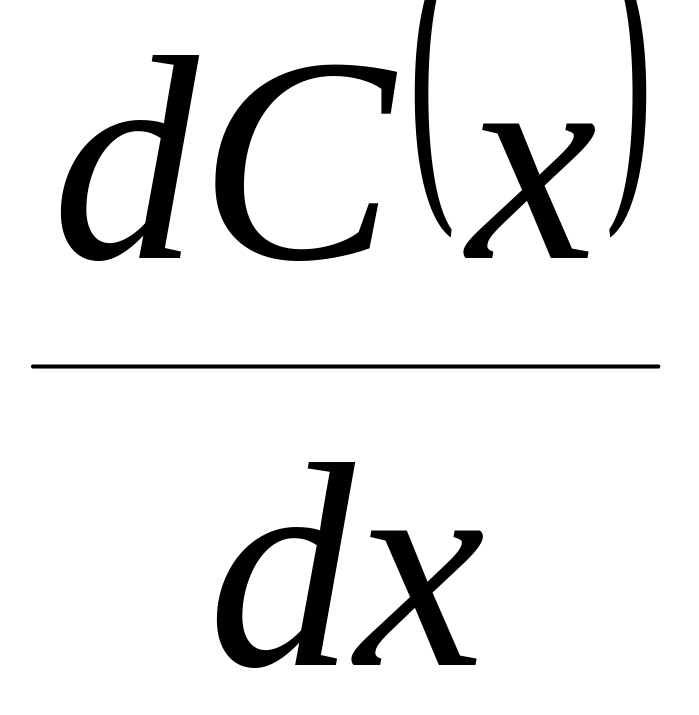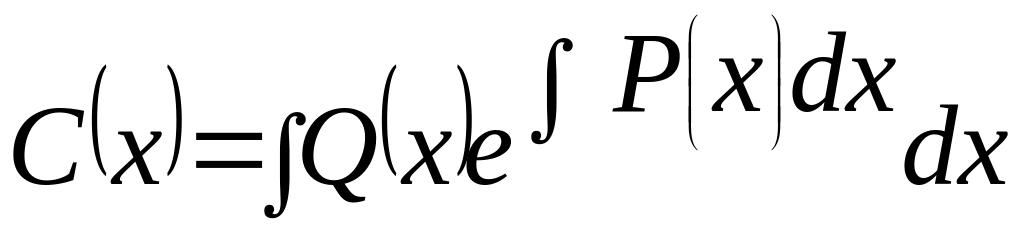+ , де -

довільна стала .

Підставимо до (2.3.3) і матимемо загальний розв’язок д.р. (2.3.1) у вигляді:

+

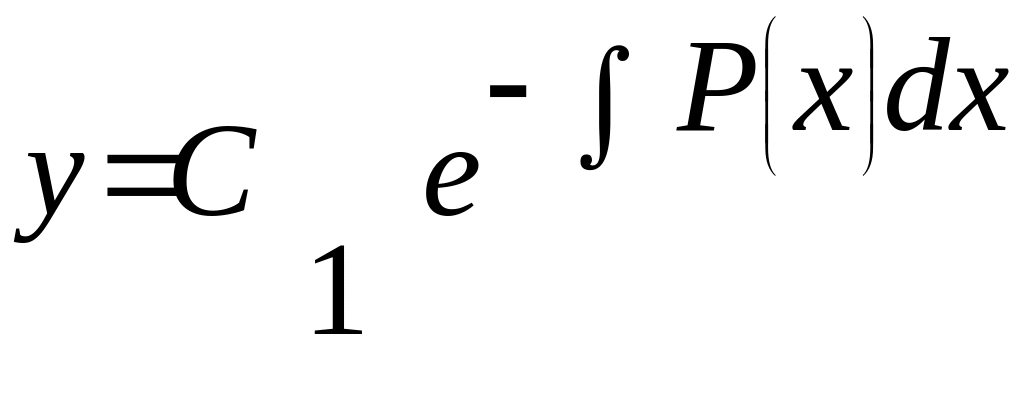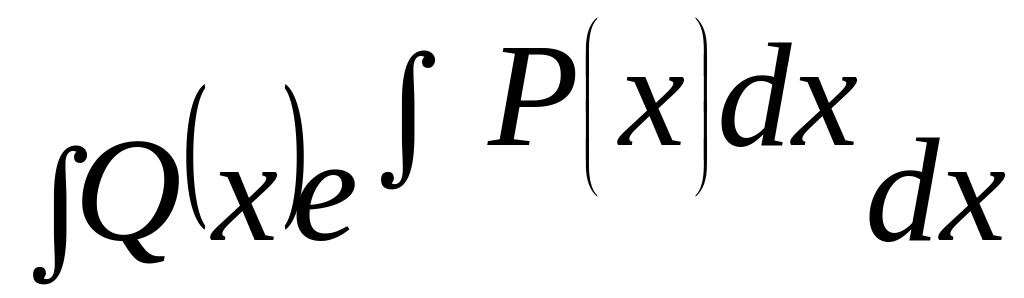+ (2.3.4)

З (2.3.4) видно , що загальний розв’язок неоднорідного лінійного

д.р. дорівнює сумі загального розв’язку відповідного однорідного

лінійного д.р.( ) та частинного розв’язку

( ) неоднорідного лінійного д.р.

Покажемо усе це на конкретному прикладі:

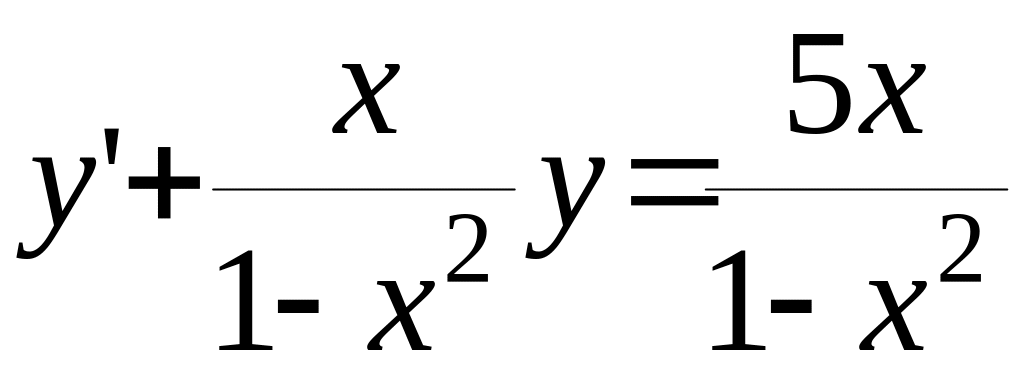(2.3.5)

Відповідне однорідне лінійе д.р. буде :

, (2.3.6)

= , = ,

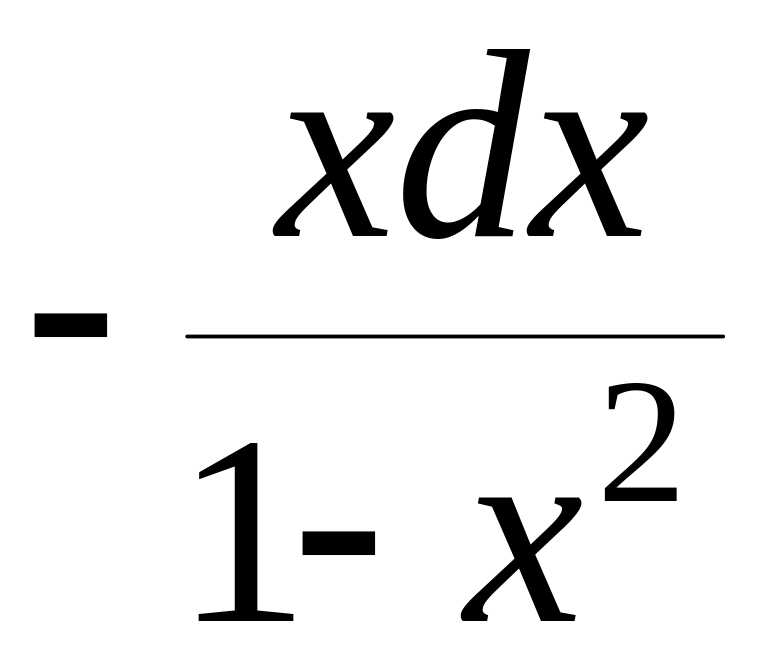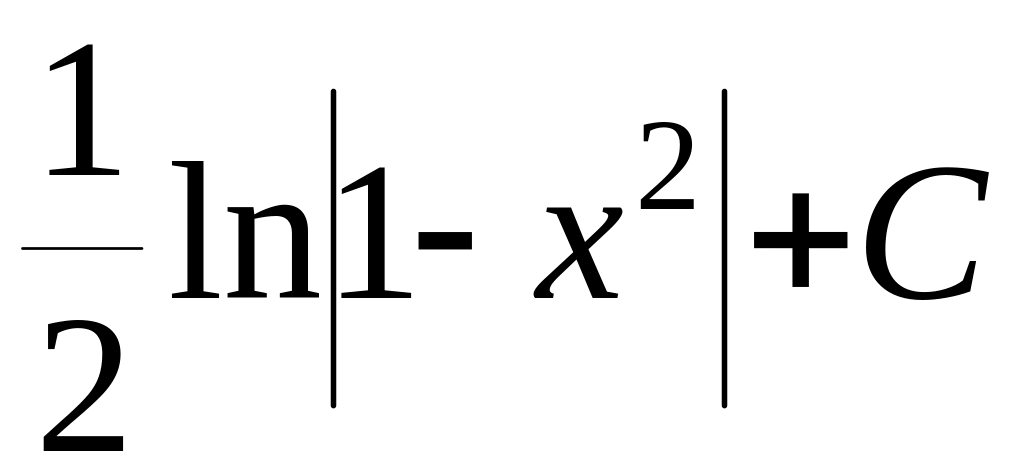, Відповідь: , що є загальним розв’язком д.р. (2.3.6).

Підставимо y в д.р. (2.3.5) , вважаючи , що С є функція від х та , врахувавши , що тоді - :

- + = ,

= , ,

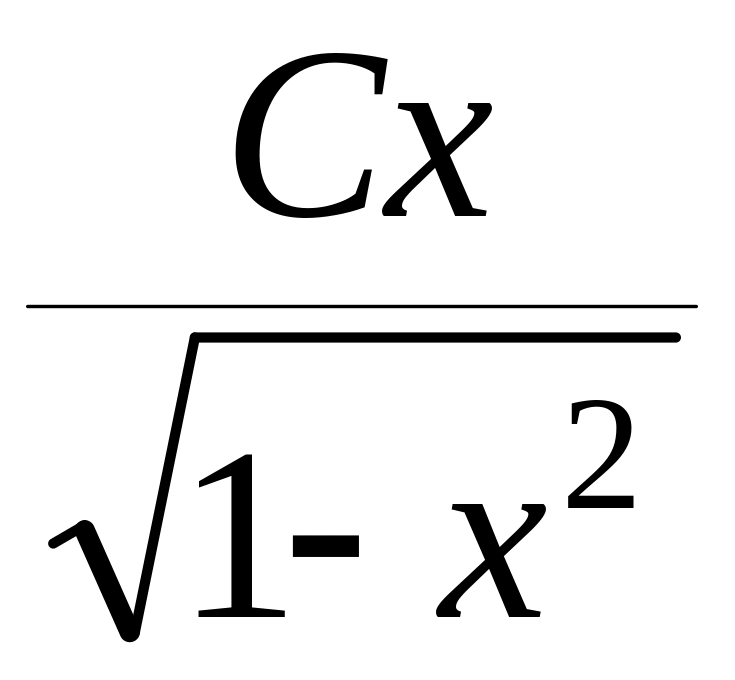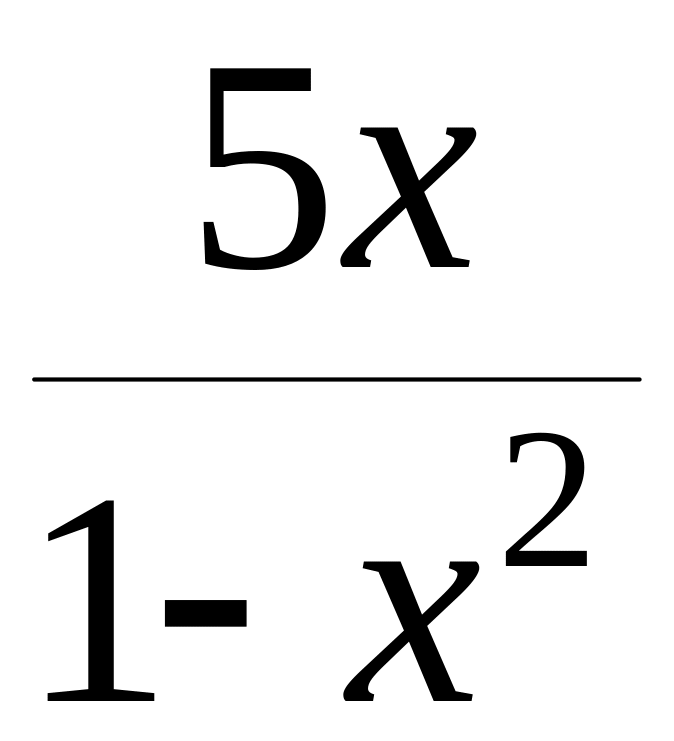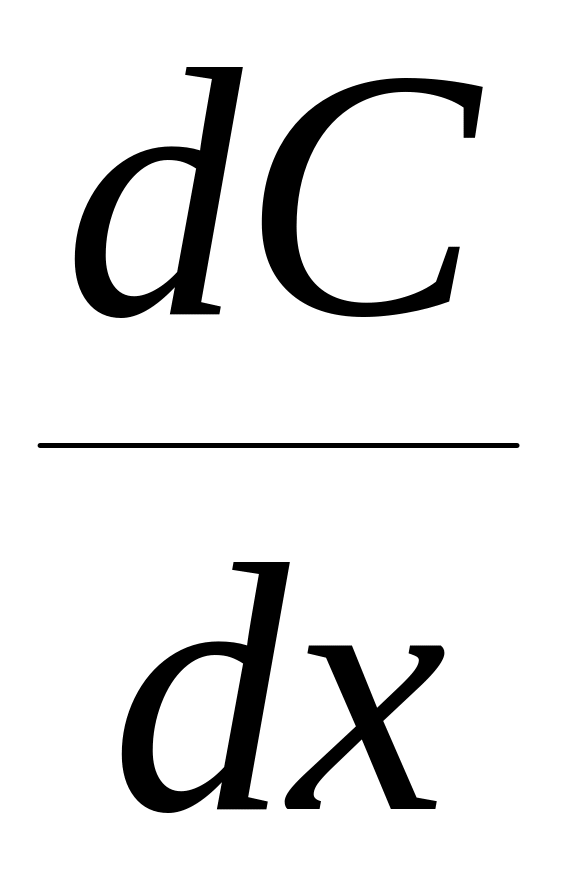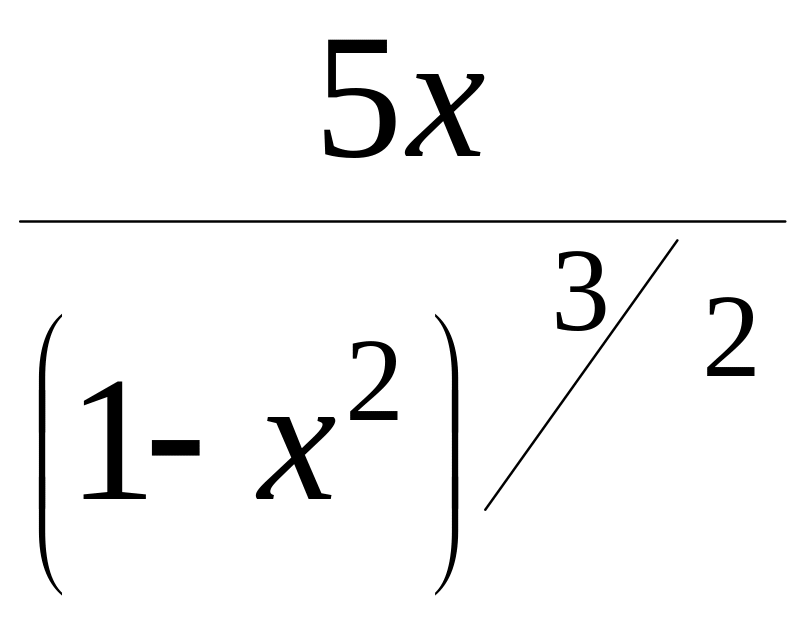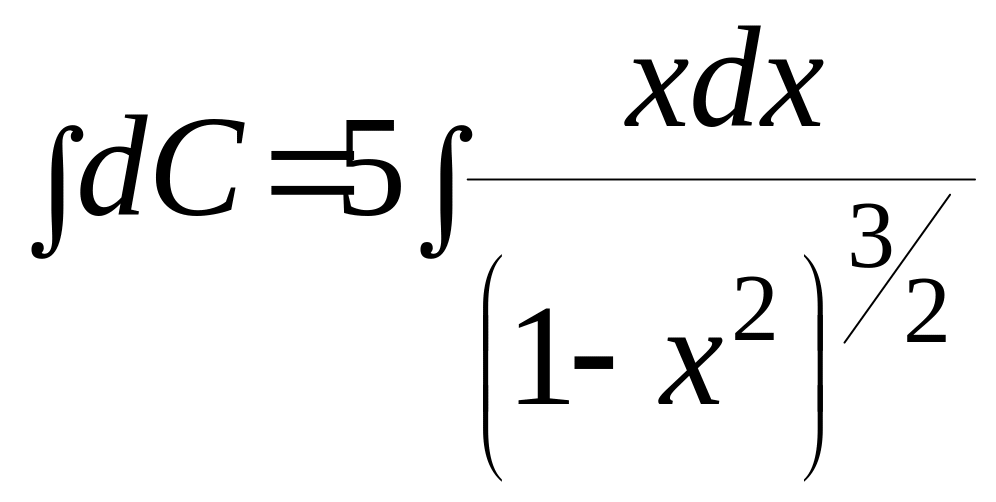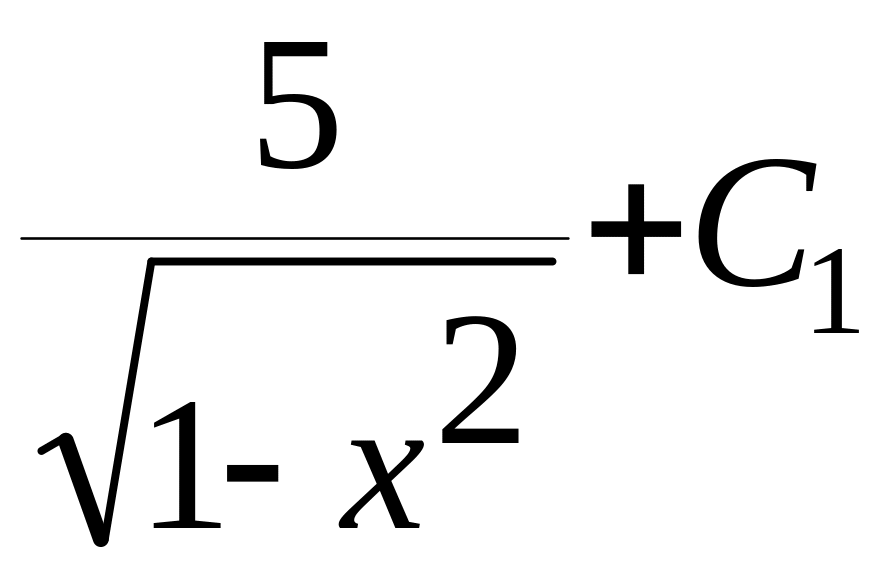= , де -довільна стала .

Остаточно маємо такий загальний розв’язок д.р. (2.3.5) :

Відповідь: .

Спосіб підстановки Бернуллі

Виражаємо шукану функцію добутком двох функцій від х : ,

, отже д.р. (2.3.1) приймає вигляд :

,

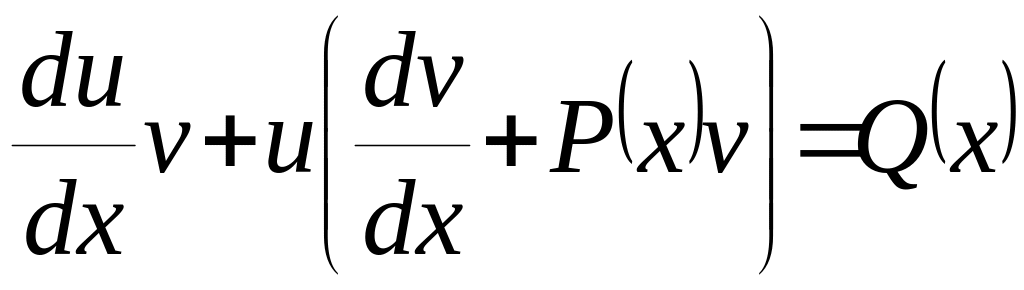, . (2.3.7)

Виберемо функцію таку , щоб ,

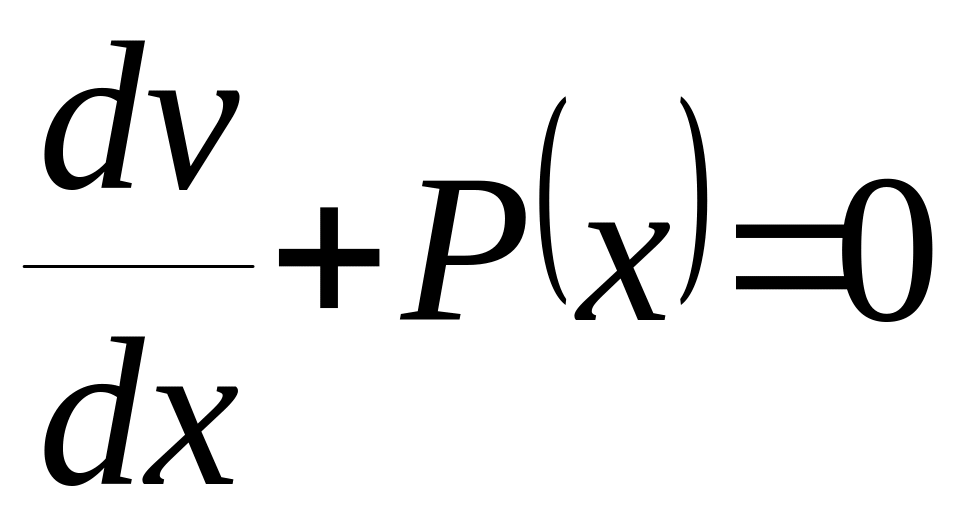= , +С .

Поза як нам треба вибрати лише одну якусь з функцій , яка перетворює дужки в нуль, то можемо взяти найпростішу з них : .Підставимо це в (2.3.7)

та отримаємо д.р. з відокремленими змінними відносно функції , розв’язавши яке та ,помноживши знайдений розв’язок на отримаємо загальний розв’язок д.р. (2.3.1).

Продемонструємо цей спосіб на прикладі (2.3.5).

,

, ,

, ,

, ,

, ( ) ,

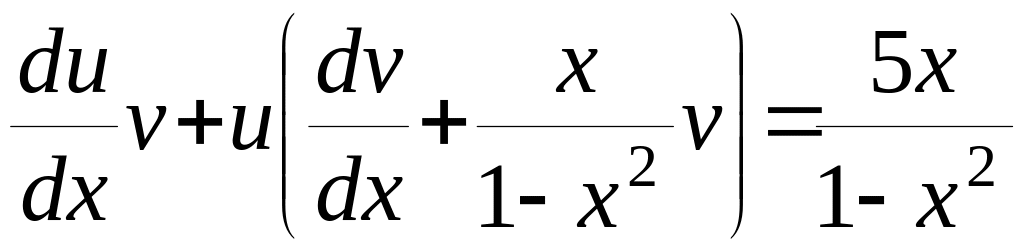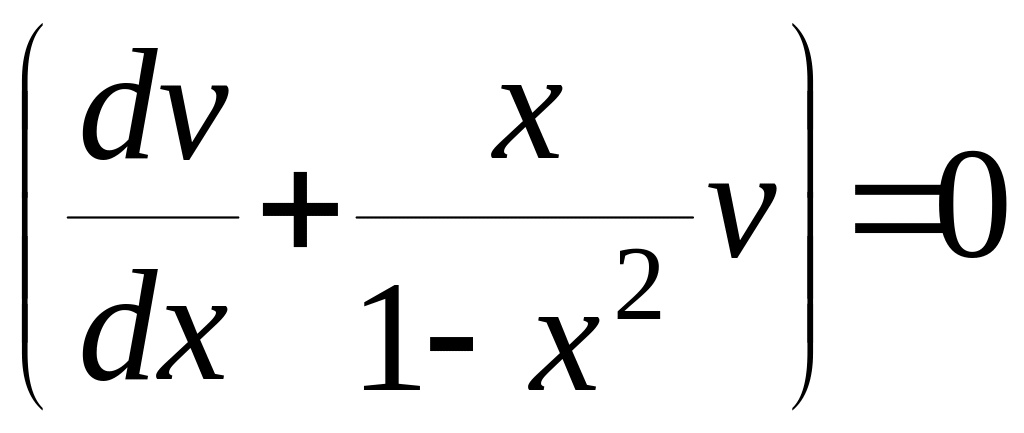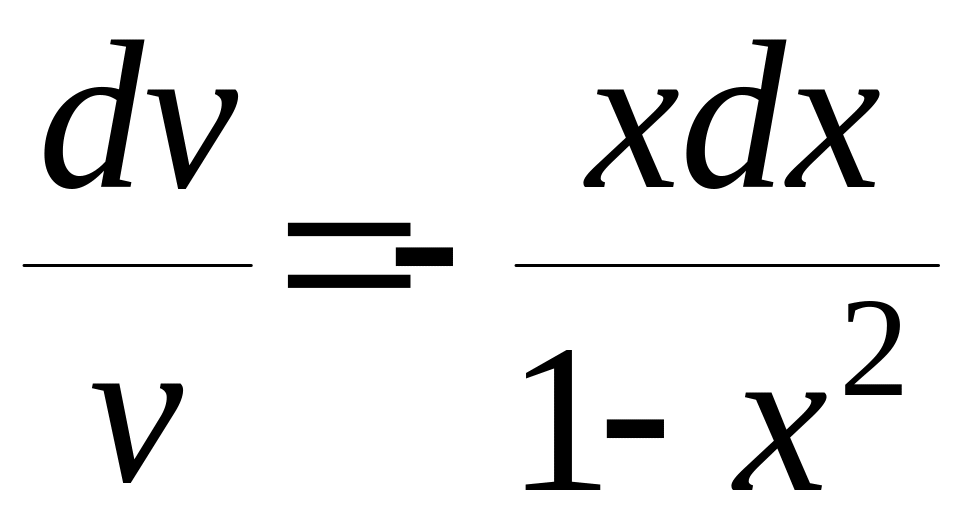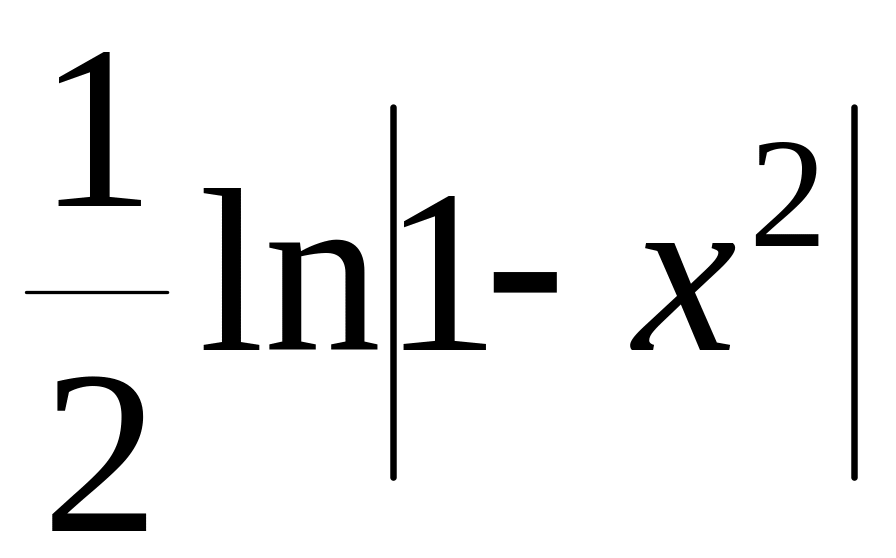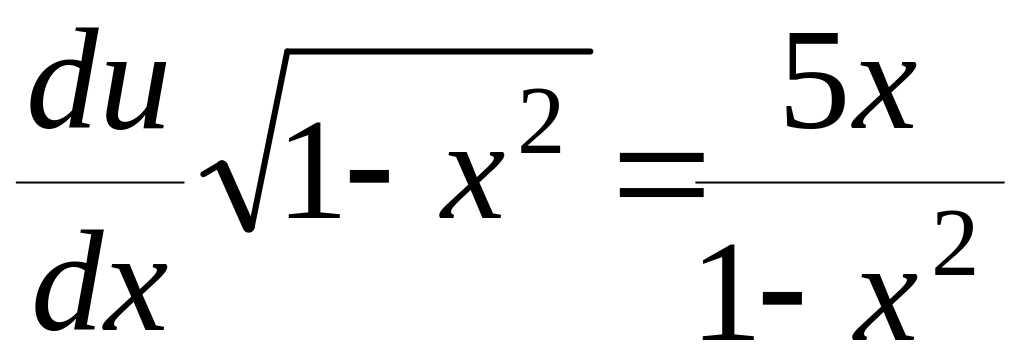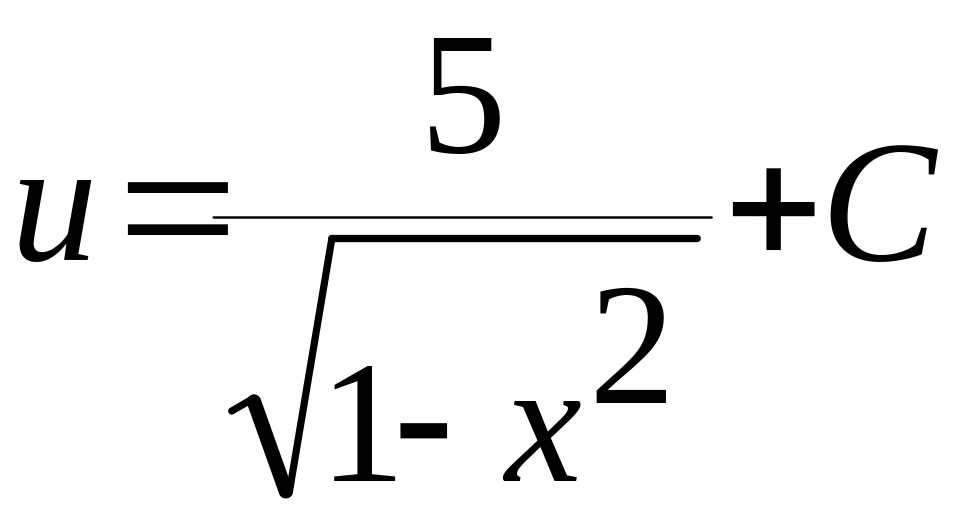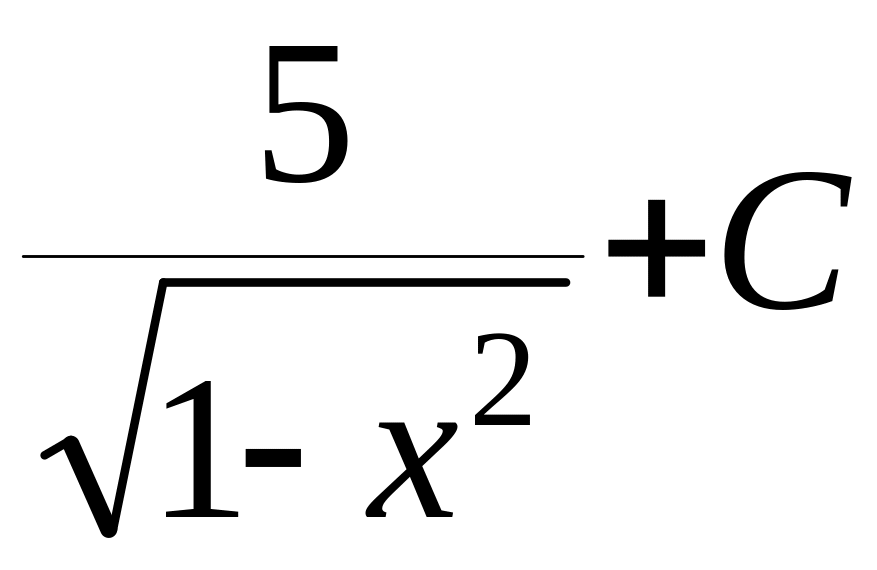Відповідь: ,

що співпадає з результатом , отриманим при використанні методу варіації сталої.

Деякі д.р. є нелінійними по у , але лінійними по х. Наприклад :

.

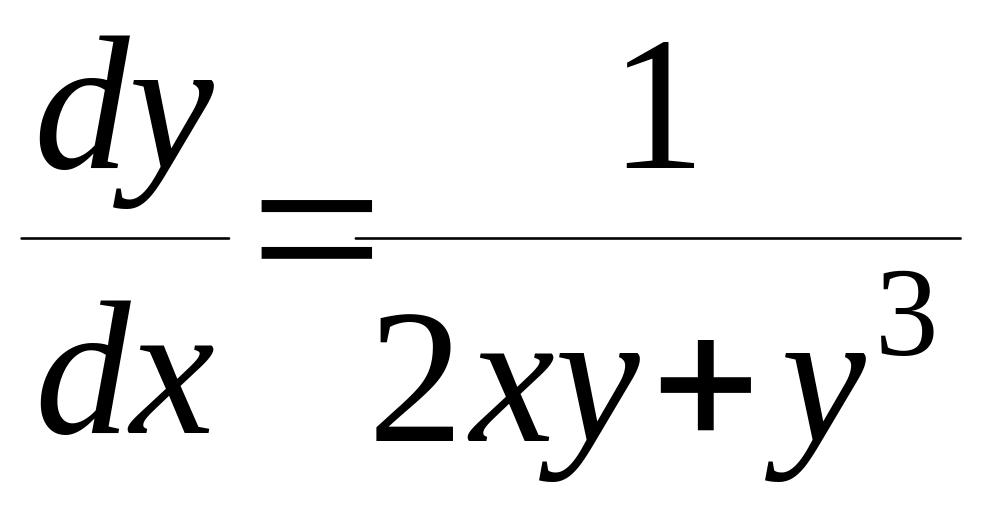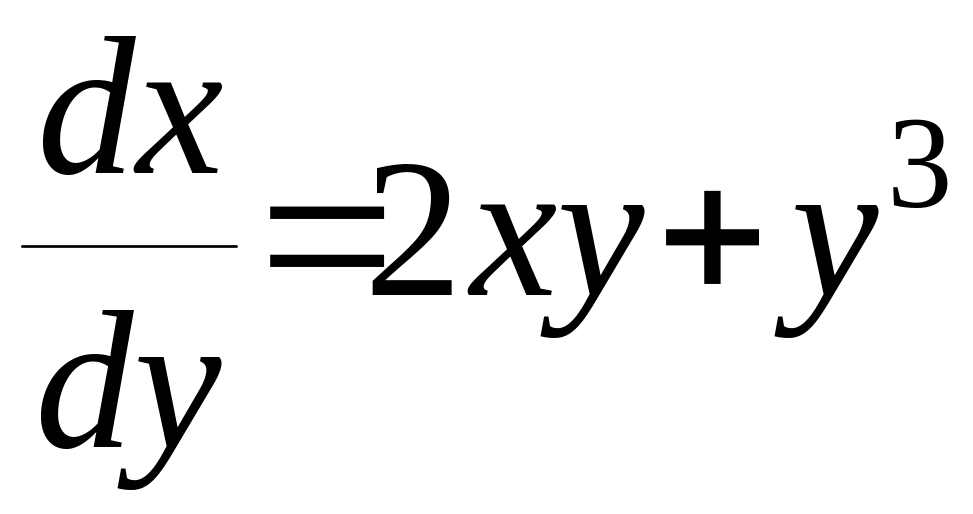є лінійним неоднорідним д.р. для невідомої функції , у розглядаємо як незалежну змінну.Використаємо підстановку Бернуллі.

, ,

, ,

, , , ,

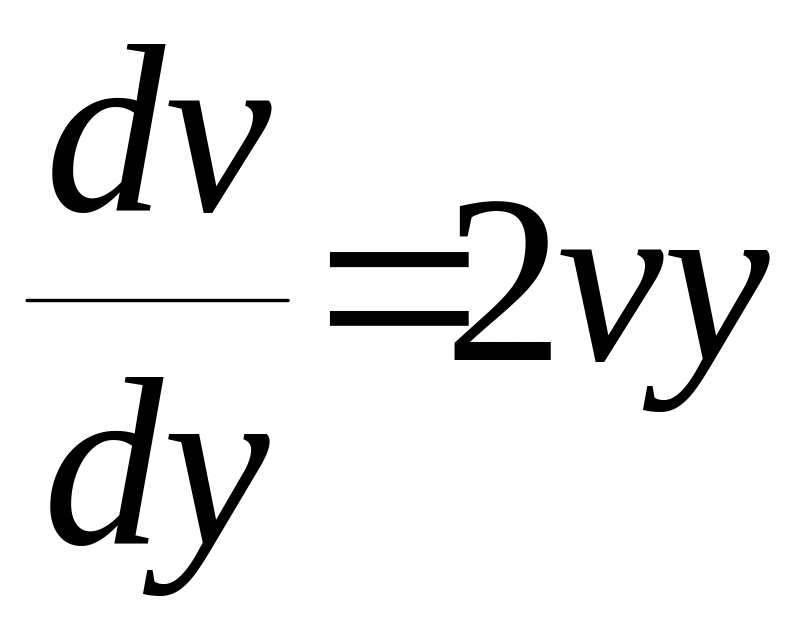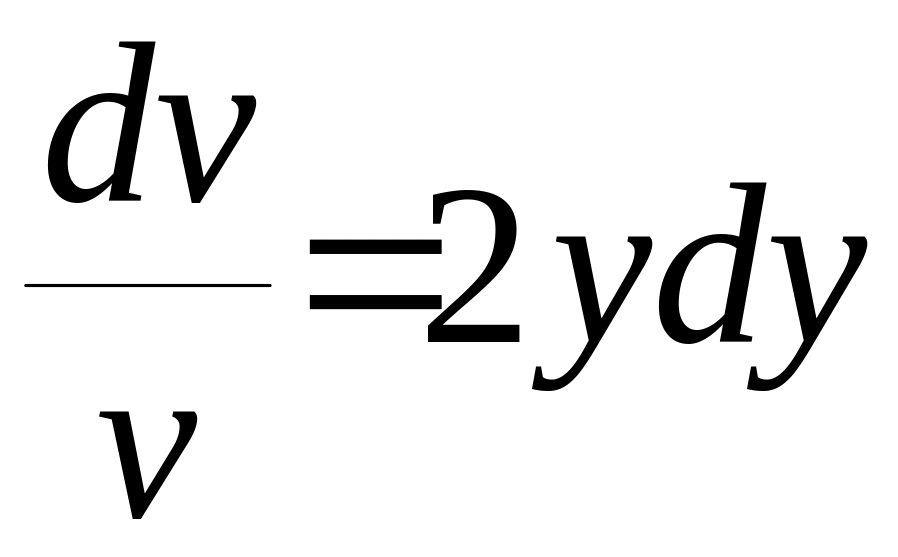, , u= .

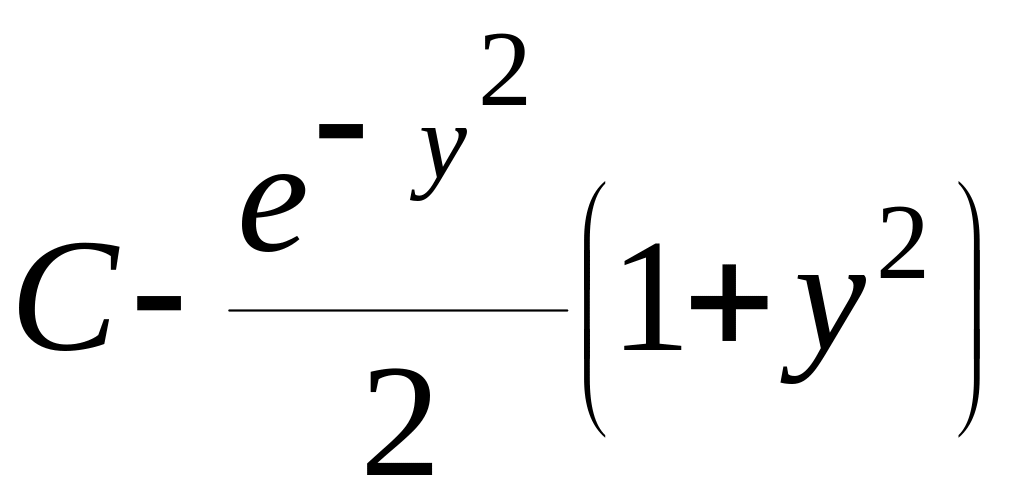Відповідь: .
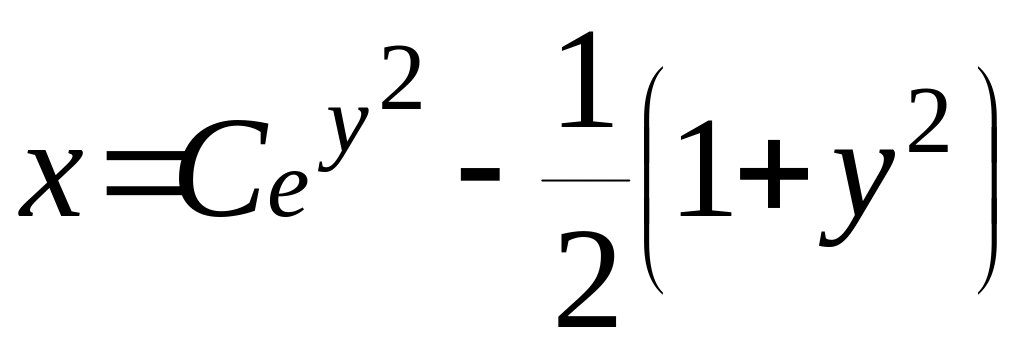