
- •Класифікація засобів комп’ютерної математики
- •3. Призначення та основні функції Scilab.
- •5. Середовище Scilab
- •6. Текстові коментарі та елементарні математичні вирази.
- •7. Змінні в Scilab
- •11. Спеціальні матричні функції
- •12. Функція plot і plot2d
- •13. Оформлення графіків.
- •14. 2. Побудова тривимірних графіків в Scilab
- •18. Файл функції та файл сценарію.
18. Файл функції та файл сценарію.
Файл-сценарій це список команд Scilab, збережений на диску. Для підготовки, редагування і відладки файлів-сценаріїв служить спеціальний редактор SciPad, який можна викликати, виконавши команду головного меню Editor.
В результаті роботи цієї команди буде створений новий файл-сценарій.
Вікно редактора файлів-сценаріїв виглядає стандартно, тобто має заголовок, меню, панелі інструментів, рядок стану. Введення тексту у вікно редактора файлу-сценарію здійснюється за правилами, прийнятим для команд Scilab. Крапка з комою <;> ставиться після тих команд, які не вимагають виведення значень.
Для збереження введеної інформації необхідно виконати команду File - Save з меню редактора. Якщо інформація зберігається вперше, то з'явиться вікно Save file As... .
Відкриває раніше створений файл команда головного меню File - Open.
Виконати оператори файлу-сценарію можна декількома способами:
• з меню редактора SciPad викликати команду Execute - Load into Scilab;
• з головного меню Scilab викликати команду Exec і вказати ім'я файлу-сценарію.
Всі ці дії призведуть до появи в робочій області результатів обчислень команд файлу-сценарію
Всі функції, використовувані в Scilab, можна розділити на два класи:
• вбудовані;
• визначені користувачем.
У загальному вигляді звернення до функції в Scilab має вигляд:
ім'я_змінної = ім’я_функції (переменная1 [, переменная2, ...])
де ім'я_змінної - змінна, в яку будуть записані результати;
ім’я_функції - ім'я вбудованої або раніше створеної користувачем функції;
переменная1, переменная2, ... список аргументів функції.
Функція, як правило, призначена для неодноразового використання, вона має вхідні параметри і не виконується без їх попереднього задання.
Перший спосіб це застосування оператора deff, який в загальному вигляді можна записати так:
deff ('[ім'я 1, ..., ім'я N] = ім'я_функції (змінна _1, ..., змінна _M)',
'ім'я 1 = вираз 1; ...; ім'я N = вираз N')
де ім'я 1, ..., ім'я N-список вихідних параметрів, тобто змінних, яким буде привласнений кінцевий результат обчислень,
ім'я_функції -ім'я з яким ця функція буде викликатися,
змінна _1, ..., змінна_M-вхідні параметри.
Другий спосіб створення функції це застосування конструкції виду:
function [ім'я 1, ..., ім'я N] = ім'я_функції (змінна _1, ..., змінна _M)
тіло функції
endfunction
де ім'я1, ..., ім'яN –список вихідних параметрів, яким буде привласнений кінцевий результат обчислень; ім'я_функції –ім'я з яким ця функція буде викликатися, змінна _1, ..., змінна _M –вхідні параметри.
Функції, що зберігаються в окремих файлах, повинні бути попередньо завантажені в систему, за допомогою оператора exec (ім'я _файла)
19. Scilab дозволяє створювати не лише звичайні програми для автоматизації розрахунків, але і візуальні застосування, які запускатимуться в середовищі Scilab. Основним об'єктом в середовищі Scilab є графічне вікно.
Робота з графічним вікном
Для створення порожнього графічного вікна служить функція figure.
F=figure();
В результаті виконання цієї команди буде створено графічне вікно з ім'ям objfigure1. За умовчанням перше вікно отримує ім'я objfigure1, друге _objfigure2 і т. д. Покажчик на графічне вікно1 записується в змінну F. Розмір і положення вікна на екрані комп'ютера можна задавати з допомогою параметра
'position[x y dx dy],
де x, y _положення верхнього лівого кута вікна (по горизонталі і вертикалі відповідно) відносно верхнього лівого кута екрану;
dx _розмір вікна по горизонталі (ширина вікна) в пікселях;
dy _розмір вікна по вертикалі (висота вікна) в пікселях.
Пiд покажчиком ми розумітимемо змінну, в якій зберігається адреса вікна або іншого об'єкту.
Параметри вікна можна задавати одним з двох способів:
1. Безпосередньо при створенні графічного вікна задаються його параметри.
В цьому випадку звернення до функції figure має вигляд
F=figure('Властивість 1 ', 'Значення 1 ', 'Властивість 2
'Значення 2 ', .., 'Свойствоn ', 'Значенняn')
Наприклад, за допомогою команди
F=figure('position ', [10 100 300 200]); буде створено вікно.
2. Після створення графічного вікна за допомогою функції
set(f','Свойство','Значення)
встановлюється значення параметрів; тут f_покажчик на графічне
вікно, 'Властивість'_ім'я параметра, 'Значення'_його значення.
Наступні два рядки задають місцерозташування і розмір вікна.
f=figure();
set(f', position[20,40,600,450])
На лістингу 10.1 приведений при-
заходів створення вікна з ім'ям FIRST WINDOWS.
Лістинг 10.1. Створення вікна з ім'ям FIRST WINDOW
f=figure();
set(f', position[20,40,600,450]);
set(f', figure_name ',' FIRST WINDOW');
Це ж вікно можна отримати за допомогою одного рядка
f=figure('position[20,40,600,450]figure_name ',' FIRST WINDOW');
Графічне вікно можна закрити за допомогою функції
close(f)
тут f_покажчик на вікно.
Видаляється вікно за допомогою функції
delete(f)
де f_покажчик на вікно.
Динамічне створення інтерфейсних елементів.
Опис основних функцій
У Scilab використовується динамічний спосіб створення інтерфейсних компонентів. Він полягає в тому, що на стадії виконання програми можуть створюватися (і віддалятися) ті або інші елементи управління (кнопки, мітки
прапорці і т. д.) і їх властивостям привласнюються відповідні значення.
Для створення будь-якого інтерфейсного компонента із заданими властивостями
використовується функція uicontrol, що повертає покажчик на формований
компонент:
C=uicontrol(F, 'Style ', 'тип_компонента', 'Властивість_1
Значення_1, 'Властивість_2 ', Значення_2,..
'Властивість_k ', Значення_k);
Тут C _покажчик на створюваний компонент;
F _покажчик на об'єкт, усередині якого створюватиметься компонент (частіше
всього цим компонентом буде вікно); перший аргумент функції uicontrol
не є обов'язковим, і якщо він відсутній, то батьком (владель-
цем) створюваного компонента являється поточний графічний об'єкт_те-
кущее графічне вікно;
'Style' _службовий рядок Style, вказує на стиль створюваного компонен-
та (символьне ім'я);
'тип_компонента' _визначає, до якого класу належить створюваний
компонент, це може бути PushButton, Radiobutton, Еdit, StaticText
Slider, Panel, Button Group, Listbox або інші компоненти, це свой-
ство вказуватиметься для кожного з компонентів;
'Властивість_k ', Значення_k _визначають властивості і значення окремих компо-
нентов, вони будуть описані нижче конкретно для кожного компонента.
У існуючого інтерфейсного об'єкту можна змінити ті або інші свой-
ства за допомогою функції set :
set(C,'Свойство_1 ', Значення_1, 'Властивість_2 ', Значення_2, ..
'Властивість_k ', Значення_k)
Тут C _покажчик на динамічний компонент, параметри якого будуть ме-
няться. C може бути і вектором динамічних елементів, в цьому випадку
функція set задаватиме значення властивостей для усіх об'єктів C(i);
'Властивість_k ', Значення_k _змінювані параметри і їх значення.
Набути значення параметра компонентів можна за допомогою функції get
наступної структури:
get(C','Свойство)
Тут C _покажчик на динамічний інтерфейсний компонент, значення пара-
метра якого необхідно дізнатися;
'Властивість' _ім'я параметра, значення якого треба упізнати.
Функція повертає значення параметра.
20. Робота з поліномами
Операції над поліномами. Будь-яке рівняння P(x)=0, де P(x) – це багаточлен, відмінний від нульового, називається алгебраїчним рівнянням або поліномом. Усяке алгебраїчне рівняння відносно х можна записати у вигляді а0хn+a1xn-1+…+an-1x+an=0.
Розв’язання алгебраїчного рівняння в scilab складається із двох етапів. Необхідно задати поліном P(x) за допомогою функції poly, а потім знайти його корінь, застосувавши функцію roots.
Отже визначення поліномів в scilab здійснює функція
Poly(a,’x’,’fl’)
де а – це число або матриця чисел, х – символьна змінна, fl – необов’язковий символьний змінний, визначальний спосіб задання полінома. символьна змінна fl може приймати тільки 2 значення – roots або coeff (відповідно r або c). Якщо fl=с, то буде сформований поліном з коефіцієнтами, що зберігаються в параметрі а. якщо ж fl= r, то значення параметра а сприймаються функцією як корені, для яких необхідно розрахувати коефіцієнти відповідного полінома. За замовчуванням fl= r.
Функція roots(р) призначена для розв’язування алгебраїчного рівняння. Тут р – це поліном, створений функцією Poly і має вигляд лівої частини рівняння P(x)=0.
21. Будь-яке рівняння Р(х) = 0, де Р(х) це багаточлен, відмінний від нульового, називається алгебраїчним (лінійним)рівнянням або поліномом. Усяке алгебраїчне рівняння відносно х можна записати у вигляді а0хn+а1хn-1+...+аn-1х+аn = 0, де аі— коефіцієнти алгебраїчного полінома n-го степеня, а0 = 0.
Розв'язання алгебраїчного рівняння в Sсіlаb складається із двох етапів. Необхідно задати поліном Р(х) за допомогою функції роlу, а потім знайти його корінь, застосувавши функцію roots.
Отже, визначення поліномів в Sсіlаb здійснює функція роlу (а, 'х', ‘fl’), де а — це число або матриця чисел, х — символьна змінна, fl — необов'язковий символьний змінний, визначальний спосіб задання полінома. Символьна змінна fl може приймати тільки два значення — «roots» або «соеff» (відповідно «r» або «с»). Якщо fl=с, то буде сформований поліном з коефіцієнтами, що зберігаються в параметрі а. Якщо fl=r, то значення параметра а сприймаються функцією як корені, для яких необхідно розрахуватикоефіцієнти відповідного полінома. За замовчуванням fl=r.
Функція roots(р) призначена для розв'язання алгебраїчного рівняння. Тут р — це поліном, створений функцією роlу і має вигляд лівої частини рівняння Р(х)=0. Для розв'язання трансцендентних рівнянь в Scilab застосовують функцію fslove(x0, f), де х0 — початкове наближення, f— функція, що описує ліву частину рівняння f(х) = 0.
Послідовно викликаючи функцію fslove з різними початковими наближеннями, можна одержати всі розв'язки заданого рівняння
Крім того, початкові наближення можна задати у вигляді вектора, і тоді функцію можна викликати один раз.
Якщо задані n рівнянь із n невідомими потрібно знайти послідовність із n чисел, які одночасно задовольняють кожному з n рівнянь, то говорять про систему рівнянь. Для рішення систем рівнянь в Scilab також застосовують функцію fslove(x0, f).
22. Розвязування алгебраїчного рівняння в Scilab складається з двох етапів. потрібно задати поліном P (x) за допомогою функції poly, а потім знайти його корінь, застосувавши функцію roots. Отже, визначення поліномів в Scilab здійснює функція poly (a, "x [" fl "]), де a це число або матриця чисел, x символьна змінна, fl необов'язкова символьна змінна, яка визначає спосіб задання полінома. Символьна змінна fl може приймати тільки два значення roots або coeff (відповідно r або c ). Якщо fl = c, то буде сформований поліном з коефіцієнтами, що зберігаються в параметрі a. Якщо ж fl = r, то значення параметра a сприймаються функцією як корінь, для яких необхідно розрахувати коефіцієнти відповідного полінома. По замовчування fl = r.
Функція roots (p) призначена для розвязку алгебраїчного рівняння. Тут p Це поліном, створений функцією poly і представляє собою ліву частину рівняння P (x) = 0.
Чисельний розвязок нелінійного рівняння проводять у два етапи. На початку відокремлюють корені рівняння, тобто знаходять досить тісні проміжки, в яких міститься тільки один корінь. Ці проміжки називають інтервалами ізоляції кореня, визначити їх можна, зобразивши графік функції f (x). На другому етапі проводять уточнення відокремлених коренів, або, інакше кажучи, знаходять корені із заданою точністю. Для вирішення трансцендентних рівнянь у Scilab застосовують функцію fsolve (x0, f) де x0 початкове наближення, f функція, що описує ліву частину рівняння y (x) = 0.
Якщо задані m рівнянь з n невідомими і потрібно знайти послідовність з n чисел, які одночасно задовольняють кожному з m рівняння, то говорять про систему рівнянь. Для вирішення системи рівнянь в Scilab також застосовують функцію fsolve (x0, f).
23. Метод найменших квадратів дозволяє за експериментальними даними дібрати таку аналітичну функцію, яка проходить настільки близько до експериментальних точок, наскільки це можливо.
Нехай в результаті експерименту були отримані деякі дані, відображені у вигляді таблиці. Вимагається побудувати аналітичну залежність, таку, що найточніше описує результати експерименту.

Ідея методу найменших квадратів полягає в тому, що функцію Y = f(x, a0, a1, . . ., ak) необхідно підібрати так, щоб сума квадратів відхилень виміряних значень yi від розрахункових Yi була найменшою :
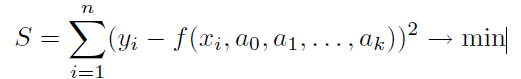
Завдання зводиться до визначення коефіцієнтів ai з умови таблиці. Для реалізації цього завдання в Scilab передбачена функція
[S]=datafit(F, z, с)
де F-функція, параметри якої необхідно підібрати; z-матриця
вихідних даних; c-вектор початкових наближень; a-вектор коефіцієнтів;
S-сума квадратів відхилень виміряних значень від розрахункових.
24. Інтерполяція функцій Найпростіша задача інтерполяції полягає в наступному. На відрізку [A; b] задані точки x0, x1, x2,. . . , Xn (всього n +1 точка), які називають вузлами інтерполяції, і значення деякої функції f (x) в цих точках: f (x0) = y0, f (x1) = y1, f (x2) = y2,. . . , F (xn) = yn. (11.4) Потрібно побудувати интерполирующую функцію F (x), що належить з- вестное класу і приймаючу у вузлах інтерполяції ті ж значення, що і f (x): F (x0) = y0, F (x1) = y1, F (x2) = y2,. . . , F (xn) = yn. (11.5) Для вирішення такого завдання досить часто використовують сплайн-інтерполяцію. Один з найбільш розповсюдженим страненно варіантів інтерполяції? інтерполяція кубічними сплайнами. Крім того, існують квадратичні і лінійні сплайни. У Scilab для побудови лінійної інтерполяції служить функція y = interpln (z, x) z-матриця вихідних драних; x- вектор абсцис; y-вектор значень лінійно сплайна в точка x. Побудова кубічного сплайна в Scilab складається з двох етапів: 1- внача- ле обчислюються коефіцієнти сплайна за допомогою функції
d = splin (x, y), x-суворо зростаючий вектор, що складається мінімум з двох компонент; y-вектор того ж формата, що і x; d-результат роботи функції, коефіцієнти кубічного сплайна. 2-а потім розраховується значення інтерполяційного полінома в точці
y = interp (t, x, y, d). y і d мають ті ж значення, t- це вектор абсцис, а y- вектор ординат, які є значеннями кубічного сплайна в точках x.
25. Знаходження мінімуму функцій. Для знаходження значення мінімуму функції в Scilab служить функція [F, xopt] = optim (costf, x0), яка призначена для пошуку мінімуму будь-якої функції, x0 вектор-стовпець початкових наближень довжиною n, функція costf визначає функцію, мінімум якої шукається. Функція повертає мінімум функції (f) і точку, в якій функція досягає цього значення (xopt). Головною особливістю функції optim є структура функції costf, яка повинна бути наступною: function [f, g, ind] = costf (x, ind) / / Функція costf повинна повертати функцію f, її градієнт g. / /f - функція від вектора невідомих х, мінімум якої шукається f = gg (x); / / g - градієнт функції f (вектор часткової похідної f по x), g = numdiff (gg, x); endfunction Для функції однієї змінної в якості f повертається функція, мінімум якої шукається, в якості функції g - її похідна. Якщо повертається сформоване функцією costf значення ind дорівнює 2, 3 або 4, то функція costf забезпечує пошук мінімуму, тобто в якості результату функції optim повертається f і xopt. Якщо ind = 1, то в функциии optim нічого не рахує, умова ind <0 означає, що мінімум f (x) не може бути оцінений, а ind = 0 перериває оптимізацію. При використанні функції optim необхідно сформувати функцію costf, яка повинна повертати мінімізуючу функцію f і її градієнт (похідну). Приклад: Пошук мінімуму функції однієї змінної f(x) = x4 + 3x3 − 13x2 − 6x + 26 / / Функція fi, в якій буде формуватися функція f і її / / Похідна g. function [f, g, ind] = fi (x, ind) / / Функція f, мінімум якої шукається. f = x ^ 4 +3 * x ^ 3-13 * x ^ 2-6 * x +26 / / Функція g - похідна від функції f. g = 4 * x ^ 3 +9 * x ^ 2-26 * x-6 endfunction / / Початкове наближення точки мінімуму. y0 = -2; / / Для пошуку точки мінімуму (xmin) і значення функції (fmin) в / / ній - виклик функції optim. [Fmin, xmin] = optim (fi, y0); Нижче представлений результат пошуку мінімуму функції однієї змінної: -> Fmin fmin = - 95.089413 -> Xmin xmin = 3.8407084 Аналогічно можна знайти мінімум будь-якої іншої функції однієї змінної, головним завданням є проблема правильного вибору точки початкового наближення. Але це проблема не пакета Scilab, а математична проблема.
26. В Scilab чисельне інтегрування по методу трапецій реалізовано за допомогою функції inttrap(x,y)
x- вектор значень проміжка [a,b]
y-вектор значень функції в точках х
Напр, x=[0:0.5:2];
y=sqrt(x./(a-x));
I=inttrap(x,y)
Обчислювальний алгоритм квадратурних формул реалізовано функцією
integrate(‘func’,’x’,a,b), де
func – підінтегральна функція задана в символьному вигляді
х – аргумент заданй в символьному вигляді,
а і b – межі інтегрування
Напр, deff('y=f(x)','y=sqrt(x./(a-x))');
I2=integrate('f','x',0, 2)
Найбільш універсальною функцією для пошуку інеграла в скайлаб є
intg(a,b,func), де
а і b – межі інтегрування
func – підінтегральна функція
Напр, deff('y=f(x)','y=sqrt(x./(a-x))');
I1=intg(0,2,f)
Для чисельного диференціювання, тобто пошуку похідної в конкретній точці викор функція:
numdiff(func,x)
Напр, deff('y=f(x)','y=(1-x.^2).^2')
p=numdiff(f,2);
27. Для розв’язування диференціальних рівнянь і систем в Scilab передбачена функція [y]=ode([type],y0,t0,t)
Де у0 – вектор почткових умов;
t0 – початкова точка інтервалу інтегрування;
t – координати вузлів сітки, у яких відбувається пошук розвязку;
f – зовнішня функція, що визначає праву частину рівняння або системи рівнянь;
у – вектор розвязку.
28. Для вирішення задач лінійного програмування в Scilab призначена функція linpro наступної структури:
[x, kl, f] = linpro (с, A, b[, ci, cs] [, k] [, x0])
Тут c — масив (вектор-стовпець) коефіцієнтів при невідомих функції цілі, довжина вектора n співпадає з кількістю невідомих x.
A — матриця при невідомих з лівої частини системи обмежень, кількість рядків матриці дорівнює кількості обмежень m, а кількість стовпців
збігається з кількістю невідомих n.
b - масив (вектор-стовпець), містить вільні члени системи обмежень, довжина вектора m.
ci - масив (вектор-стовпець) розмірності n містить нижню межу змінних (cij ≤ xj); якщо така відсутня, вказують [].
cs - масив (вектор-стовпець) довжиною n, містить верхню межу змінних (csj>xj); якщо така відсутня, вказують [].
k - цілочисельна змінна, використовується, якщо в систему обмежень крім нерівностей входять і рівності, в матриці вони будуть знаходитися в k перших рядках, l рядків що залишилися займуть нерівності, тобто m = k + l.
x0 - вектор-стовпець початкових наближень довжиною n.
Функція linpro повертає масив невідомих x, мінімальне значення функції f і масив множників Лагранжа kl.
