Лекция 4. Второй закон термодинамики (4) план

1. ЭНТРОПИЯ

2. ОБЩАЯ ФОРМУЛИРОВКА ВТОРОГО ЗАКОНА

3. ПРЯМОЙ ЦИКЛ КАРНО

4. ОБОБЩЕННЫЙ (РЕГЕНЕРАТИВНЫЙ) ЦИКЛ КАРНО

5. ОБРАТНЫЙ ЦИКЛ КАРНО

6. СТАТИСТИЧЕСКОЕ ТОЛКОВАНИЕ ВТОРОГО

НАЧАЛА ТЕРМОДИНАМИКИ

7. ЭКСЕРГИЯ

1. Энтропия

Как уже указывалось, величина не является полным дифференциалом. Действительно, для того чтобы проинтегрировать правую часть этого выражения, нужно знать зависимость р от , т.е. процесс, который совершает газ.

В математике доказывается. Что дифференциальный двучлен всегда можно превратить в полный дифференциал путем умножения (или деления) на интегрирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты является абсолютная температура Т.

Покажем это на примере изменения параметров идеального газа в равновесных процессах:

(1)

Выражение при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Она называется энтропией, обозначается для 1 кг газа через и измеряется в Дж/(кгК). Для произвольного количества газа энтропия, обозначаемая через S, равна S=Ms и измеряется в Дж/К

Таким образом, аналитически энтро­пия определяется следующим образом:

(2)

Формула (2) справедлива как для идеальных газов, так и для реальных тел.

Подобно любой другой функции со­стояния энтропия может быть представ­лена в виде функции любых двух пара­метров состояния:

. .

Значение энтропии для заданного со­стояния определяется интегрированием уравнения (2):

где - константа интегрирования.

При температурах, близких к абсо­лютному нулю, все известные вещества находятся в конденсированном состоя­нии. В. Нернст (1906 г.) эксперименталь­но установил, а М. Планк (1912 г.) окон­чательно сформулировал следующий принцип: при температуре, стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном со­стоянии с упорядоченной кристалличе­ской структурой, стремится к нулю, т. е. = 0 при Т = 0 ^оК. Этот закон на­зывают третьим законом термодинамики или тепловой тео­ремой Нернста. Он позволяет рассчитать абсолютное значение энтропии в отли­чие от внутренней энергии и энтальпии, которые всегда отсчитываются от про­извольного уровня.

Однако в технической термодинамике обычно используется не абсолютное зна­чение энтропии, а ее изменение в каком-либо процессе:

(3)

поэтому энтропию тоже часто отсчитыва­ют от произвольно выбранного уровня.

Получим формулы, позволяющие вы­числить изменение энтропии идеального газа. Для этого проинтегрируем уравне­ние (3.1), положив для простоты = const:

(4)

Из уравнения Клапейрона, записан­ного для состояний 1 и 2, следует:

После подстановки отношений и в выражение (4) получим сле­дующие формулы для изменения энтро­пии идеального газа:

(5)

(6)

Поскольку энтропия есть функция со­стояния рабочего тела, уравнениями (4)…(6) можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями 1 и 2 и, в частности, от того, равновесный этот переход или нет.

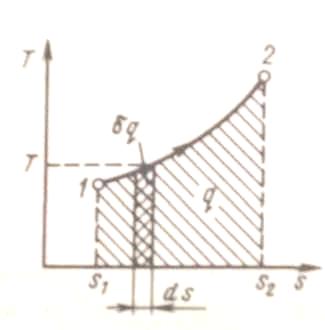
Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов Т, s - диаграмму, на которой (как и на р, -диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией (рис. 1).

Рис. 1. Графическое изображение теплоты в Т, s-координатах