3. Параметры состояния рабочего тела.

Основными параметрами состояния рабочего тела (газа или пара) являются: давление (р), температура (t, Т) и удельный объем (v). Предварительно отметим, что плотностью вещества ρ называют массу (кг) единицы объема (м³) его. Так, если масса объема V какого-либо газа равна G, то

, кг/м³ (1)

Давление р означает силу, приходящуюся на единицу площади, и определяется формулой

, Па (2)

где N - сила, нормальная к поверхности и равномерно распреде­ленная по площади, Н;

F – площадь, м².

Давление измеряется в кГ/см², кГ/м², Н/м², а иногда в метрах или миллиметрах столба жидкости (воды, ртути, спирта).

В термодинамике давление рабочего тела иногда измеряют в физических или технических атмосферах.

Абсолютное или истинное давление определяется суммой избыточного и барометрического давлений (рис.1):

(3а)

Если в сосуде давление ниже атмосферного, то имеет место разряжение. Разность между барометрическим и абсолютным давлением называется вакуумом, или разряжением, т.е.

(3б)

Рисунок 1- К определению абсолютного давления

Размер- ность Наимено-вание	кгс/см2	кгс/м2	мм. рт. ст.	м. рт. ст.	мм. вод. ст.	м. вод. ст.
1 физ. атм-ра	1,033	1,03·10	760	0,76	1,03·10	10,3
1 техн. атм-ра	1,0	1·10	735,6	0,735	1·10	10
1 бар	1,02	1,02·10	750	0,75	1,02·10	10,2

Давление окружающей среды, например, атмосферного воздуха, фиксируется, как известно, прибором барометром и называется барометрическим.

Давление выше барометрического измеряется манометром и называется избыточным, или манометрическим.

Давление ниже барометрического (вакуум, или разрежение) измеряется вакуумметрами или тягомерами.

Если показание ртутного барометра при температуре t°С равно , то приведение этого показания к нулю можно производить по формуле

(4)

С увеличением высоты Н в пределах тропосферы (до 11 000 м) барометрическое давление снижается по закону

, (5)

где - барометрическое давление на высоте Н при 0°С;

Н - высота над уровнем моря, м.

Замеряя давление газа в емкости по манометру, узнаем, насколько истинное давление в емкости пре­вышает давление окружающей среды. Поэтому, чтобы отыскать истинное или абсолютное давление газа в емкости, следует всегда к показанию манометра прибавить давление окружающей среды (т. е. прибавить величину барометрического давления р_б)

Температура - мера нагретости тела, характеризую­щая его тепловое состояние. Однако хорошо всем известное ка­чественно воспринимаемое ощущение температуры количественно (физически) определяется сложно. Измерение температуры осно­вано на следующем факте если два тела, взятых порознь, находятся в термическом равновесии при соприкосновении с третьим телом, то все три тела имеют одну и ту же температуру. В основу прибора, измеряющего температуру (термометра), положено явление расширения тел при нагревании. С тем же успехом можно воспользоваться другими свойствами, например э. д. с. термо­пары, электросопротивлением материалов, радиацией и пр. Все эти способы измерения температуры не позволяют, однако, опре­делить ее как некоторую величину, не зависящую от свойств термо­метрического вещества,

В 1721 г. голландцем Фаренгейтом был предложен термометр, в котором за 0° принята температура смеси равных частей льда и нашатыря. В этой шкале температура таяния льда равна +32°F, а температура кипения химически чистой воды равна -212°F. Этот термометр имеет распространение главным образом в странах США, Канаде и др.

Шкала Реомюра (°R) имеет следующие базисные (реперные) точки температуры: 0° - соответствует температуре таяния льда, +80° - соответствует температуре кипения воды при нормаль­ном атмосферном давлении. Реперными точками стоградусной шкалы Цельсия(°С) соответственно являются: 0°С - температура таяния льда и + 100°С - температура кипения воды при нормальном атмосферном давлении. На рис. 3 приведены указанные шка­лы. Связь между ними устанавливается следующими формулами:

; (6)

; (7)

; (8)

Основной единицей измерения температуры является градус, цена деления которого разная в различных шкалах.

Решением XI Генеральной конференции по мерам и весам (1960 г.) и ГОСТ 8550 - 61 предусматривается применение двух температурных шкал: термодинамической и международной - практической. Единицей измерения температуры по термодинами­ческой шкале является Кельвин (К). Кельвин впервые ввел абсолютную температуру как величину, не зависящую от свойств вещества. В основу термодинамической шкалы темпера­тур положена одна экспериментальная постоянная величина - тройная точка воды, температура которой принята равной 273,15 К и которая является точкой температурного равновесия для всех трех агрегатных состояний воды (лед, жидкость, пар). Значение температуры тройной точки воды в настоящее время определя­ется с очень высокой точностью в 0,0001°. Таким образом, градус Кельвина составляет 1/273,15 части интервала от абсолютного нуля температуры до температуры тройной точки.

, К

(9)

, ^оС.

Молекулярно-кинетичеекая теория га­зов позволяет оценивать температуру как меру кинетической энергии движения молекул тела, или, иначе говоря, как функцию скорости движения их.

В Украине принята стоградусная шкала температур, по существу совпадающая со шкалой Цельсия.

Удельным объемом вещества называют объём единицы массы (кг) его т.е.

м³/кг (10)

Нетрудно заметить, что

. (11)

Нормальные физические условия: давление равно 1 атм (р₀=760 мм рт. ст., или 101 325 Н/м²), а температура t₀ = 0 °С.

Нормальные технические условия соответствуют давлению в 1 aт. (р₀ = 735,6 мм рт. ст., или 980 665 Н/м²) и t₀ = 15°С.

ЛЕКЦИЯ 2. УРАВНЕНИЕ СОСТОЯНИЯ РАБОЧЕГО ТЕЛА И СМЕСИ ГАЗОВ

План

1. Вывод характеристического уравнения.

2. Законы идеальных газов.

3. Уравнение состояние для смеси идеальных газов.

Литература:

1. Теплотехника / Баскаков А. П., Берг В. В., Вит О. К. и др. - М.: Энергоиздат, 1991.- 224 с.

2. Теплотехника / Хазен М. М., Матвеев Г Д., Грицевский М. Е. и др.- М.: Высш. школа,1981.- 480 с.

3. Швец И.Т., Толубинский В.И., Алабовский А.Е. и др. Теплотехника - К.: "Вища школа", Головное изд - во, 1976.- 517 с.

4. Нащокин В.В. Техническая термодинамика и теплопередача. Учебн. Пособие для вузов.- 3-е изд.- М.: Высшая школа, 1980.- 469 с.

5. Кафаров В.В. Основы массопередачи. Учеб. пособие для вузов.- М.: Высшая школа, 1972.- 494 с.

1. Вывод характеристического уравнения

Рассмотренные нами газовые законы, как известно, справедли­вы при определенных условиях, а именно: закон Гей - Люссака верен при соблюдении условия р = const, справедливость за­кона Шарля ограничивается условием V = const, а закон Бойля - Мариотта имеет силу при соблюдении Т = const. Такие процессы, когда остается неизменным ка­кой-либо из перечисленных параметров, встречаются в технике довольно часто. Одна­ко значительно чаще встреча­ются более важные в практи­ке процессы, течение которых имеет место при переменном значении всех параметров. В этом случае необходимо такое уравнение, которое связывало бы между собой все три пара­метра (р, и Т). Оказывается, такое уравнение есть. Оно бы­ло впервые выведено Клайпероном и обобщено Д. И. Менделеевым.

Пусть имеется 1 кг некоторого рабочего тела (газа), состояние (I) которого определяется параметрами . Требуется пере­вести это рабочее тело из данного состояния в другое (II), характе­ризующееся параметрами р_2, v₂, T₂.

Допустим, что p₂>p₁ тогда, чтобы достигнуть значения р_{2 ,} видимо, газ надо сжать. Однако сжатие газа будем производить медленно, чтобы в процессе сжатия температура газа не измени­лась (рис.1, состояние III).

Тогда, обращая внимание на состояние I-III, замечаем, что у них общая (неизменяемая) температура . Это обстоятельство позволяет использовать в процессе перехода из состояния I в состояние III закон Бойля - Мариотта, по которому

, (1)

откуда

(2)

Сравнивая состояния III и II, замечаем, что у них общим (не­изменным) является р₂, что позволяет воспользоваться законом Гей - Люссака, по которому

, (3)

откуда

(4)

Заметим, что переход из состояния III в состояние II возможен (при р₂ = const) либо при нагревании (тогда > ), либо при охлаждении (тогда < ) (см. рис. 1). Сравнивая правые части формул (2-2) и (2-4), получим:

(5)

откуда

.

Деля обе части этого уравнения на получим:

(6)

или

(7)

Полученное уравнение называется удельным уравнением со­стояния (или уравнением Клапейрона), и является справедливым для 1 кг рабочего тела (газа), поскольку значение объема, входя­щего в него, соответствует удельному объему (об этом напоминает единица, стоящая в правой части этого равенства). Это уравнение позволяет производить расчеты при переменном значении парамет­ров состояния , а связывает их между собой величина R, которая называется удельной (поскольку речь идет об 1 кг рабо­чего тела) газовой постоянной. Если оперировать не единицей, а произвольной массой G кг, то в правую часть выражения (7) следует вместо 1 поставить G, а в левую - вместо величину V = G (где V - объем произвольной массы G газа), т. е.

pV = GRT.

Если же взять количество рассматриваемого газа, равное его молекулярной массе , или, иначе говоря, одну килограмм-молекулу его, то объем этого количества газа будет соответствовать объему моля этого газа, и тогда

. (8)

Полученное выражение называется универсальным характери­стическим уравнением.

При практическом использовании уравнения pV = GRT сле­дует всегда помнить о соответствии между массой вещества и его объемом.

Физический смысл газовой постоянной вытекает из рассмотре­ния формулы (6). Внося размерности в эту формулу, получим

(или Дж/кг град)

Величины кГ и кг не сокращаются, так как их природа разная: кГ_у стоящий в числителе, - силовая функция (вообще говоря, величина переменная в зависимости от того, где именно, в какой географической точке происходит измерение); кг, стоящий в зна­менателе, - массовая функция (величина неизменная). Для примера скажем, что си­ла тяжести (вес), измеренная в разных точ­ках земли, будет в принципе разной, а мас­са вещества в этих же точках остается неизменной.

Таким образом, получается, что газовая постоянная рабочего тела физически понимается как механическая работа (кГ×м), со­вершенная 1 кг газа при нагревании его на один градус (при по­стоянном давлении). Отметим также, что поскольку разность тем­ператур по шкале Кельвина и стоградусной одна и та же, то безразлично, к какой температуре относить эту работу газа. Иначе говоря, величина R характеризует работу газа и в значительной мере облегчает оценку и исследование процессов преобразования теплоты в работу.

Если использовать формулу (6) для нормальных условий, то получим

(10)

Из уравнения (10) вытекает, что для двух газов можно на­писать

(11)

Пользуясь уравнением (8) для нормальных условий, будем иметь

(12)

откуда

(13)

Полученная константа называется универсальной газовой по­стоянной.

Для двух газов можно написать

откуда

(14)

Так, например:

для кислорода = = 260 Дж/(кг К);

для азота = =295,5 Дж/(кг К);

для метана = = 519,8 Дж/(кг К);

для водорода = = 4124,7 Дж/(кг К).

Суммируя все ранее сказанное, можно написать «формулу цепочки»

(15)

где - теплоемкости газов.

Приведение объема газа к нормальным условиям и подсчет плотности р в зависимости от р и Т графически легко осуществ­ляются с помощью номограмм.

2. Законы идеальных газов.

Некоторые экспериментально установленные факты, много­кратно проверенные опытом, получили название основных газовых законов. Впоследствии развившаяся молекулярно-кинетическая теория газов дала возможность вывести эти же законы ана­литически. Знание этих законов позволяет производить анализ так называемых термодинамических процессов.

Закон Бойля – Мариотта. Из кинетической тео­рии газов известно, что давление р может быть выражено формулой

(13)

где т - масса молекулы;

п - число молекул;

- скорость молекул.

Массу молекул в единице объема (т п) можно представить как величину плотности, т.е. , где g - ускорение силы тяжести. Имея в виду, что (где - удельный объем газа), получим:

откуда

(14)

При неизменной скорости движения молекул, что соответст­вует значению Т = const, будем иметь = const. Это позволяет написать:

, (15)

т. е. расширяя или сжимая газ при постоянной температуре, произведение давления газа на его объем остается неизменным, откуда

. (16)

Это соотношение впервые было получено экспериментально Бойлем (1662 г.), а впоследствии также и Мариоттом (1676 г.), которое может быть сформулировано следующим образом: при неизменной температуре Т = const) давление газа изменяется обратно пропорционально изменению объема. Этот закон спра­ведлив для любых значений объемов газа, в том числе и для удель­ных объемов, а это означает, что

. (17)

Формула (17) позволяет считать, что при неизменной темпе­ратуре плотность газа изменяется прямо пропорционально давле­нию.

Уравнение (15) в системе р - координат представляет собой кривую второго порядка, равнобокую гипербо­лу.

Закон Гей-Люссака. Экспериментально доказано, что все газы при нагревании расширяются на одну и ту же величину, равную , с повышением темпера­туры на 1°С.

Из этого закона вытекает весьма важное следствие.

При нагревании или охлаждении газа при неизменном давлении объем его изменяется (увеличивается при нагревании и уменьша­ется при охлаждении) прямо пропорционально изменению абсо­лютных температур.

. (18)

Полученная связь справедлива для любого количества газа, в том числе и для 1 кг газа. Тогда

, (19)

т. е. при неизменном давлении плотность газа изменяется обратно пропорционально абсолютным температурам. Из формулы (21) следует

(19a)

т. е. при р = const произведение плотности газа на абсолютную температуру есть величина постоянная.

Закон Шарля. Все газы в процессе их нагревания или охлаждения в условиях неизменного объема изменяют свое дав­ление на от своего первоначального значения давления.

Следствием этого закона является следующее положение. По мере нагревания или охлаждения газа при = const давление его изме­няется прямо пропорционально изменению абсолютных темпера­тур.

По аналогии с предыдущим выводом можно написать

(20)

Закон Авогадро. При одинаковых давлениях и темпе­ратурах в равных объемах двух или нескольких газов содержится одинаковое число молекул. Возьмем два равных объема V двух разных газов. Пусть в первом из них содержится всего молекул при числе молекул в единице объема этого газа, равном . Анало­гично для второго газа имеем N₂ и п₂. Массы молекул и давления газов равны соответственно Т_1, р_1, Т_2, р₂. Если допустить, что давления газов одинаковы, т. е. р₁ = р₂, то

. (21)

При одинаковых температурах кинетическая энергия поступа­тельного движения молекул одинакова, т. е.

. (22)

Тогда

(23)

откуда

Умножая обе части уравнения на получим

N₁ = N₂. (24)

Известно, что каждый газ характеризуется определенной мо­лекулярной массой , которая часто именуется грамм-молекулой или килограмм-молекулой по массе (последняя в 1000 раз больше первой).

Объем указанной массы газа составляет соответственно грамм или килограмм-моль газа по объему.

Авогадро определил число молекул в грамм-молекуле (грамм-моле):

N = 6,02510²³.

Объем одного килограмм-моля газа, или, что одно и то же, объем килограмм-молекулы любого газа, взятого в одних и тех же условиях, есть величина постоянная. Так, например, при нормальных физических условиях р = 101 325 Н/м² и t = 0°С этот объем равен 22,4 м³ для любых газов и не зависит от природы этих газов, а при нор­мальных технических условиях составляет 24,4м³.

Таким образом, известные газовые законы являются частными случаями, вытекающими из общего уравнения состояния.

3. Уравнение состояние для смеси идеальных газов.

Все зависимости, полученные выше для идеальных газов, справедливы и для их смесей, если в них подставлять газо­вую постоянную, молекулярную массу и теплоемкость смеси.

Закон Дальтона. В инженерной прак­тике часто приходится иметь дело с газо­образными веществами, близкими по свойствам к идеальным газам и пред­ставляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые сме­си. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и па­ровых котлов, влажный воздух в сушиль­ных установках и т. п.

Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси иде­альных газов равно сумме парциальных давлений всех входящих в нее компо­нентов:

(25)

Парциальное давление p_i - давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.

Способы задания смеси. Состав га­зовой смеси может быть задан массовы­ми, объемными или мольными долями.

Массовой долей называется отношение массы отдельного компонента Mi к массе смеси М_см:

(26)

Очевидно, что и .

Массовые доли часто задаются в процентах. Например, для сухого воздуха

Объемная доля представляет собой отношение приведенного объема газа V к полному объему смеси V_см:

(27)

Приведенным называется объем, который занимал бы компонент газа, если бы его давление и температура равня­лись давлению и температуре смеси.

Для вычисления приведенного объема запишем два уравнения состоя­ния i-го компонента:

, (28)

(29)

Первое уравнение относится к состоянию компонента газа в смеси, когда он имеет парциальное давление , и занимает пол­ный объем смеси, а второе уравнение - к приведенному состоянию, когда давле­ние и температура компонента равны, как и для смеси, р и Т.

откуда . Объемные доли также часто задаются в процентах. Для воздуха

Иногда бывает удобнее задать со­став смеси мольными долями. Моль­ной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N

Пусть газовая смесь состоит из N молей первого компонента, N молей вто­рого компонента и т. д. Число молей смеси , а мольная доля компонента будет равна

. (30)

В соответствии с законом Авогадро объемы моля любого газа при одинако­вых р и T, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приве­денный объем любого компонента может быть вычислен как произведение объема моля на число молей этого компо­нента, т. е. , а объем смеси - по формуле . Тогда , и, следовательно, задание смеси идеальных газов мольными долями рав­нозначно заданию ее объемными долями.

Газовая постоянная смеси газов.

Для смеси справедливо такое соотношение

, (31)

где

(32)

Смесь идеальных газов также подчиняется уравне­нию Клапейрона.

Поскольку то из (32) следует, что газовая постоянная смеси [Дж/(кгК)] имеет вид

(33)

Кажущаяся молекулярная масса смеси.

Выразим формально газовую постоянную сме­си R_см, введя кажущуюся молекулярную массу смеси _см:

(34)

Сравнивая правые части соотношений (33) и (34), найдем

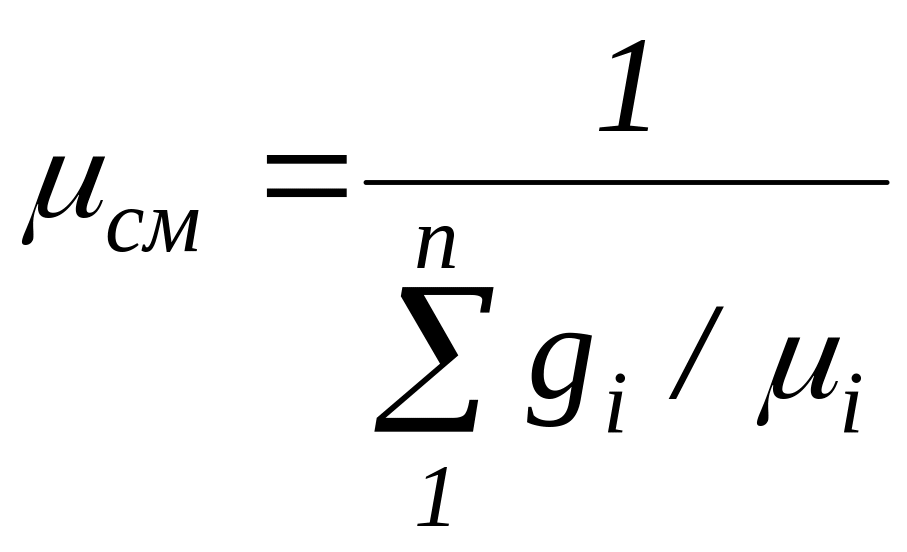(35)

Из определения массовых долей следует, что

Просуммировав это соотношение для всех компонентов и учитывая, что , получим выражение для кажущейся молекулярной массы смеси, заданной объемными долями:

(36)

Соотношение между объемными и массо­выми долями. Учитывая (36), получаем

(37)

Поскольку то

(38)

Разделив числитель и знаменатель этой формулы на массу смеси М, получим

(39)

Теплоемкость смесей идеальных га­зов. Если смесь газов задана массовыми долями, то ее массовая теплоемкость с определяется как сумма произведений массовых долей на массовую теплоем­кость каждого компонента, т. е.

; (40)

При задании смеси объемными до­лями объемная теплоемкость смеси

; (41)

Аналогично мольная теплоемкость смеси равна произведению объемных до­лей на мольные теплоемкости составляю­щих смесь газов:

; (42)

ЛЕКЦИЯ 3. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ (4)

План

1. Понятия о внутренней энергии, работе расширения и теплоте.

2. Аналитическое выражение первого закона термодинамики

Литература:

1. Теплотехника / Баскаков А. П., Берг В. В., Вит О. К. и др. - М.: Энергоиздат, 1991.- 224 с.

2. Теплотехника / Хазен М. М., Матвеев Г Д., Грицевский М. Е. и др.- М.: Высш. школа,1981.- 480 с.

3. Швец И.Т., Толубинский В.И., Алабовский А.Е. и др. Теплотехника - К.: "Вища школа", Головное изд - во, 1976.- 517 с.

4. Нащокин В.В. Техническая термодинамика и теплопередача. Учебн. Пособие для вузов.- 3-е изд.- М.: Высшая школа, 1980.- 469 с.

5. Кафаров В.В. Основы массопередачи. Учеб. пособие для вузов.- М.: Высшая школа, 1972.- 494 с.

1. Понятия о внутренней энергии, работе расширения и теплоте.

Внутренняя энергия системы включает в себя:

• кинетическую энергию поступательного, вращательного и колебательного движения частиц;

• потенциальную энергию взаимодействия частиц;

• энергию электронных оболочек атомов;

• внутриядерную энергию.

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Поэтому в даль­нейшем под внутренней энер­гией будем понимать энергию хаотиче­ского движения молекул и атомов, вклю­чающую энергию поступательного, вращательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.

Кинетическая энергия молекул явля­ется функцией температуры, значение потенциальной энергии зависит от сред­него расстояния между молекулами и, следовательно, от занимаемого газом объема V, т.е. является функцией V. Поэтому внутренняя энергия U есть функ­ция состояния тела.

Для сложной системы она определя­ется суммой энергий отдельных частей, т. е. обладает свойством аддитивности.

, кДж/кг (1)

Данная величина называемая удельной внутренней энер­гией (Дж/кг), представляет собой внутреннюю энергию единицы массы ве­щества.

В дальнейшем для краткости будем называть величину и просто внутренней энергией. Поскольку внутренняя энергия есть функция состояния тела, то она мо­жет быть представлена в виде функции двух любых независимых параметров, определяющих это состояние:

; ;

Ее изменение в термодинамическом процессе Аи не зависит от характера процесса и определяется только началь­ным и конечным состояниями тела: , где - значение внутренней энергии в начальном состоянии, а - в конечном. Математически это означает, что бесконечно малое измене­ние внутренней энергии du есть полный дифференциал и; если выразить внутрен­нюю энергию в виде функции удельного объема и температуры, то

(2)

Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодей­ствия между молекулами, не зависит от объема газа или давления , a определяется только его температурой, поэтому производная от внутренней энергии идеального газа по температуре есть полная производная:

(3)

Для задач технической термодинами­ки важно не абсолютное значение внут­ренней энергии, а ее изменение в различ­ных термодинамических процессах. По­этому начало отсчета внутренней энер­гии может быть выбрано произвольно. Например, в соответствии с международ­ным соглашением для воды за нуль при­нимается значение внутренней энергии при температуре 0,01 °С и давление 610,8 Па, а для идеальных газов - при 0 °С вне зависимости от давления.

Работа в термодинамике, так же как и в механике, определяется произведени­ем действующей на рабочее тело силы на путь ее действия.

Рассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F (рис. 1). Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давлении р, оказываемого на него средой. Газ дев­ствует на каждый элемент оболочки dF с силой, равной pdF и, перемещая ее по нормали к поверхности на расстояние dn совершает элементарную работу pdFdn Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя данное выражение по всей поверхности F оболочки:

(4)

Рис.1. К определению работы расширения

Из рис.1 видно, что изменение объема dV выражается в виде интеграла по поверхности: , следовательно

(5)

При конечном изменении объема работа против сил внешнего давления, называемая работой расширения, равна

(6)

Из (6) следует, что и всегда имеют одинаковые знаки:

• если (dV>0, то и >0, т.е. при расширении работа тела положительна при этом тело само совершает работу

• если же dV <0, то и <0, т. е. при сжатии работа тела отрицательна: это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне.

Единицей измерения работы в СИ яв­ляется джоуль (Дж).