- •Модуль 1
- •Модуль 3
- •Модуль 4
- •Содержательный модуль 1 «термодинамика»
- •1. Предмет и метод термодинамики
- •2. Термодинамическая система
- •3. Параметры состояния рабочего тела.
- •Отнеся работу расширения к 1 кг массы рабочего тела, получим
- •Лекция 4. Второй закон термодинамики (4) план
- •1. Энтропия
- •Из уравнения (2) следует, что в равновесном процессе
- •2. Общая формулировка второго закона
- •3. Прямой цикл карно
- •4. Обобщенный (регенеративный) цикл карно
- •5. Обратный цикл карно
- •7. Статистическое толкование второго
- •8. Эксергия
- •1. Изохорный процесс
- •При переменной теплоемкости
- •2. Изобарный процесс
- •3. Изотермический процесс
- •4. Адиабатный процесс.
- •5. Политропный процесс
- •Содержательный модуль 2 «реальные газы. Водяной пар»
- •Лекция 6. Термодинамические процессы
- •Реальных газов (4)
- •Содержательный модуль 3 «теплопередача» лекция 7. Основные случаи теплообмена. Теплопроводность (4) план
- •1. Определения
- •3. Теплоотдача между стенкой и жидкостью
- •4. Теплопередача через плоскую стенку
- •5. Теплопередача через цилиндрическую стенку
- •Лекция 8. Теплообмен соприкосновением (4) план
- •2. Вычисление коэффициентов теплоотдачи
- •3. Эмпирические формулы
- •5. Теплопередача к кипячей жидкости.
- •Лекция 9. Теплообмен излучением план
- •1. Физические законы излучения
- •3. Излучение газов
- •Лекция 10. Теплообменный аппарат план
- •1. Основные определения
- •2. Определение поверхности нагрева теплообменного аппарата. Средняя разность температур
- •Содержательный модуль 4 «топливо» лекция. Топливо и основы теории горения
- •1. Состав топлива.
- •2. Характеристика топлива
- •3. Моторные топлива для поршневых двс
- •4. Котельный агрегат и его элементы.
- •5. Вспомогательное оборудование котельной установки.
- •6. Тепловой баланс котельного агрегата.
- •Тема 15. Топочные устройства.
- •15.1. Топочные устройства.
- •15.2. Сжигание топлива.
- •15.3. Теплотехнические показатели работы топок.
- •Тема 16.Горение топлива.
- •16.1. Физический процесс горения топлива.
- •16.2. Определение теоретического и действительного расхода воздуха на горение топлива.
- •16.3. Количество продуктов сгорания топлива.
- •Тема 17. Компрессорные установки.
- •17.1. Объемный компрессор.
- •17.2. Лопаточный компрессор.
- •Литература
- •Теплотехника / Баскаков а. П., Берг в. В., Вит о. К. И др. - м.: Энергоиздат, 1991.- 224 с.
- •Теплотехника / Хазен м. М., Матвеев г д., Грицевский м. Е. И др.- м.: Высш. Школа,1981.- 480 с.
- •Швец и.Т., Толубинский в.И., Алабовский а.Е. И др. Теплотехника - к.: "Вища школа", Головное изд - во, 1976.- 517 с.
5. Теплопередача к кипячей жидкости.
При расчете поверхности нагрева котла передачей тепла на внутренней стороне, т. е. от стенки к кипящей жидкости, можно пренебречь, так как наибольшим термическим сопротивлением оказывается сопротивление на наружной стороне, т. е. от газов к стенке; однако величина этого коэффициента теплоотдачи важна для определения температуры стенки.
При кипении в трубках паровых котлов коэффициент теплоотдачи сильно зависит от характера движения пароводяной смеси.
Существенное значение для расчета поверхности нагрева имеет коэффициент теплоотдачи при кипении в испарителях и аналогичной химической аппаратуре, где отдельные термические сопротивления соизмеримы.
При кипении жидкостей передача тепла от стенки происходит к близлежащему слою жидкости, который несколько перегревается и в свою очередь отдает тепло пузырькам пара, зарождающимся в отдельных точках поверхности нагрева - в так называемых очагах кипения. Образующиеся пузырьки пара поднимаются в жидкости, причем их объем возрастает.
При кипении жидкостей в большом свободном объеме для невысокой тепловой нагрузки (для воды это соответствует ∆t < 5° С), когда образующиеся пузыри (пузырчатое кипение) пара мало влияют на интенсивность теплообмена, можно пользоваться формулами для естественной конвекции (28) и (29).
Чем больше тепловая нагрузка поверхности нагрева при кипении, т. е. чем больше образуется пузырей пара, тем интенсивнее происходит перемешивание жидкости и тем больше будет коэффициент теплоотдачи.
При нагрузке выше q = 8 000 вт /(мг • град) для воды можно принять:
![]() (35)
(35)
где С - постоянная, зависящая от давления р.
По исследованиям С. С. Кутателадзе (ЦКТИ) при давлении до 10 бар
С = 2,6р0,4. (36)
При более высоких давлениях рост С при увеличении р замедляется.
При кипении воды в трубах в интервале давлений от 1 до 40 бар можно пользоваться формулой
![]() (37)
(37)
где q — плотность теплового потока.
В формулах 35…37 абсолютное давление р измерено в барах. Значения а и q измерены соответственно в единицах Вт/(м2 ▪град) и Вт/м2.
Так как q в свою очередь определяется значением а и разностью температур, то задача в этом случае решается подбором.
По достижении некоторого критического перепада температур между стенкой и жидкостью коэффициент теплоотдачи резко падает, так как образующаяся на поверхности сплошная пленка пара (пленочное кипение) мешает подходу к стенке новых масс жидкости. Для воды при атмосферном давлении критический перепад температур, при котором ядерное кипение переходит в пленочное, составляет около 25° С, а соответствующая критическая нагрузка — около 1 млн. вт1м2.
Лекция 9. Теплообмен излучением план
1. ФИЗИЧЕСКИЕ ЗАКОНЫ ИЗЛУЧЕНИЯ
2. РАЗЛИЧНЫЕ СЛУЧАИ ТЕПЛООБМЕНА ИЗЛУЧЕНИЕМ
3. ИЗЛУЧЕНИЕ ГАЗОВ
1. Физические законы излучения
В областях теплотехники, где приходится иметь дело с высокими температурами, теплообмен излучением имеет первенствующее значение. Интенсивность теплообмена излучением превосходит в этих случаях другие виды теплообмена; поэтому техника котлостроения идет по пути создания конструкций агрегатов, максимально использующих этот вид теплообмена.
Одна из особенностей теплообмена излучением заключается в том, что он сопровождается двойным преобразованием энергии. Один раз это преобразование происходит тогда, когда тело испускает во внешнее пространство лучи; при этом теплота, теряемая телом, превращается в лучистую энергию; второе преобразование происходит, когда лучи достигают другого тела и лучистая энергия снова переходит в теплоту, воспринимаемую этим телом.
Излучение есть результат внутриатомных процессов. В настоящем разделе нас будет интересовать расчетная сторона теплообмена излучением, и поэтому мы не будем рассматривать физическую природу лучистой энергии. Отметим лишь, что тепловые лучи представляют собой электромагнитные колебания с длиной волны λ от 0,76 до 353 мк (это так называемое инфракрасное излучение).
Различные тела обладают различной способностью к поглощению лучей и излучению их. Тело, способное полностью поглощать тепловые лучи любой длины волны и обладающее максимальной способностью к излучению (оба эти свойства связаны между собой), называется черным или абсолютно черным телом.
В природе имеются тела, близкие по свойствам к абсолютно черному телу: так, черное сукно поглощает 98% падающего на него излучения; черный бархат 99,5%.
Нагретое абсолютно черное тело испускает лучи, перекрывающие всю область длин волн (сплошной спектр). Если каким-либо образом отделить лучи с разными длинами волн друг от друга и измерить энергию каждого луча, окажется, что распределение энергии вдоль спектра неравномерно, а именно; сначала по мере увеличения длины волны энергия лучей возрастает, а затем падает. Кроме того, для луча одной и той же длины волны энергия увеличивается по мере увеличения температуры тела, испускающего лучи. Энергию, излучаемую телом, измеряют плотностью теплового потока, приходящегося на единицу длины волны, и называют эту величину интенсивностью излучения. Она обозначается Iλ.
На рис. 1 дана зависимость интенсивности излучения Iλ от длины волны и температуры:
Iλ=f(λ, T) (1)
Единицей измерения для Iλ в системе МКС служит вт/(м2 ▪м) - Вт/м3.
|
|
Рис.1. Зависимость интенсивности излучения от длины волны и температуры |
Рис.2. Схема осуществления абсолютно черного тела. |
Выделим узкую часть спектра, заключающую длины волн от λ до λ + dλ.. Тогда энергия dE лучей этой части спектра (заштрихованная площадь на рис. (1), отнесенная к единице излучающей поверхности и к единице времени, составит:
dE = Iλ dλ (2)
При малой величине интервала длин волн dλ можно считать, что вся эта энергия излучается в виде лучей одной определенной длины волны. Такое излучение называется монохроматическим.
Распределение энергии в спектре абсолютно черного тела может быть экспериментально изучено следующим образом.
Если взять полое сферическое тело, в одном месте стенки которого находится узкое отверстие, оно (отверстие) может служить образцом абсолютно черного тела (рис.2). Действительно, любой луч, падающий через это отверстие в полость тела, будет до тех пор отражаться от поверхности и вновь на нее падать, пока целиком не поглотится. Следовательно, площадь отверстия играет роль черного тела по отношению к падающему на нее излучению. С другой стороны, если нагреть полое тело, например, при помощи электрического нагревателя, то из отверстия в стенке будет исходить поток лучистой энергии. Спектр излучения при этом по своему характеру будет весьма близок спектру абсолютно черного тела.
Теоретически распределение энергии в спектре черного тела было изучено Планком при помощи введенной им в науку теории квант, согласно которой лучистая энергия представляет собой прерывистый поток отдельных порций энергии, названных квантами.
На основании теории квант Планк нашел соотношение, определяющее интенсивность излучения черного тела (закон Планка):
 (3)
(3)
где с1 и с2 - постоянные величины;
е - основание натуральных логарифмов.
Это соотношение представлено графически на рис.1.
Интегрируя уравнение (2) в пределах длин волн от 0 до оо, найдем энергию излучения абсолютно черного тела. Она составляет:
![]() (4)
(4)
Тепловые лучи не охватывают всех длин волн от 0 до оо. Однако интегрирование в этих пределах допустимо вследствие пренебрежимо малого теплового эффекта лучей с остальными длинами, и делается это для удобства интегрирования.
Подставляя вместо Iλ его значение из (3) и произведя интегрирование, получим:
![]() (5)
(5)
здесь
![]() -
постоянная излучения; индекс «ч»
показывает, что
она относится к абсолютно черному телу,
для которого
-
постоянная излучения; индекс «ч»
показывает, что
она относится к абсолютно черному телу,
для которого
![]() =
4,88▪10-8
ккал/(м2▪ч▪град4)
=
4,88▪10-8
ккал/(м2▪ч▪град4)
= 5,69▪10-8 Вт/(м2▪град4) (6)
В формуле (5) Е измеряют системной единицей вт/м2 или внесистемной единицей ккал/(м3 ▪ ч); коэффициент излучения, как видно, измеряется системной единицей вт/(м2 град) или внесистемной ккал1(мг ▪ч▪град).
Уравнение (5) носит название уравнения Стефана - Больцмана. Экспериментально оно было получено Стефаном, а теоретически - Больцманом.
Для упрощения вычислений формулу (5) представляют в таком виде
![]() (7)
(7)
здесь Сч - также константа излучения, равная 5,69 вт/(м2 ▪град4).
Излучение реальных тел в той или иной степени отклоняется от закона Стефана - Больцмана. Действительная форма кривой интенсивности излучения может отличаться от формы, соответствующей уравнению (3); для некоторых длин волн интенсивность излучения может быть ниже, чем в абсолютно черного тела, а для других длин волн излучение может вообще отсутствовать. Эти свойства видны в спектре, изображенном на рис. 3. Заштрихованная часть площади, лежащей под кривой спектра абсолютно черного тела, относится к длинам волн, излучаемых реальным телом; незаштрихованная показывает степень ослабления излучения или относится к длинам волн, отсутствующим в излучении данного тела.
|
Рис3. Прерывистый спектр излучения. |
Для упрощения практических расчетов введено понятие о так называемом «сером» излучении или сером теле. Под серым излучением понимается такое излучение, которое аналогично «черному» имеет сплошной спектр, но интенсивность лучей для каждой длины волн при любой температуре в определенное число раз меньше, чем у черного тела.
В таком случае подсчет общей энергии излучения можно произвести по формуле (7-7), но уже с меньшим, чем у черного тела, значением С:
![]() (8)
(8)
где С - коэффициент излучения данного серого тела (рис. 4).
Излучение большинства твердых тел можно считать близким к «серому» излучению; при этом коэффициент С находится из опыта. Ввиду некоторого отклонения излучения реальных тел от серого излучения коэффициент С может меняться с температурой.
Закон Ламберта. Поверхность каждого тела излучает энергию по всем направлениям, но не одинаково интенсивно.
Наибольшее количество энергии несут лучи, направленные по нормали к излучающей поверхности.
В других направлениях количество излучаемой энергии меньше и выражается законом Ламберта: количество энергии, излучаемой в направлении, составляющем угол с нормалью, пропорционально cos φ. Если обозначить количество энергии, посылаемое по нормали, Ен, то по направлению, составляющему с нормалью угол φ, количество излученной энергии (рис. 5) составит:
![]() (9)
(9)
Закон Кирхгофа. Когда луч достигает поверхности твердого непрозрачного (т. е. не пропускающего лучи) тела, то он частично поглощается, частично же луч отражается и рассеивается.
|
|
|
Рис. 5. Излучение под углом φ к нормали (к закону Ламберта).
|
Отражение в зависимости от свойств поверхности может быть правильным или диффузным {рассеивание). В первом случае поверхность называется зеркальной; отраженный и падающий лучи будут лежать в одной плоскости, нормальной к поверхности отражения. Во втором случае отраженные лучи распространяются по всем направлениям. Поверхность отражения в этом случае называется матовой.
Если энергию падающего луча принять за единицу и обозначить долю энергии, поглощенную непрозрачным телом, буквой А, а буквой R - отраженную, то
A+R=1 (10)
Величина А характеризует лучепоглощательную способность тела и называется коэффициентом поглощения. Для черного тела, очевидно, А = 1 и R = 0. Напомним, что излучательную способность тела характеризует коэффициент излучения С.
Между способностями тела к излучению и поглощению существует зависимость, известная под названием закон Кирхгофа: отношение излучательной способности тела к его поглощательной способности есть величина постоянная для всех твердых тел. Для излучения серых тел закон Кирхгофа запишется так:
![]() = const.
(11)
= const.
(11)
Значение постоянной может быть определено из приведенной зависимости, если ее написать для черного тела, для которого Сч, и Ач, известны:
![]() вт/(м2
•
град).
вт/(м2
•
град).
Так как согласно закону Кирхгофа
![]() (12)
(12)
С = 5,69 А вт/(м2▪град). (13)
Из уравнения (13) видно, что А и С пропорциональны друг другу, т. е. если тело обнаруживает большую способность к излучению энергии, то такую же способность оно будет проявлять и к поглощению энергии, и наоборот.
Закон Кирхгофа верен и для монохроматического излучения. В этом случае он математически выражается следующим образом:
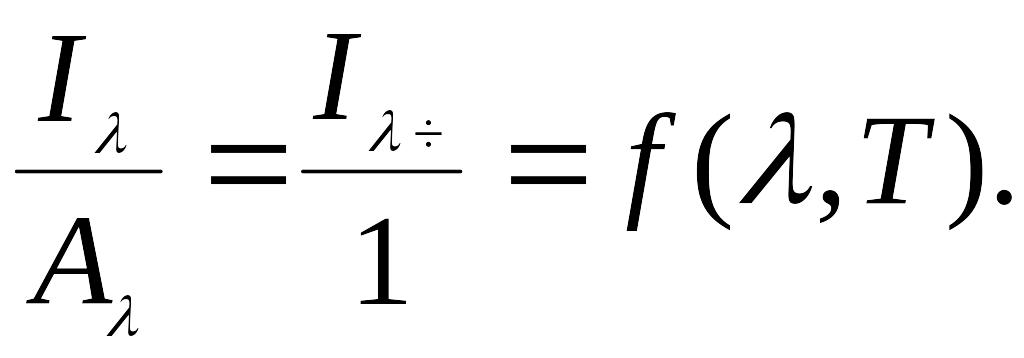
Если в пропорции (12) переставить средние члены, то она принимает вид:
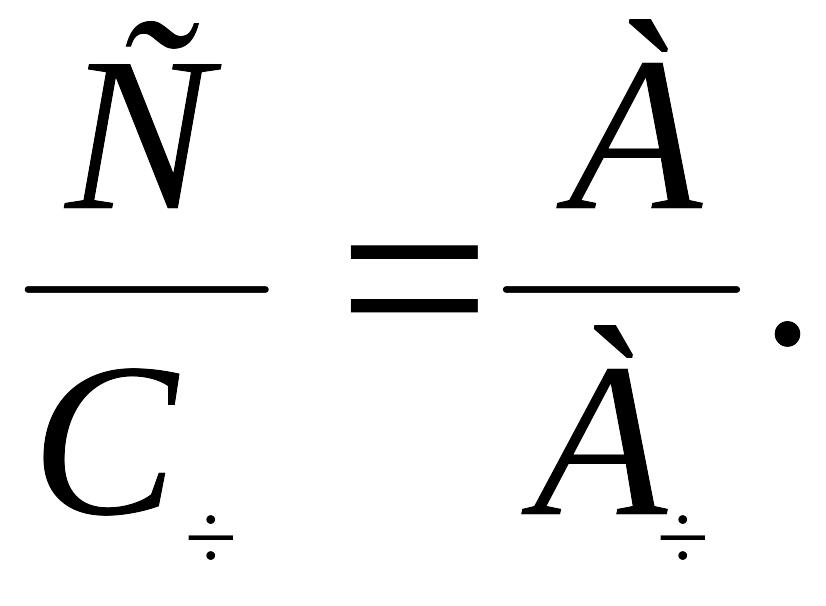
Полученные два отношения показывают, какую долю составляют способность данного тела к поглощению и к излучению энергии по сравнению с той же способностью абсолютно черного тела. Эта доля обозначается буквой а и называется коэффициентом черноты данного тела.
Итак,
![]() и
и
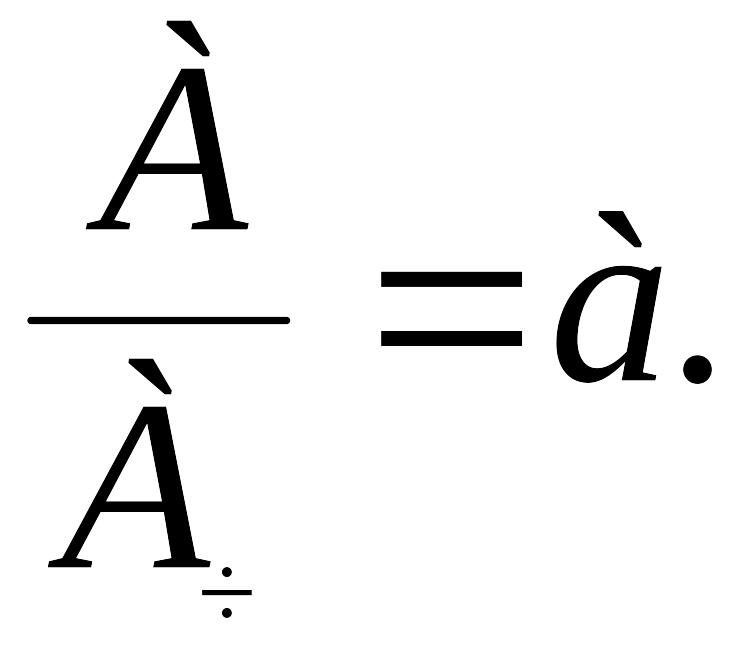
Так как Ач = 1, то
а=А,
т. е. коэффициент черноты любого тела равен его коэффициенту поглощения.
2. РАЗЛИЧНЫЕ СЛУЧАИ ТЕПЛООБМЕНА ИЗЛУЧЕНИЕМ
Случай теплообмена между двумя поверхностями, расположенными параллельно или концентрически по отношению друг к другу, часто встречается в технических расчетах. Многие случаи действительного теплообмена могут быть приближенно сведены к этим двум случаям.
|
Рис. 6. Теплообмен излучением между двумя параллельно расположенными поверхностями |
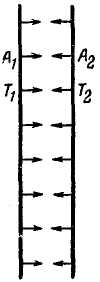
Пусть имеются две очень большие поверхности, расположенные параллельно и на небольшом расстоянии одна от другой (рис. 6) так, чтобы все излучение, исходящее от одной из них, падало на другую.
Обозначим соответственно: Q1 и Q2 - полные потоки энергии, исходящие от первой и второй поверхностей; С1 и С2 - их коэффициенты излучения; Т1 и Т2 - температуры.
Найдем Q1 и Q2. Количество энергии, излучаемое первой поверхностью, составляется из собственного излучения, определяемого по закону Стефана — Больцмана, и отраженной энергии, полученной от второго тела. Отсюда
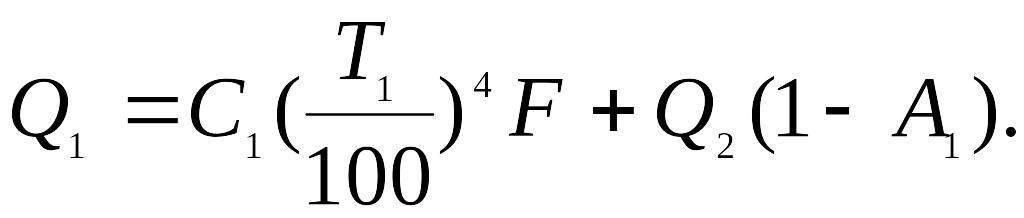 (а)
(а)
Первый член суммы, стоящей в правой части равенства, как видно, определяется формулой (8). Второй член определяется следующим образом: если Q2 — полная энергия, излучаемая вторым телом и падающая на первое тело, то количество Q2A1 ее будет первым телом поглощено, остальное же - отражено. Последнее, очевидно, составит:
Q2 - Q2А1 = Q2 (1 - А1)- Таким же образом может быть вычислена энергия, излучаемая вторым телом. Она составляет:
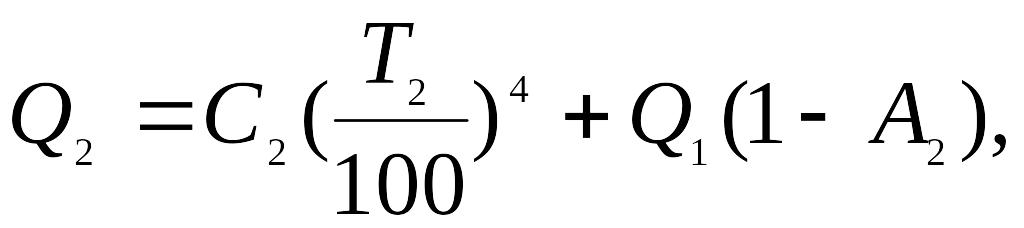 (б)
(б)
где первый член выражает энергию, излучаемую вторым телом и определяемую по закону Стефана - Больцмана, а второй член - энергию, отраженную вторым телом из того количества, которое падает на него от первого тела.
Разность величин (а) и (б), очевидно, есть количество энергии, воспринятое вторым телом (Т1 > Т2) в результате теплообмена излучением; тогда
Q = Q1 - Q2 (в)
Решая два уравнения (а) и (б) с двумя неизвестными Q1 и Q2, можно найти их, а после этого определить и Q. Такое решение после замены:
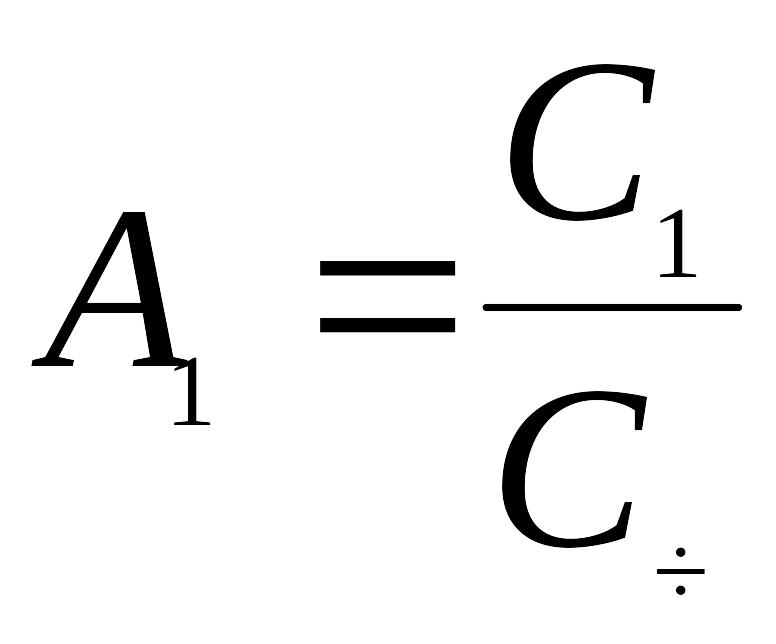 и
и
![]()
дает:
 (15)
(15)
Коэффициент в уравнении (15) обозначается:

и называется приведенным коэффициентом излучения.
Значения Q и С здесь измерены соответственно или в системных единицах: Вт-Вт/(мг ▪град4).
Таким образом, можно сказать, что при теплообмене излучением двух параллельных друг другу поверхностей количество энергии, которым они обмениваются, может быть определено по формуле Стефана - Больцмана, если для обеих поверхностей взять один и тот же коэффициент излучения, равный приведенному коэффициенту излучения [С].
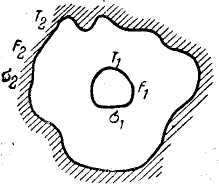
Рассмотрим теперь теплообмен излучением двух поверхностей, расположенных одна в другой. Будем при этом исходить из того, что внутренняя поверхность выпуклая и не образует впадин, что исказило бы результаты выводов.
Пусть на рис. 7 изображены две такие поверхности и для них Q1, F1, А1, C1, Т1 соответственно - полное количество излучаемой энергии, поверхность, коэффициенты поглощения и излучения и температура первой поверхности; Q2, F2, A2, С2, Т2 - то же для второй поверхности.
Количество тепла, передаваемое излучением, определится как разность потоков энергии, исходящих от каждой из поверхностей.
Первая поверхность испускает и отражает количество энергии Q1. Если эта поверхность невогнутая, то все лучи, исходящие от нее, падают на вторую поверхность. Вторая поверхность испускает и отражает количество энергии Q2, но из всего этого количества энергии только некоторая доля β попадает на первое тело. Остальное количество лучистой энергии Q2 (1- β) падает на свою же поверхность F%. Отсюда переданное тепло определится как разность:
Q=Q1 - Q2β. (г)
Входящие в уравнение (г) величины Q1 и Q2 могут быть определены из следующих соображений.
|
Рис. 7. Теплообмен излучением между двумя поверхностями, расположенными одна в другой. |
Количество энергии, излучаемое первой поверхностью, составляется из собственного излучения, определяемого по формуле Стефана - Больцмана, и энергии, которая отражается в результате падения излучения от второй поверхности. Эта отраженная энергии вычисляется так: поверхность F2 посылает на F1 количество лучистой энергии Q2β. Часть ее A1Q2β поглощается первой поверхностью, а остальная часть Q2β - A1Q2β (1 - А1) Q2β излучается обратно на поверхность F2. Таким образом, общее количество энергии, излучаемое первой поверхностью, определится выражением
![]() (д)
(д)
Количество
лучистой энергии Q2,
посылаемое
поверхностью
F2,
найдется
так: собственное излучение определяется
по
формуле Стефана - Больцмана и равно
![]() из
количества энергии, посылаемого
поверхностью F1,
количество
Q1A1
поглощается
поверхностью F2,
а
остальная часть
Q1
-
Q1A1
=
Q1
(1 - A2)
отражается обратно на поверхность F1.
Кроме
того, как уже было сказано ранее, из
общего
излучения Q2
поверхности F2
количество
Q2
(1
- Р) падает на свою же поверхность F2;
из
него часть Q2A2(1-β)
поглощается,
а остальная часть Q2
(1
- β) -
Q2A2(1-β)
=
Q2
(1
- β) (1 - A2)
отражается. Таким образом, полное
количество
энергии, исходящее от поверхности F2,
определится
выражением
из
количества энергии, посылаемого
поверхностью F1,
количество
Q1A1
поглощается
поверхностью F2,
а
остальная часть
Q1
-
Q1A1
=
Q1
(1 - A2)
отражается обратно на поверхность F1.
Кроме
того, как уже было сказано ранее, из
общего
излучения Q2
поверхности F2
количество
Q2
(1
- Р) падает на свою же поверхность F2;
из
него часть Q2A2(1-β)
поглощается,
а остальная часть Q2
(1
- β) -
Q2A2(1-β)
=
Q2
(1
- β) (1 - A2)
отражается. Таким образом, полное
количество
энергии, исходящее от поверхности F2,
определится
выражением
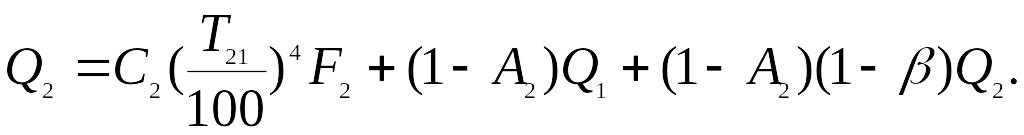 (е)
(е)
Решая два уравнения (д) и (е) с двумя неизвестными, находят Q1 и Q2.
Подставляя найденные значения в уравнение (г), вычисляют значение Q:
 (ж)
(ж)
Значения коэффициента β легко найти, рассматривая частный случай, когда температуры обеих поверхностей одинаковы; тогда по второму закону термодинамики должно быть Q = О, и из (ж) при Т1 = Т2 получается:
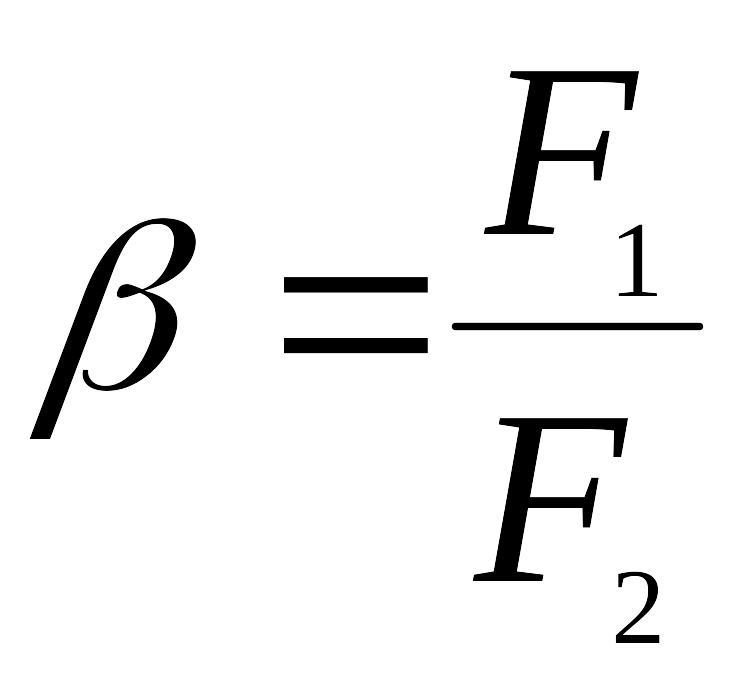
Подставляя это значение в (ж) и заменяя
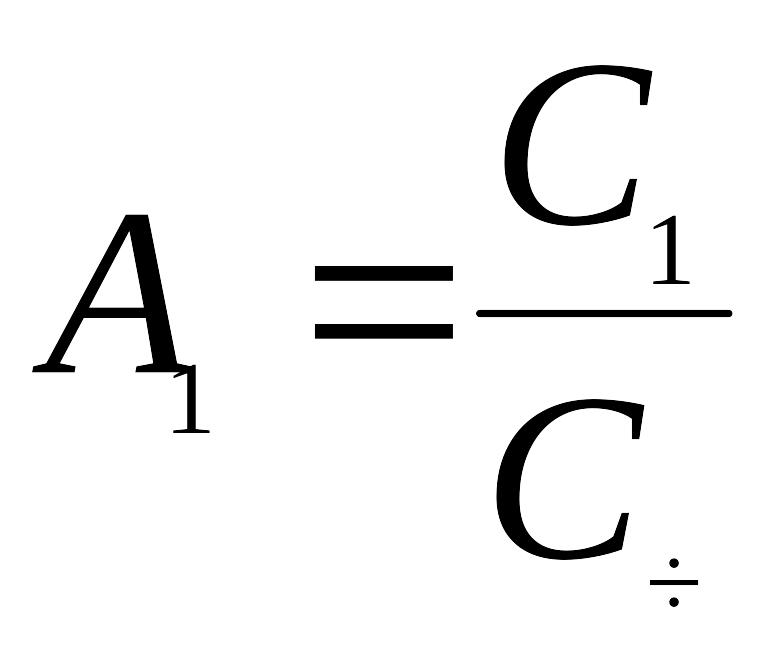 и
и
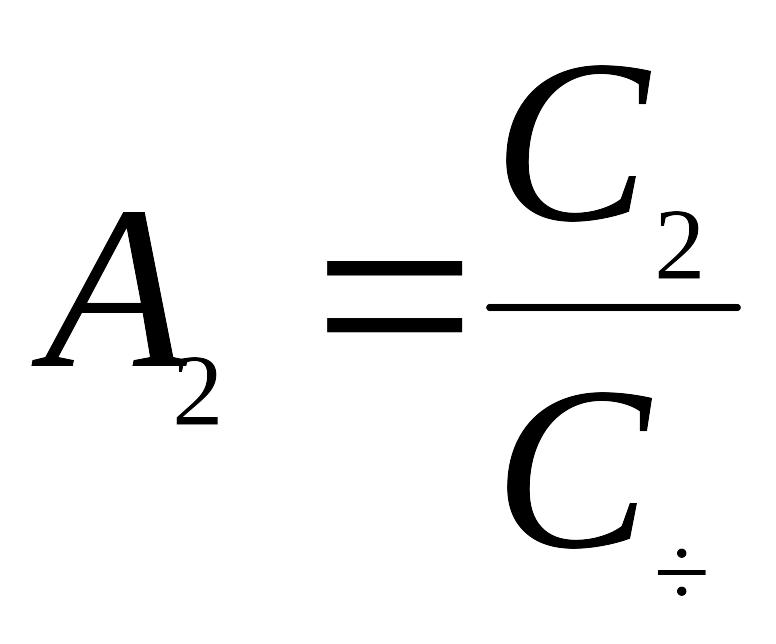
получим окончательно:
 (17)
(17)
Коэффициент в уравнении (17) обозначается:
 (18)
(18)
и называется приведенным коэффициентом излучения.
Тогда формула (17) принимает вид:
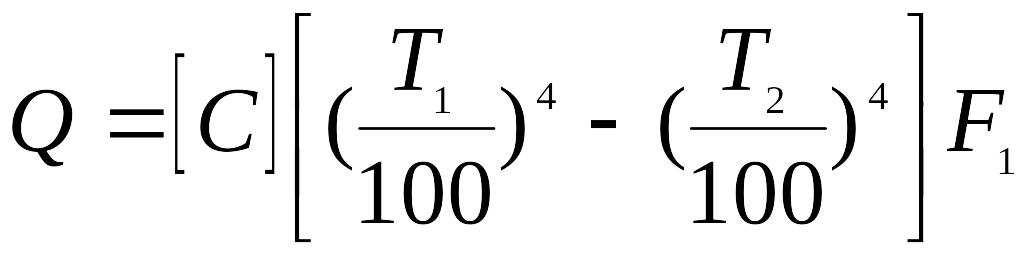 (19)
(19)
Формула для приведенного коэффициента излучения (19), строго верная для случаев двух концентрических шаров и цилиндров, практически применяется и для более общего случая, изображенного на рис. 7.
При произвольном расположении поверхностей определение количества тепла, переданного излучением одной поверхностью другой, очень сложно. Аналитическое решение может быть доведено до конца только для отдельных очень простых случаев. Общий метод решения этих задач приводится в специальных курсах. Обычно же здесь прибегают к эмпирическим формулам. Количество тепла, которое воспринимается какой-либо поверхностью, выражают формулой
![]() (20)
(20)
где С1,С2,Сч - приведенный коэффициент излучения, а Fл есть так называемая эффективная лучевоспринимающая поверхность.
Так, в тепловом расчете котла приходится вычислять эквивалентную поверхность пучка труб, воспринимающих тепло излучением из топочного пространства. Эту поверхность обычно представляют в виде произведения
![]() (21)
(21)
здесь L - длина трубы;
b- полная ширина пучка трубы;
Ψ - коэффициент, зависящий от типа пучка (шахматный, коридорный), расстояния между трубами и количества рядов труб в пучке; значения коэффициента Ψ приводятся в специальных курсах. При большом числе рядов Ψ = 1.
В начале этой лекции отмечалось, что теплообмен излучением широко используется в различных областях техники и в особенности в паровых котлах. Однако в некоторых случаях стремятся уменьшить влияние теплообмена излучением и прибегают к защите от лучистой энергии. Это имеет место, например, тогда, когда нужно оградить от действия тепловых лучей людей, работающих в цехе, где имеются поверхности с высокой температурой; в других случаях нужно оградить от лучистой энергии отдельные части машин и сооружений; от действия лучистой энергии защищают термометры, когда хотят измерить температуру какой-либо газовой среды (например, воздуха), так как при поглощении тепловых лучей ртуть в термометре дополнительно нагревается и температура ртути в этом случае не равна измеряемой температуре газа.
Во всех этих случаях прибегают к так называемым экранам, которые и предназначены для уменьшения теплообмена излучением.
Рассмотрим для примера наиболее простые случаи.
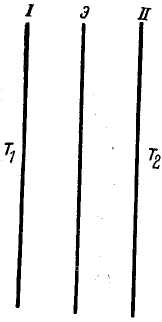
Пусть имеются две поверхности I и II, теплообмен между которыми желают уменьшить (рис. 8). Если температуры их Т1 и Т2, а коэффициенты излучения С1 = С2 (для простоты считаем их равными), удельное количество передаваемого тепла на 1 м2 поверхности в час составит:
где [С] - приведенный коэффициент излучения, определяемый по формуле (16).
|
Рис.8. Применение экрана для уменьшения теплообмена между двумя параллельно расположенными поверхностями |
Установим теперь между поверхностями экран в виде тонкого металлического листа. Температура на обеих сторонах экрана будет одинаковая Тэ, коэффициент излучения обеих поверхностей экрана для простоты также примем одинаковым и равным коэффициенту излучения поверхностей I и II. Тогда приведенный коэффициент излучения между каждой из поверхностей I и II и соответствующей поверхностью экрана будет равен [С], определяемому по формуле (16).
При рассмотрении действия экрана исходим из того, что экран, воспринимая энергию от тела I, передает ее всю телу II.
В этом случае количество тепла на 1 м2 поверхности, передаваемое излучением между телом I и экраном и между экраном и телом II, определится из уравнения
![]() (3)
(3)
Комбинируя вторую и третью части этого уравнения, можно определить:
![]()
Подставляя Т3 во вторую часть уравнения (3), вычисляем количество тепла, переданное первым телом экрану; оно будет равно количеству тепла, переданного экраном телу II. Это количество тепла составляет:
![]()
![]()
![]() (22)
(22)
Полученное уравнение (22) показывает, что при наличии одного экрана теплообмен между телами I и II уменьшается вдвое. Аналогичным образом можно найти, что если между телами I и II установить п экранов, то количество передаваемого тепла в этом случае составит:
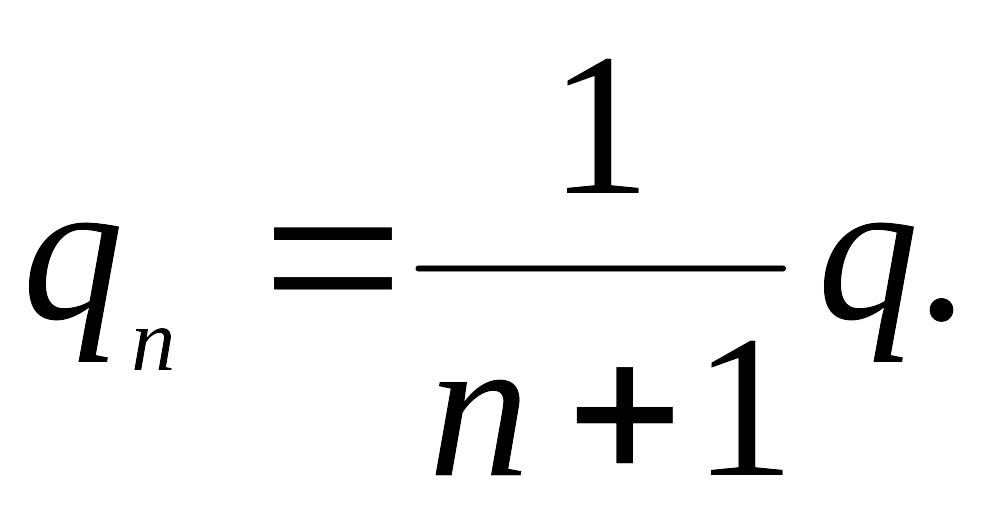
Таким образом, увеличивая число экранов, мы уменьшаем теплообмен излучением. Этим объясняется, например, что дверцы топок котлов делают из нескольких стальных листов.
Если две рассматриваемые поверхности имеют одинаковый коэффициент излучения С1 а коэффициент излучения экрана равен Сэ, то
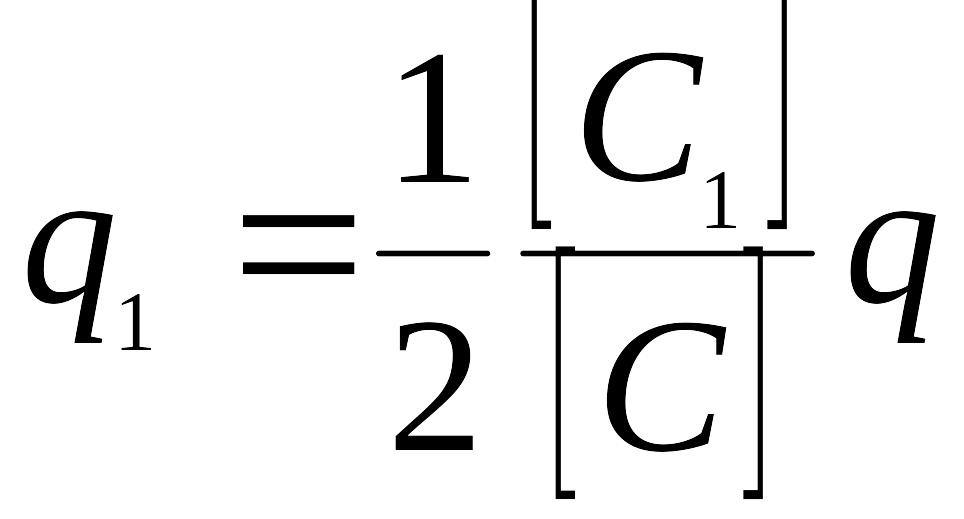 (24)
(24)
где [С] есть п р и в е д е н н ы й к о э ф ф и ц и е н т излучения между обоими телами:
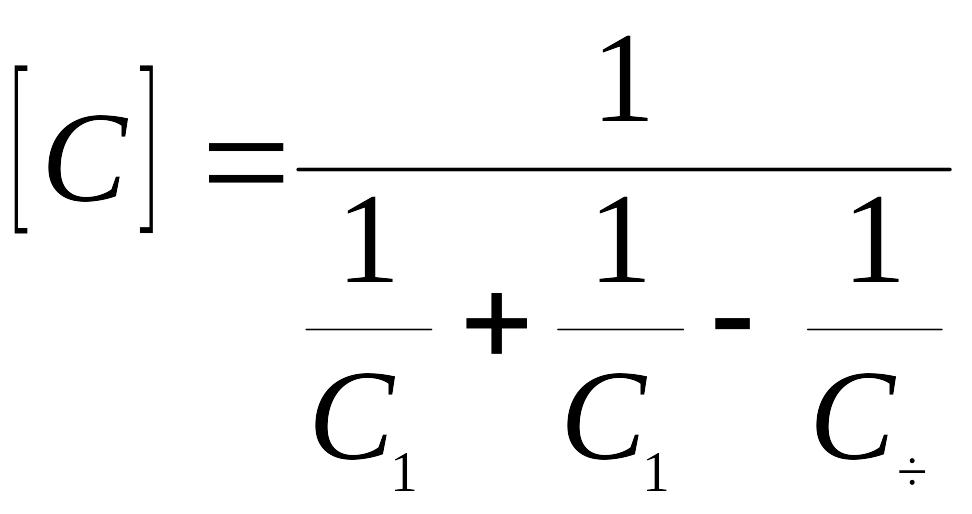
а С1 - п р и в е д е н н ы й к о э ф ф и ц и е н т излучения между каждым из тел и поверхностью экрана:
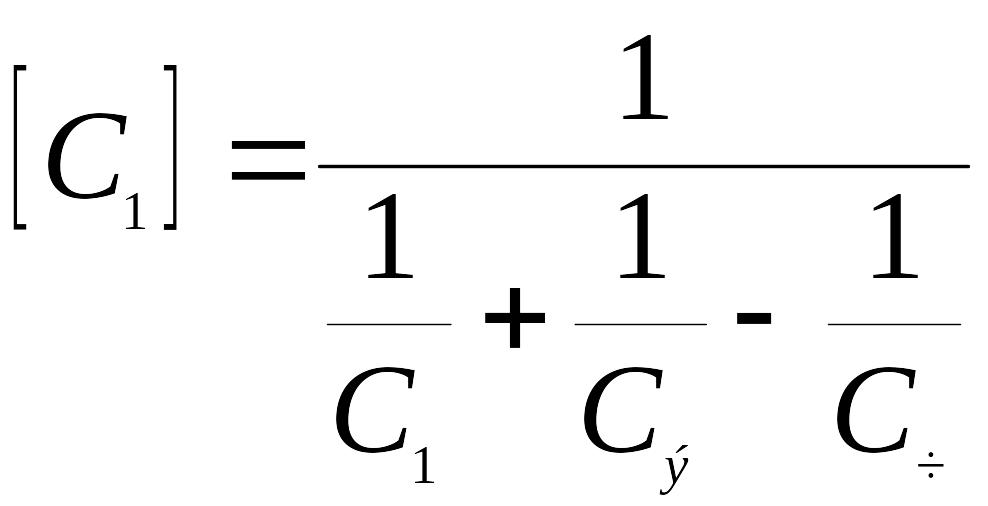
Величина q в формуле (24) представляет собой количество тепла на 1 мг, которым обмениваются тела I и II при отсутствии экранов.

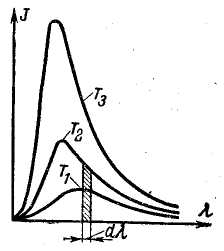
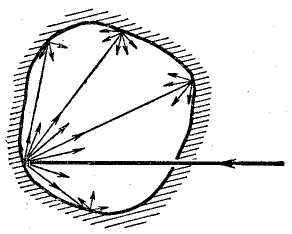
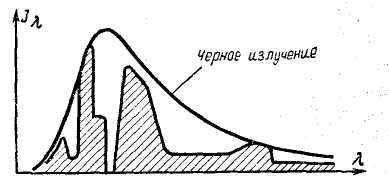
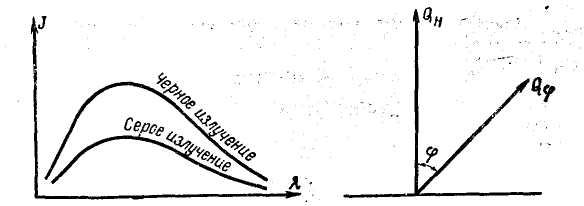

 Рис.
4. Спектр излучения серого
тела в сравнении со спектром
излучения черного тела.
Рис.
4. Спектр излучения серого
тела в сравнении со спектром
излучения черного тела.