3. Эмпирические формулы

В этом параграфе мы рассмотрим несколько типовых случаев теплообмена между твердой стенкой и движущейся жидкостью, имея в виду как капельные жидкости, так и газы; рассмотрены будут случаи движения вынужденного и свободного. Мы ограничимся наиболее важными в тепло­технике случаями продольного обтекания труб, при котором жидкость движется параллельно трубам, внутри них или между ними, и поперечного обтекания пучка труб, когда газ движется в направлении, перпендикулярном трубам. При этом будем рассматривать лишь турбулентное движение жидкости. Кроме того, мы остановимся на теплоотдаче при изменении агрегатного состояния.

1. Продольное обтекание труб. На основании теории подобия теплообмен при движении жидкости внутри труб характеризуется формулами типа (6-12) и (6-13). Много­численные опыты показали, что эти зависимости могут быть представлены степенным уравнением:

Nu = CRe^mPrⁿ (18)

где С, т и п - постоянные величины, определяемые по опытным данным.

Подробный анализ опытных данных приводит к следую­щей формуле ² для вычисления коэффициента теплоотдачи при турбулентном движении в гладких трубах:

(19)

Коэффициент А учитывает направление потока тепла, так как а зависит от того, происходит нагревание или охлаждение жидкости, и величину этого потока, причем для упругих жидкостей можно считать с достаточной сте­пенью точности А = 1. Для капельных жидкостей А = (Рr_ж/Рr_ст)^0,25 , где Рr_ж - критерий Прандтля при температуре жидкости, а Рr_ст - тот же критерий при температуре стенки. Эта температура при определении а еще неизвестна; однако так как указан­ное отношение входит в уравнение в степени 0,25, оно заметного влияния на а не оказывает и температурой стенки можно задаться приближенно.

Входящие в эти формулы величины выражены в едини­ системы МКС, а именно: а - вт/(м²•град); вт(м •град); - м!с; d - м; l - м С_р – дж/(кг•град); - н•сек/м²; - кг/м³.

Формула (19) справедлива для значений Re от 1 • 10⁴ до 5 • 10⁸ и Рr от 0,6 до 2500. Она дает среднее по всей длине трубы значение коэффициента теплоотдачи и относится к таким трубам, у которых l/d > 50. При отношении l/d < 50 следует вносить поправки, приводимые в спе­циальных курсах.

При пользовании формулой (19) особое внимание следует обращать на правильность выбора значений физи­ческих констант и др.), так как эти константы зависят от температуры. Как правило, надо брать значения физических констант для той температуры, которая при­нималась при выводе эмпирической формулы. Так, для фор­мулы (19) все физические константы надо относить к сред­ней температуре жидкости, а для которой вычисляется, т. е.

(20)

где t₁ - температура при входе в трубу;

t₂ - температура при выходе из трубы.

Формулой (19) можно приближенно пользоваться для вычисления коэффициента теплоотдачи и в тех случаях, когда газ движется внутри канала некруглого сечения. При этом канал произвольного сечения заменяется экви­валентной круглой трубой, диаметр d_экв которой опреде­ляется по формуле

(21)

здесь F - площадь поперечного сечения канала, по кото­рому течет газ;

U - периметр поперечного сечения (смоченный пери­метр, т. е. такой,

который определяет поверх­ность теплообмена).

Например, при движении газов в воздушном экономай­зере пластинчатого типа сечение потока имеет форму пря­моугольника. При сторонах прямоугольника а и b экви­валентный диаметр для этого случая будет:

(22)

а в случае, когда b велик по сравнению с а, просто

Рис. 5. Продольное внешнее обтекание труб.

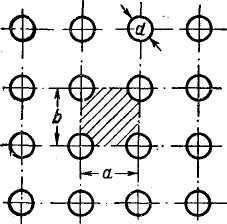
В теплотехнике часто рассматривается случай продоль­ного течения газа между трубами (рис. 5). В этом случае за сечение трубы можно при­нять заштрихованную на рисунке площадь, эквивалентный диа­метр для которой составляет:

(24)

Поперечное обтекание газом пучка круглых труб. Опыты по определению коэф­фициента теплоотдачи для этого важнейшего случая были по­ставлены рядом исследователей, и в первую очередь в советских научно-исследовательских институтах.

Если рассмотреть отдельную трубку, оказывается, что теплоотдача по ее окружности неодинакова; наибольшая теплоотдача наблюдается в ее лобовой и кормовой частях, наименьшая — по концам диаметра, перпендикуляр­ного направлению движе­ния жидкости. В пучке параллельных труб коэф­фициент теплоотдачи также неодинаков в разных точ­ках поверхности и для труб разных рядов. Для практических расчетов определяется среднее зна­чение по периметру всех труб пучка.

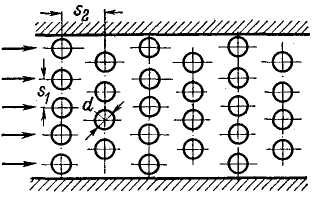
Как показывают данные исследований, коэффициент теплоотдачи в этом случае, помимо критериев Re и Рr, зависит от того, в каком порядке — коридорном (рис. 6) или шахматном (рис. 7) - расположены трубы.

Рис. 6. Поперечное обтекание газом пучка круглых труб (коридорное расположение).	Рис. 7. Поперечное обтекание газом пучка круглых труб (шахмат­ное расположение).

Многочисленные опыты, проведенные в ряде отечествен­ных институтов, привели к следующим расчетным формулам для любых жидкостей при значениях Re = 2 •10² 2 •10⁵;

при коридорном расположении труб в пучке

(25)

при ш а х м а т н о м расположении труб в пучке

(26)

Все физические кон­станты следует относить к средней температуре газа t_г, которая в первом приближении находится по формуле (6-20).

Скорость определяет­ся для наиболее узкого сечения между трубками одного поперечного ряда.

Формулы (25) и (26) дают среднее значение а для третьего и последую­щих рядов пучка. Чтобы найти а в первом пучке для обоих случаев расположения труб, нужно найденное значение а умножить на 0,6, для второго ряда — при коридорном расположении — на 0,9, при шах­матном — на 0,7; среднее значение а для всего пучка находится по следующей формуле:

(27)

где a_k и Н_k (поверхность нагрева) относятся к отдельному ряду труб.

Коэффициент теплоотдачи а зависит и от угла между направлениями потока газа и осей труб (угол атаки). Поправочный множитель в зависимости от угла атаки при­водится в специальных курсах; для 80 и 90° он равен 1; при углах от 70 до 10° он изменяется соответственно от 0,98 до 0,42.

Произведенные по формуле (25) расчеты показывают, что коэффициент теплоотдачи при шахматном расположе­нии труб выше, чем при коридорном; вместе с тем в этом случае больше и сопротивле­ние при движении газового потока.

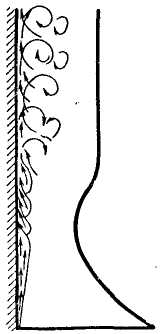
Теплоотдача при свободном дви­жении. Если около нагретой стенки (рис. 8) находится газ (или жидкость) и температура стенки отличается от температуры газа, то ближайшие к стенке части газа нагреются и как

более легкие поднимутся вверх, на их место подой­дет более холодный газ; в результате начнется циркуляция газа около стенки. Получающийся в этом случае тепло­обмен, при котором движение происхо­дит за счет разности удельных весов холодного и нагретого газа или жидкости, называется теплообменом при за свободном движении (естественной конвекции).

Рис. 8. Свободное движение газа около нагретой стенки.

Обработка многочисленных опытов, проведенных с различными жидкостями, движущимися около различных объектов (проволоки, трубы, плиты, шары и др.), привела к следующей формуле для вычисления а, при свободном движении газа и жидкости.

Nu = C(Gr•Pr)ⁿ. (28)

Значения С и п зависят от величины произведения Pr•Gr;

Здесь Gr - упомянутый выше критерий представляющий собой комплекс величин

Входящие в формулу величины с достаточной степенью точности могут быть взяты для среднеарифмети­ческой температуры жидкости и стенки:

(29)

где t_ж - принято по формуле (20).

Остальные величины, входящие в формулу (28):

g - ускорение силы тяжести;

- температурный напор, равный разности между температурой жидкости и стенки.

При пользовании формулой (28) необходимо иметь в виду, что для труб за линейный размер принимается диаметр d.

Теплоотдача при конденсации. Значи­тельно сложнее происходит процесс тепло­обмена в тех случаях, когда у поверхности стенки происходит изменение агрегатного состояния теплоносителя, как это имеет место при конденсации пара. В теплотехнике этот случай имеет большое значение, так как водяной пар — основное рабочее тело в теп­ловых двигателях, применяемых на электро­станциях и в промышленности.

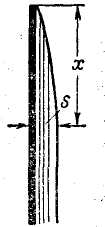
Процесс теплоотдачи при конденсации исследован Нуссельтом, который исходил из следующих представлений. Если (рис. 9) насыщенный пар при давлении р окружает трубу, температура стенки t_ст которой меньше температуры насыщения t_н пара, то вслед­ствие конденсации на поверхности трубы образуется пленка жидкости (так называемая пленочная конденса­ция), внешняя поверхность которой имеет темпера­туру t_н.

Рис. 9. Пленка кон­денсата на вертикаль­ной поверх­ности.

Пусть на расстоянии х от верхнего края трубы толщина слоя пленки равна s; исходя из предположения, что пленка стекает ламинарно, находим по закону Фурье плот­ность теплового потока через пленку:

где λ, - теплопроводность жидкости (конденсата).

С другой стороны, по определению коэффициента тепло­отдачи, q = a (t_н – t_cт). Сравнивая оба уравнения, полу­чаем: а = λ/s.

Как видно, коэффициент теплоотдачи прямо пропорцио­нален коэффициенту теплопроводности λ жидкости и об­ратно пропорционален толщине s пленки.

Массу конденсата М, получающуюся на единицу поверх­ности стенки трубы в единицу времени, получим, если q разделим на скрытую теплоту парообразования:

(30)

Для влажного пара вместо r следует подставить rх.

При теоретическом решении задачи Нуссельт вычислил толщину пленки s на высоте х и определил среднее значение коэффициента теплоотдачи.

Формула для толщины пленки имеет вид:

(31)

а средний коэффициент теплоотдачи для вертикальной стенки трубы

(32)

для горизонтальной

(33)

Величины относятся к средней температуре пленки

(34)

При пользовании формулами 30…32 все вели­чины, входящие в них, следует измерять в единицах какой-либо одной системы, в частности для СИ: Вт• м/(м² •град); р - кг/м³; r - дж/кг, - н•сек/м², а- вт/(м² • град).

Сравнение коэффициентов теплоотдачи, полученных опытным путем, с вычисленными по формулам (31) и (32) показывает, что последние на 20…22% менее факти­ческих. Это объясняют влиянием поверхностного натяже­ния, которое автором формул не было учтено.

Экспериментальные данные по теплоотдаче при конден­сации были обработаны в виде зависимостей между крите­риями подобия. Полученные формулы приводятся в спе­циальной литературе.

Из рассмотрения формул (32) и (33) видно, что, поскольку всегда H» d, коэффициент теплоотдачи при вертикальном расположении трубы меньше, чем при гори­зонтальном. Однако при большой высоте трубы пленка конденсата в нижней части начинает двигаться турбулентно. Средний коэффициент теплоотдачи перестает падать и даже несколько возрастает.

Для горизонтального пучка труб, как показывают но­вейшие исследования, влияние стекания конденсата с верх­них трубок на нижние может быть без большой ошибки учтено, если в формуле (33) вместо d поставить nd, где п - число рядов трубок по вертикали (для п ≤; 16).

При определении коэффициента теплоотдачи от перегре­того пара к стенке нужно различать два случая в зависи­мости от того, происходит ли конденсация пара на границе со стенкой или нет. Если температура стенки выше темпера­туры насыщения при давлении пара, то конденсация не происходит, и теплоотдача протекает так же, как у газов; коэффициент а в этом случае вычисляется по рассмотрен­ным выше формулам для продольного или поперечного обтекания. Если же температура стенки ниже температуры насыщения и на ней образуется конденсатная пленка, то коэффициент теплоотдачи а подсчитывается по формулам для конденсации насыщенного пара, причем за температуру пара принимается его температура насыщения, а вместо r подставляется значение і-і’, где і-энтальпия перегре­того пара, a і'- энтальпия кипящей жидкости того же давления (для не очень больших давлений).

Приведенные формулы (32) и (33) относятся к покоя­щемуся или слабодвижущемуся пару ( < 10 м/сек), лишен­ному примеси воздуха. Для больших скоростей пара при­меняются другие формулы, дающие большее а. При наличии воздуха в паре а резко уменьшается.

В технике чаще всего встречается пленочная кон­денсация.

В отдельных случаях, в частности при замасленной по­верхности стенки, наблюдается явление так называемой капельной конденсации, при которой вместо сплошной пленки стенка покрывается отдельными каплями воды, постепенно растущими, стекающими вниз и отрывающи­мися от стенки. При капельной конденсации коэффициент теплоотдачи резко возрастает и достигает 50000…100 000 вт/(м^2▪град)