5. Теплопередача через цилиндрическую стенку

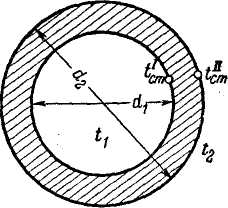
Расчетные формулы для теплообмена в случае цилин­дрической стенки составляются по тем же правилам, что и для плоской стенки; необходимо только знать термиче­ские сопротивления для тех же случаев распространения тепла, что и для плоской стенки.

Т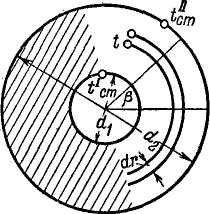 еплопроводность в твердом цилиндрическом теле. На рис. 6 изображено сечение цилиндрической стенки (тру­бы); пусть температура внутренней поверхности стенки равна , наружной , внутренний радиус r₁, наружный r₂.

Рис. 6. Тепловой поток через цилиндрическую стенку.

Существенное отличие распространения тепла в случае цилиндрической стенки от уже рассмотренного для плоской стенки заключается в том, что количество тепла, поступив­шее от находящейся внутри трубы среды на внутреннюю поверхность при распространении его к наружной, проходит через все увеличивающуюся поверхность и выходит к окру­жающей трубу среде через наружную поверхность, которая тем больше, чем больше наружный диаметр трубы. Для того чтобы иметь возможность и в рассматриваемом случае пользоваться уравнением Фурье, которое мы применили в случае плоской стенки, выделим внутри стенки цилиндри­ческие поверхности с бесконечно малой разностью радиусов dr. Тогда поверхности, через которые проходит поток тепла, можно будет принять одинаковыми и рассматривать стенку как плоскую. Разность температур dt между выделенными поверхностями будет также бесконечно малой. По уравнению Фурье [формула (1)], написанному для нашего случая, получаем:

При вычислении теплообмена в случае цилиндрических поверхностей принято вести расчет на поверхность трубы, соответствую­щую длине трубы в 1 м. Если обозначить через r радиус трубы в той части, где взят слой толщиной dr, то поверхность F трубы, соответствующая длине в 1 м, определится как боковая поверхность цилиндра высотой в 1 м и составит F - 2 . Количество тепла, отнесенное к единице длины трубы, называют линейным тепловым потоком (слово «линейный» часто опускают). Обозначим его q'. Тогда

откуда

Проинтегрируем это уравнение, приняв для t пределы и , что для r будет соответствовать пределам r₁ и r₂; тогда

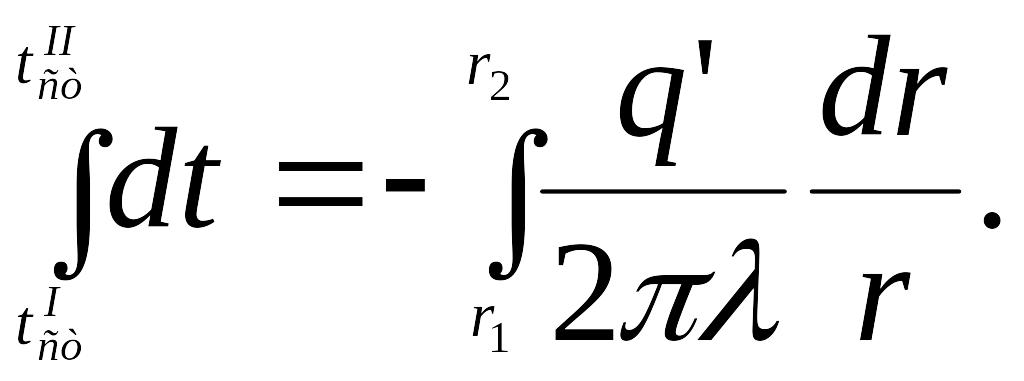
Вынося постоянные за знак интеграла и произведя интегрирование, получаем:

Умножим обе части равенства на -1 и вместо отношения радиусов примем равное ему отношение диаметров:

Отсюда получаем в обычном виде формулу теплового потока на 1 м длины трубы:

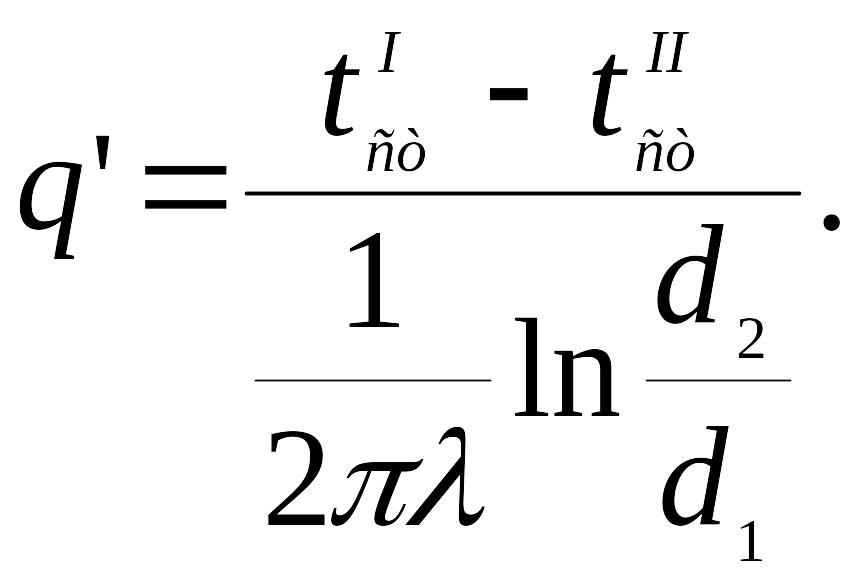(18)

Написанная в таком виде формула (18) показывает, что термическое сопротивление теплопроводности (отнесен­ное к единице длины трубы) в цилиндрической стенке имеет вид:

Если в это выражение поставить значение π и заменить натуральный логарифм десятичным, получим:

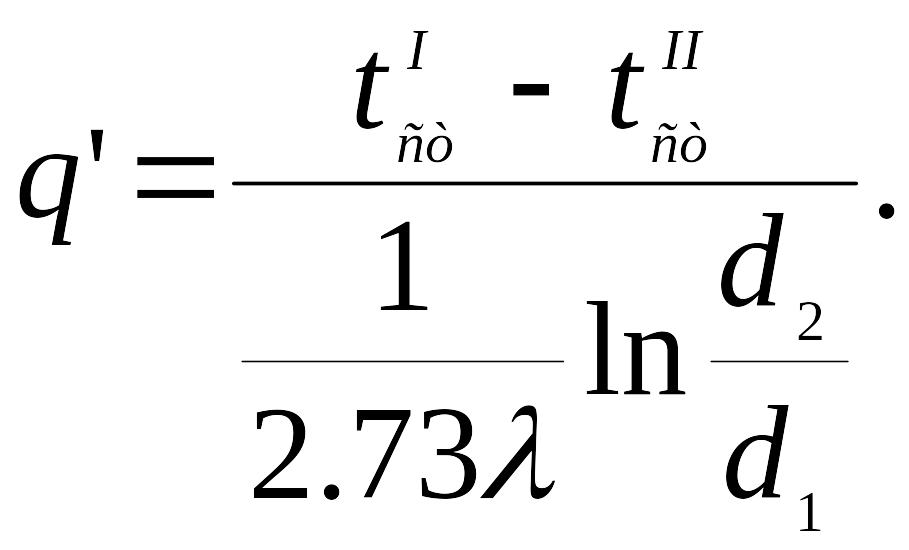(19)

Как и ранее, во всех формулах для теплового потока здесь в числителе - разность температур, в знаменателе - термическое сопротивление теплопроводности цилиндриче­ской стенки.

В случае многослойной цилиндрической стенки, поль­зуясь формулой 19), можно написать значение теплового потока для каждого слоя в отдельности и затем, вывести формулу для линейного теплового потока в случае сложной цилиндрической стенки. Она, например, для стенки из трех слоев будет иметь такой вид:

(20)

где d_1, d_2, d_3,, d₄ - диаметры цилиндрических поверхно­стей, ограничи-

вающих слои.

Теплоотдача к цилиндрической стенке. Пусть в трубо­проводе (рис. 7) протекает какая-либо жидкость, температура которой t_1, а температура внутренней поверхности стенки .

Рис. 7. Теплоотдача в случае цилиндрической стенки.

Количество тепла, которое пере­дается от жидкости к стенке (тепло­отдача), можно подсчитать по фор­муле (7).

Отнесем количество тепла к единице времени и к единице длины трубы. Площадь F составляет в этом случае боковую поверхность трубы высотой 1 м и определяется так:

Подставляя в основное уравнение получаем:

(21)

Придадим ей принятый ранее вид:

(22)

Если же нужно подсчитать теплоотдачу от наружной стенки трубы к окружающей ее жидкости, то аналогично формуле (22) можно написать:

где - температура наружной поверхности стенки;

t₂ - средняя температура жидкости, омывающей стенку;

d_г - наружный диаметр трубы.

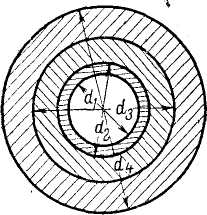
Теплопередача через цилиндрическую стенку. Если нуж­но подсчитать количество тепла, переданное от одной жидкости к другой через разделительную стенку (теплопе­редача), то формулу для этого случая можно написать по общему правилу, пользуясь уже известными выражениями для тер­мических сопротивлений. Возьмем самый общий случай, когда внутри и вне трубы протекают жидкости с температурами соответственно t₁ и t₂, для которых коэффициенты теплоотдачи составляют: от среды внутри трубы к внутренней по­верхности стенки а₁ и от внешней поверхности трубы к омывающей ее жидкости а₂; пусть раздели­тельная стенка состоит из трех слоев, диаметры поверхностей ко­торых d_1, d_2,, d_3,, d₄ (рис. 8).

Рис. 8. Теплопередача через многослойную цилиндрическую стенку.

Тогда поток определится выражением

(23)

Здесь в знаменателе первое и последнее слагаемые - термические сопротивления теплоотдачи между жидкостью и стенкой внутри и снаружи трубы, а остальные слагае­мые - термические сопротивления теплопроводности от­дельных слоев сложной стенки.

До сих пор рассматривались случаи, когда поток тепла направлен от жидкости, движущейся внутри трубы, к жид­кости, протекающей снаружи. Если поток тепла направлен в обратную сторону (снаружи внутрь), формула для потока тепла запишется по уже изложенному правилу. Если тем­пературу и коэффициент теплоотдачи для жидкости, омы­вающей наружную стенку трубы, обозначить соответст­венно t₁ и а_1, для жидкости, омывающей внутреннюю стенку трубы, t₂ и а₂, а внутренний и наружный диаметры обозначить, как и ранее, через d₁ и d_2,, то формула для теплового потока через однослойную стенку примет вид:

Если нужно вычислить значение температуры для какой-либо промежуточной поверхности, то можно приме­нить ранее полученное правило. Так, температура определится формулой (для случая на рис. 8)

(24)

или

(25)

Коэффициент теплопередачи определится как отноше­ние количества переданного тепла к величине той или дру­гой поверхности и к разности температур.

Для расчета теплопередачи через тонкие трубы (в кон­денсаторах, котлах, подогревателях), имеющие отношение d₂/d₁, близкое к единице, можно пользоваться формулами для плоской стенки.