Содержательный модуль 3 «теплопередача» лекция 7. Основные случаи теплообмена. Теплопроводность (4) план

1. ОПРЕДЕЛЕНИЯ

2. ТЕПЛОПРОВОДНОСТЬ В ТВЕРДОМ ТЕЛЕ. РАСПРОСТРА-НЕНИЕ ТЕПЛА В ОДНОСЛОЙНОЙ И МНОГОСЛОЙНОЙ ПЛОСКОЙ СТЕНКЕ

3. ТЕПЛООТДАЧА МЕЖДУ СТЕНКОЙ И ЖИДКОСТЬЮ

4. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ПЛОСКУЮ СТЕНКУ

5. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ЦИЛИНДРИЧЕСКУЮ СТЕНКУ

1. Определения

Если тело А передало каким-либо образом телу В некоторое количество тепла Q, то говорят, что между этими телами произошел теплообмен.

Различают два принципиально отличных друг от друга вида теплообмена. Один из них связан с преобразованием энергии: это—теплообмен излучением, или радиацией. В этом случае тепловая энергия, теряемая телом А, превра­щается в лучистую энергию; распространяющиеся лучи достигают тела В, и здесь происходит полное или частич­ное преобразование лучистой энергии в тепловую, которая и воспринимается телом В.

Другой вид теплообмена заключается в том, что передача тепла от одного тела к другому происходит путем соприкос­новения.

В теплотехнике особенно важен теплообмен соприкос­новением между движущейся жидкостью и твердым телом, получивший название теплоотдачи. Этот вид теплообмена встречается в тепловых аппаратах как часть общего случая перехода тепла от одной жидкости к другой через разде­ляющую их стенку. Такой общий случай мы будем назы­вать теплопередачей. Под жидкостью мы в данном случае разумеем как к а п е л ь н у ю жидкость, так и у п р у г у ю жидкость - газ.

В качестве примера рассмотрим явление теплообмена в паровом котле. Тепло от дымовых газов передается как соприкосновением, так и излучением металлу трубок и от них — воде, движущейся внутри трубок. В этом случае переход тепла в отдельности от газов к стенкам трубок и от стенок трубок к воде мы будем называть теплоотдачей, комплексное же явление перехода тепла от газов к воде - теплопередачей.

Как видно, два способа теплообмена - радиацией и соприкосновением — могут происходить одновременно.

Теплообмен между двумя какими-либо телами связан с распространением тепла внутри одного и того же тела как твердого, так и жидкого.

Распространение тепла в н у т р и одного и того же тела может быть двоякого рода. В одном случае тепло внутри тела может распространяться теплопроводностью (кондукцией); при этом отсутствует движение конечных масс тела; сущность же переноса тепла заключается в том, что вслед­ствие наличия разности температур молекулы тела в той его части, где температура выше, обладают большей кине­тической энергией и при столкновениях с соседними моле­кулами передают им часть своей энергии. Так осуществ­ляется перенос тепловой энергии.

Сущность теплообмена соприкосновением, связанного с распространением тепла теплопроводностью, впервые с кинетической точки зрения правильно объяснил М. В. Ло­моносов в своем труде «Размышления о причине теплоты и стужи». При этом он исходил из закона сохранения движе­ния, что видно из следующих его слов: «Если более теплое тело А приходит в соприкосновение с другим телом В, менее теплым, то находящиеся в соприкосновении частички тела А быстрее вращаются, чем частички тела В. От более быстрого вращения частички тела А ускоряют вращатель­ное движение частичек тела В, т. е. передают им часть своего движения; сколько движения уходит от первых, столько же прибавляется ко вторым. Поэтому, когда час­тички тела А ускоряют вращательное движение частичек тела В, то замедляют свое собственное, а отсюда, когда тело А при соприкосновении нагревает тело В, то само оно охлаж­дается».

В жидкостях наряду с теплопроводностью тепло может распространяться и благодаря перемешиванию нагретых и не нагретых слоев жидкости, при котором и происходит перенос тепла. Такой вид распространения тепла назы вается распространением тепла конвекцией или просто конвекцией. Очевидно, что в твердых телах не может идти речь о переносе тепла этим способом.

Распространение тепла конвекцией связано, таким обра­зом, с движением самой жидкости, части которой, переходя в область с другой температурой, обмениваются теплом с соседними частями.

Следует иметь в виду, что тепло в жидкостях может пере­даваться и исключительно теплопроводностью. Так, если нагрев неподвижной жидкости, находящейся в сосуде, производить сверху, то никакой конвекции не происходит и тепло будет передаваться лишь молекулярным процессом, т. е. теплопроводностью. Однако количество тепла, пере­даваемое теплопроводностью, при наличии конвекции в боль­шинстве случаев играет относительно малую роль.

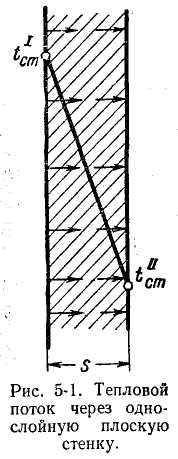
2. ТЕПЛОПРОВОДНОСТЬ В ТВЕРДОМ ТЕЛЕ. РАСПРОСТРАНЕНИЕ ТЕПЛА В ОДНОСЛОЙНОЙ И МНОГОСЛОЙНОЙ ПЛОСКОЙ СТЕНКЕ

Мы рассмотрим здесь случай распространения тепла в однородном твердом теле, когда весь поток тепла, подво­димый к поверхности стенки, имеющей температуру (рис. 1), проходит через тело и уходит наружу через противоположную поверхность стенки, температура кото­рой равна .

Если с течением времени температура в каждой точке внутри стенки не меняется, то такой поток тепла назы­вается стационарным, или установившимся.

Если поток тепла нестационарный, то часть под­водимого тепла идет на нагревание самой стенки (или происходит ее охлаждение), и в этом случае темпера­тура в каждой точке внутри тела с течением времени меняется.

Обычно на практике установлению стационарного потока предшествует нестационарный режим, при котором стенка нагревается (или охлаждается). Когда это нагревание пре­кращается, нестационарный режим переходит в стационар­ный.

По эмпирическому закону Фурье количество тепла, проходящее в твердом теле от одной поверхности стенки с температурой к другой с температурой , прямо пропорционально поверхности стенки, разности температур и времени, обратно пропорционально толщине стенки и, наконец, указанное количество тепла зависит от свойств материала, из которого сделана стенка.

Если обозначить: Q - количество тепла, которое про­ходит от одной поверхности стенки к другой; - темпе­ратура одной поверхности стенки, °С; - температура другой поверхности стенки, °С; τ - время; s - толщина стенки; F - поверх­ности стенки, то

(1)

Для бесконечно-тонкой стенки с толщиной ds уравнение (5-1) принимает вид:

Знак минус поставлен потому, что по смыслу дифференциала dt - здесь число отрицательное, так как темпера­тура по направлению потока тепла умень­шается.

Дробь представляет собой изменение температуры на единицу пути потока, называется градиентом темпе­ратуры.

Для того чтобы установить смысл коэффициента пропорциональности λ, надо решить уравнение относительно него и всем величинам, кроме Q, входящим в полученное значение λ, придать значение единицы. Получаем:

Следовательно, коэффициент λ измеряет количество тепла, распространяющееся в течение 1 с. в теле от одной его поверхности размером в 1 м² к другой такой же поверх­ности при толщине тела 1 м и при разности температур на поверхности 1⁰. Этот коэффициент называется коэффи­циентом теплопроводности или просто теплопроводностью тела и измеряется в системе МКС единицей дж • м/(м² • с • град), а так как Дж/с = Вт, то единицей измерения служит величина Вт - м/(м² • град).

Опыт показывает, что коэффициент теплопроводности зависит от температуры, и при точных расчетах эта зависи­мость должна учитываться.

Количество тепла Q, отнесенное к единице времени и измеряемое в дж/сек (вт) или ккал/ч, называют тепловым потоком (иногда тепловой мощностью); тепловой поток, отнесенный к единице поверхности и измеряемый в Вт/м² или ккал/(м² • ч), называют поверхностной плотностью теплового потока или кратко - плотностью теплового по­тока (обозначают q).

Таким образом, если разделить обе части уравнения (1) на Fτ, получим:

(2)

Часто уравнение (2) записывают в таком виде:

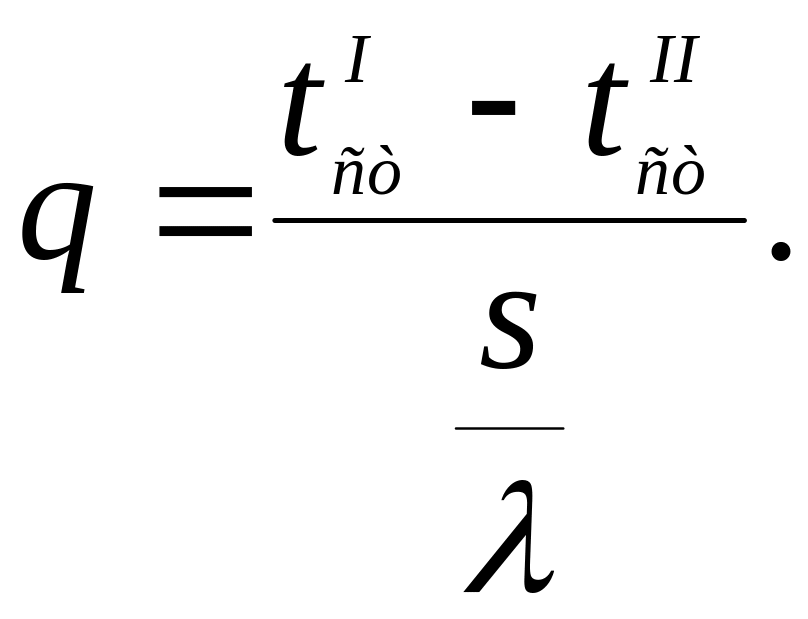(3)

В этом виде формула для теплового потока может быть уподоблена формуле закона Ома для постоянного тока, и тогда плотность теплового потока q в формуле (5-3) соот­ветствует плотности электрического тока, проходящего через единицу площади сечения проводника в формуле закона Ома, а разность температур — разности потенциа­лов, величина s/λ - омическому сопротивлению, приходя­щемуся на единицу сечения в той же формуле. В соответст­вии с этим величина s/λ называется термическим сопротив­лением теплопроводности.

Таким образом, для данного случая можно установить следующее правило: плотность теплового потока численно равна частному от деления разности температур поверхно­стей стенки на термическое сопротивление теплопровод­ности между этими поверхностями, В дальнейшем это пра­вило будет распространено и на явления теплоотдачи и теплопередачи.

Важной характеристикой материалов служит величина называемая коэффициентом температуропроводности, еди­ницей ее измерения служит в системе МКС величина м²/с.

Р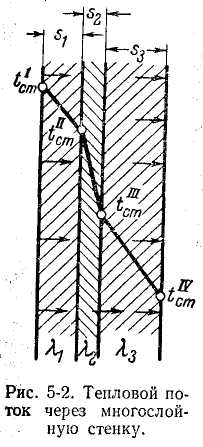 ассмотрим плоскую стенку, составленную из несколь­ких - положим, трех - отдельных слоев. Пусть темпера­туры на границах слоев, толщины стенок и значения коэф­фициентов теплопроводности для каждой из стенок будут такими, как это указано на рис. 2. Тепловой поток, проходящий через каждую из стенок, будет по величине один и тот же, поскольку мы рассматриваем стационарный режим. Отсюда для каждой из стенок на основании уравнения (3) можно написать:

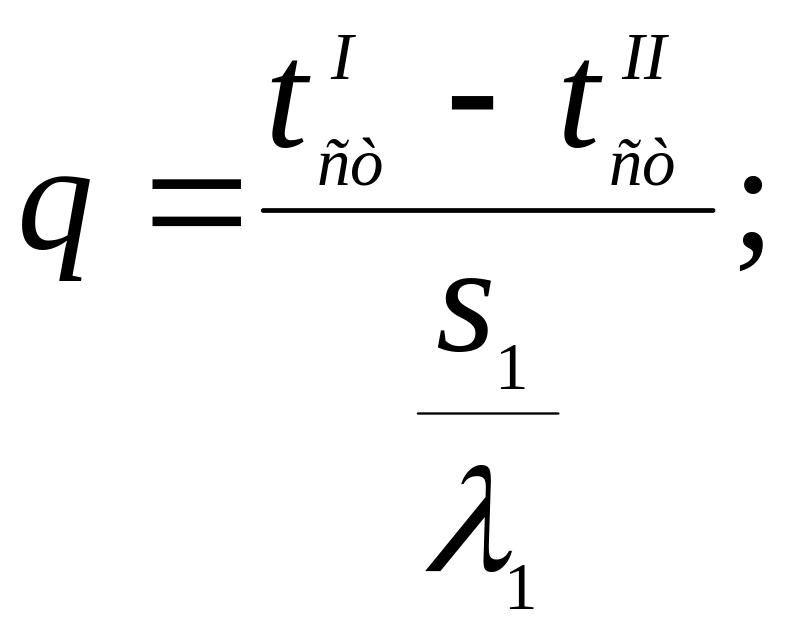
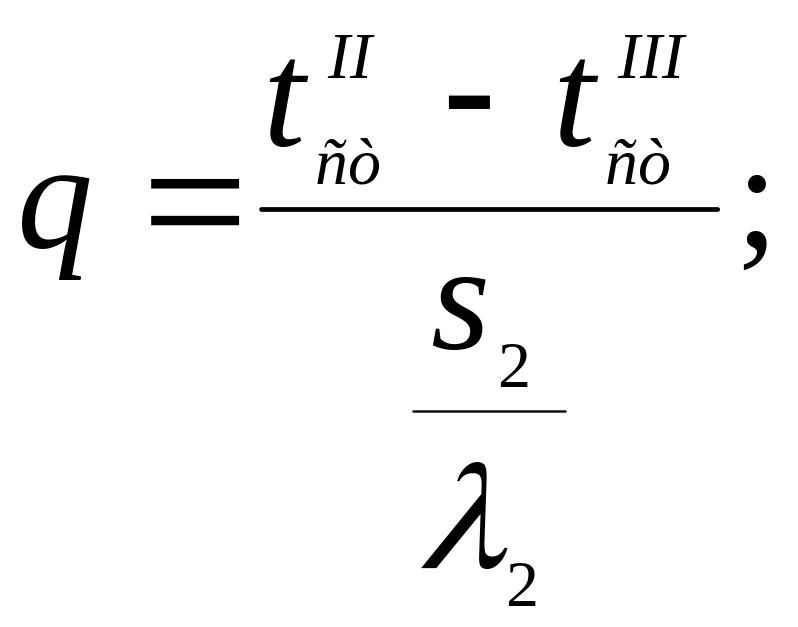
Из написанных уравнений можно получить:

(а)

Складывая почленно все уравнения, получим:

Отсюда 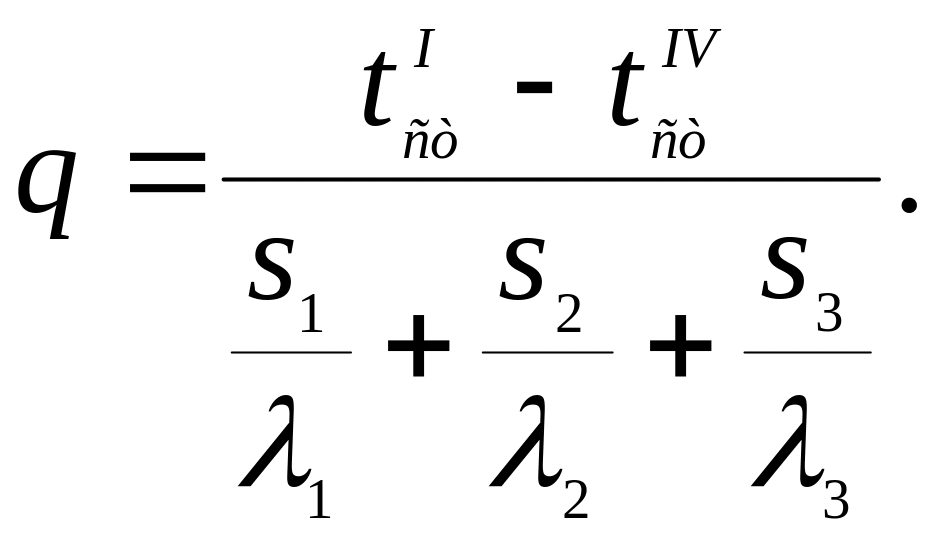(4)

Если полученную формулу сравнить с формулой (3), можно заключить, что формула (4) составлена по тому же правилу: в числителе стоит разность температур граничных поверхностей, а в знаменателе - термическое сопротивле­ние между рассматриваемыми граничными поверхностями, которое в данном случае представляет собой сумму терми­ческих сопротивлений отдельных слоев.

Анализируя уравнения (а), можно составить правило для вычисления какой-либо из промежуточных температур; так из второго уравнения находим:

из третьего уравнения можно написать:

Полученные уравнения позволяют установить сле­дующее правило. Температура данной изотермической поверхности тела (т. е. такой поверхности, во всех точках которой температура одинакова), например , равна температуре какой-либо предыдущей изотермической по­верхности, в этом случае , за вычетом произведения теплового потока q на термическое сопротивление s₃/λ₃ между рассматриваемыми поверхностями; или температура данной изотермической поверхности, например , равна температуре какой-либо последующей поверхности, сложенной с произведением теплового потока q на терми­ческое сопротивление s₃/λ₃ между рассматриваемыми по­верхностями.

Так, если желательно вычислить температуру t_x в точке, отстоящей на расстоянии х (рис. 2) от крайней правой поверхности третьего слоя, по температуре t¹, то на осно­вании выведенного правила получим:

(5)

или по температуре

(6)

Зависимость (6) при λ = const - уравнение прямой линии, так что температура в любой точке по толщине стенки изменяется пропорционально расстоянию точки от рассматриваемой граничной поверхности, что и видно на рис. 2.

Изложенные здесь два правила - одно для вычисления теплового потока, другое для вычисления температуры - будут в дальнейшем нами использованы для других случаев теплообмена.