- •Моделювання системи магнітний підсилювач (тиристорний збудник-генератор-дпс) на основі системи з загальним суматором
- •Моделювання системи дпс при реверсуванні
- •Моделювання системи двозонного керування тп-дпс
- •Моделювання систем непрямого регулювання швидкості
- •Моделювання системи з паралельним коригуванням
- •Лінійна модель системи трн-ад
- •Моделювання системи трн-ад при використанні лінійної моделі ад
- •Моделювання системи трн-ад у фазних координатах
- •Моделювання системи пч-ад при підтримці законів частотного регулювання
- •Моделювання системи пч-ад в ортогональній системі координат
- •Дослідження систем електропривода на стійкість та якість
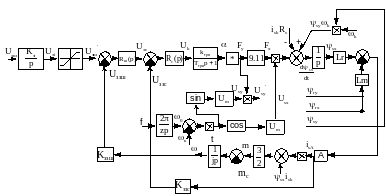
Моделювання системи з паралельним коригуванням
Система з паралельним коригуванням представляє собою систему ГД з загальним суматором та трьома зворотними зв’язками по напрузі генератора, струму та швидкості двигуна. Обмотка збудження генератора живиться від регульованого тиристорного перетворювача. Зворотній зв'язок по напрузі генератора будується з врахуванням падіння напруги на активному опорі генератора. Зворотній зв'язок по струму реалізований у вигляді струмової відсічки тобто він працює при перевищенні струмом двигуна значення струмової відсічки.
Побудуємо математичну модель
. (6.1)
Перейдемо у простір Лапласа:
. (6.2)
Виражаємо струм%
, (6.3)
. (6.4)
Стала часу:
. (6.5)
ЕРС:
, (6.6)
, (6.7)
. (6.8)
Нехтуємо падінням напруги на активному опорі генератора.
, (6.9)
, (6.10)
, (6.11)
, (6.12)
, (6.13)
, (6.14)
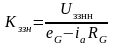 , (6.15)
, (6.15)
 , (6.16)
, (6.16)
, (6.17)
 . (6.18)
. (6.18)
Коефіцієнт
зворотного зв’язку як при рівнозначних
зворотних зв’язках без урахування
спаду напруги
 .
.
Побудуємо структурну схему:

Лінійна модель системи трн-ад
Лінеаризація системи ТРН-АД полягає в тому, що момент АД змінюється лінійно відносно напруги. Це є грубим припущенням, оскільки відомо що момент двигуна пропорційний квадрату напруги. Таким чином квадратичну залежність моменту двигуна від напруги представляють прямою лінією, яка проходить через точку (0;0) і точку номінального режиму роботи

 . (7.1)
. (7.1)
Розглянемо систему ТРН-АД з двома контурами зворотного зв’язку по струму і швидкості обертання. Побудуємо функціональну схему:

Основне рівняння руху:
, (7.2)
 , (7.3)
, (7.3)
Побудуємо мат модель системи
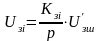 , (7.4)
, (7.4)
, (7.5)
 , (7.6)
, (7.6)
 , (7.7)
, (7.7)
В лінеаризованій системі ТРН-АД струм Ад можна прийняти пропорційним моменту, тому зворотній зв'язок по струму реалізуємо по моменту
 , (7.8)
, (7.8)
. (7.9)
Система (7.1) – (7.9) є математичною моделлю лінеаризованої моделі ТРН-АД

Моделювання системи трн-ад при використанні лінійної моделі ад
Для моделювання скористаємось лінійною моделлю АД.
Лінійна модель АД.
 , (8.1)
, (8.1)
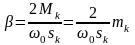 , (8.2)
, (8.2)
, (8.3)
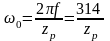 . (8.4)
. (8.4)
Рівняння (8.1)–(8.4) – лінійна модель.
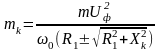 , (8.5)
, (8.5)
 , (8.6)
, (8.6)
 , (8.7)
, (8.7)
 , (8.8)
, (8.8)
, (8.9)
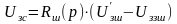 , (8.10)
, (8.10)
, (8.11)
, (8.12)
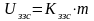 , (8.13)
, (8.13)
. (8.14)
Система рівнянь (8.1)-(8.14) – математична модель системи ТРН-АД при використанні лінеарезованої моделі АД.
Недоліки цієї моделі:
Неможливаість виконання реверсу двигуна;
Неможливість використання моделі при ковзанні двигуна від sкр до 1.
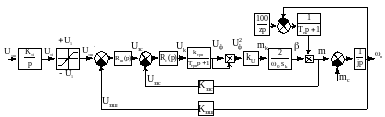
Моделювання системи трн-ад у фазних координатах
Для моделювання використаємо фазну модель АД в ортогональній системі координат х-у.
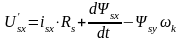 , (9.1)
, (9.1)
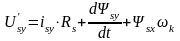 , (9.2)
, (9.2)
 , (9.3)
, (9.3)
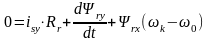 , (9.4)
, (9.4)
 , (9.5)
, (9.5)
 . (9.6)
. (9.6)
(9.1)-(9.6) – фазна система.
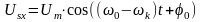 , (9.7)
, (9.7)
 , (9.8)
, (9.8)
Враховуючи дискретний характер роботи тиристорів напруга записана в (9.7) та (9.8) буде прикладатися до двигуна в момент часу коли тиристор відкритий, коли тиристор закритій це U=0.
Один із способів моделювання дискретного характеру роботи є використання перемикаючих функцій. Ці функції можуть приймати значення 1 або 0.
Тому (9.1)-(9.8) доповнимо наступними рівняннями:
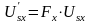 , (9.9)
, (9.9)
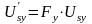 , (9.10)
, (9.10)
Перемикаючі функції Fx та Fy залежать від кута відкривання тиристорів альфа, при чому вони повинні повторювати одна одну з відставанням на 90 градусів. Тому можна записати що
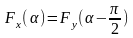 , (9.11)
, (9.11)
Система керування ТРН представлено періодичною ланкою І-того порядку.
 , (9.12)
, (9.12)
Припустимо електропривод має два зворотні зв’язки по струму статора та швидкості обертання.
, (9.13)
, (9.14)
, (9.15)
, (9.16)
, (9.17)
 . (9.18)
. (9.18)
Для моделювання АД у фазних координатах система рівнянь (9.1)–(9.6) потрібно представити залежно від струму або потокощеплення. Розглянемо випадок, коли вона представляється відносно потокощеплення.
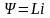 :
:
 , (9.19)
, (9.19)
 , (9.20)
, (9.20)
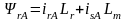 , (9.21)
, (9.21)
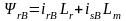 , (9.22)
, (9.22)
 , (9.23)
, (9.23)
 , (9.24)
, (9.24)
Підставимо (9.24) у (9.24) – отримаємо:
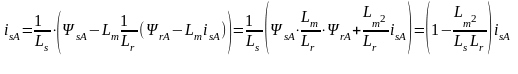
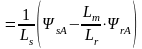 , (9.25)
, (9.25)
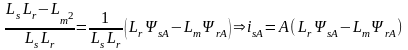 , (9.26)
, (9.26)
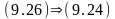

 . (9.27)
. (9.27)
Аналогічним
чином знайдемо
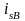 ,
, .(9.28),(9.29)
.(9.28),(9.29)
Система рівнянь (9.12)-(9.29) е математичною моделлю в ортогональній системі координат ху.
На основі математичної моделі побудуємо структурну схему:
* - логічні умови що записують графіки перемикаючих функцій;