3.21 Основы расчета рамных конструкций переменного сечения из сварных двутавров с гибкой стенкой

Скляров И.А. (КНУСА, г. Киев, Украина)

Статья посвящена исследованию напряженно-деформированного состояния рамных конструкций из сварных двутавров переменного сечения с гибкой стенкой. Учет закритической работы гибкой пластины после потери устойчивости позволяет значительно снизить металлоемкость каркасов за счет использования внутреннего ресурса несущей способности.

Abstract. Article is devoted to the research of stress-strain state of the welded frame structure with variable double-T cross section with a flexible wall. Accounting for supercritical work of the flexible plate after buckling can significantly reduce the metal consumption of the skeletons through the use of bearing capacity internal resources.

Повышение уровня традиционных критериев эффективности двутав-ровых профилей может быть проще всего достигнуто за счет повышения тонкостенности сечения, а именно – увеличения гибкости стенки. Анализ критериев эффективности сечений показывает, что при постоянном значении площади сечения двутавра эффективным является тот профиль, который имеет более тонкую стенку, так как это дает возможность без увеличения площади сечения принять двутавр с большей высотой и получить повышение соотношения момента сопротивления к единице площади. Однако требования строительных норм по проектированию стальных конструкций ограничивают гибкость стенки, что приводит к существенному росту материалоемкости конструкций.

Цель исследований – повышение уровня эффективности применения рациональных стальных каркасов из сварных двутавров переменного сечения путем исследования характера работы составного сечения с гибкой стенкой после местной потери устойчивости.

Расчет тонкостенных рамных конструкций ставит перед инженером несколько достаточно сложных задач. Во-первых, сложно прогнозировать нелинейную поведение конструкции после местной потери устойчивости стен-ки сечения. Кроме того, исключение из работы стенки при сжатии вызывает перераспределение внутренних напряжений и развитие упруго-пластических деформаций в полках сечения. Не упрощает эту задачу также наличие начальных несовершенств стенки, которых при малой толщине и значительной гибкости почти невозможно избежать. В строгой математической форме решение является настолько трудоемким, что не может применяться рядовыми проектировщиками.

Единственным рациональным путем формализации методики расчета рамных конструкций из двутавров с гибкой стенкой является проведение экспериментальных испытаний и разработка полуэмпирических формул для их расчета.

Начало систематических исследований поведения пластин после потери устойчивости было положено работами ученых А. Феппля, Т. Кармана и И. Г. Бубнова [1, 2, 3].

В конце 30-х годов, опираясь на расчеты Вагнера [4], А.Ю. Ромашевский [5] в ЦАГИ выполняет исследования и проводит испытания моделей балок с очень гибкими стенками из алюминиевого сплава с ребрами жесткости, расположенными на расстоянии, равном половине высоты балки, и гибкостью стенок от 1200 до 2000. На основе этих исследований была разработана методика расчета таких балок.

Последующие экспериментальные исследования показали, что такой подход дает удовлетворительные результаты только для балок с очень жесткими поясами и ребрами, которые имеют значительную гибкость стенок. Так П. Куном [6] на основе большого количества экспериментальных испытаний балок с гибкой стенкой и использования предыдущих исследований Вагнера, Стригунова и др. разработана методика их расчета. Интересным в его работах является то, что напряжение сдвига он предлагает делить на напряжение сдвига от диагонального поля растяжения и на напряжение от чистого сдвига.

Наибольшую известность из-за своей наглядности получил метод расчета балок с гибкой стенкой, предложенный американскими исследователями К. Баслером и Б. Тюрлиманом [7]. В основе их метода лежит построение условной статически допустимой модели предельного состояния при одновременной действия изгиба и сдвига. Кроме того, авторы исследуют вопрос зависимости устойчивости пояса от гибкости стенки и приходят к выводу, что предельная гибкость стенки, при которой пояс до достижения в нем напряжений, равных пределу текучести, не теряет устойчивости в вертикальной плоскости, равна 360.

В дальнейшем модель Баслера-Тюрлимана подвергалась уточнению и дополнению теоретико-экспериментальными исследованиями ученых Фуджии, Рокки, Шкалоуда, Броуде, Моисеева, Предтеченского, Погодаева, Каленова, Корчака, Дюбека, Ааре, Лепика, Евстратова и др.

Проведенные учеными исследования конструкций с гибкой стенкой касаются преимущественно балок. Работы же в отношении тонкостенных рамных элементов носят чисто теоретический характер и требуют экспериментальных подтверждений. Исследования относительно конструкций переменного сечения с гибкой стенкой автору в литературе не встречались.

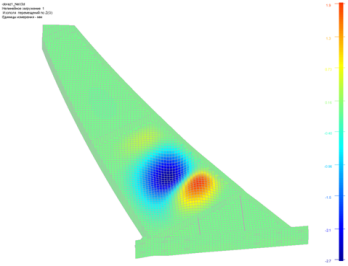
Большинство современных практиков в области проектирования стальных конструкций [8, 9] рекомендуют рассчитывать рамные элементы по той же методике, что и балочные конструкции с гибкой стенкой. Такой подход оправдан при значениях относительного эксцентриситета m_ef=(M/N)(A/W)>20. При меньших же значений m_ef напряженно-деформированное состояние элементов рамных каркасов несколько меняется – из-за влияния сжимающего усилия и возникают дополнительные внутренние напряжения. В закритической стадии работы стенки в полках сечения возникают местные изгибающие моменты [10]. Изгибающий момент в сжатой полке возникает вследствие деформаций стенки и «проседания» полки, которая работает как балка на упругом основании с переменными коэффициентами постели (в зависимости от характера деформирования стенки – рисунок 1).

а)	б)
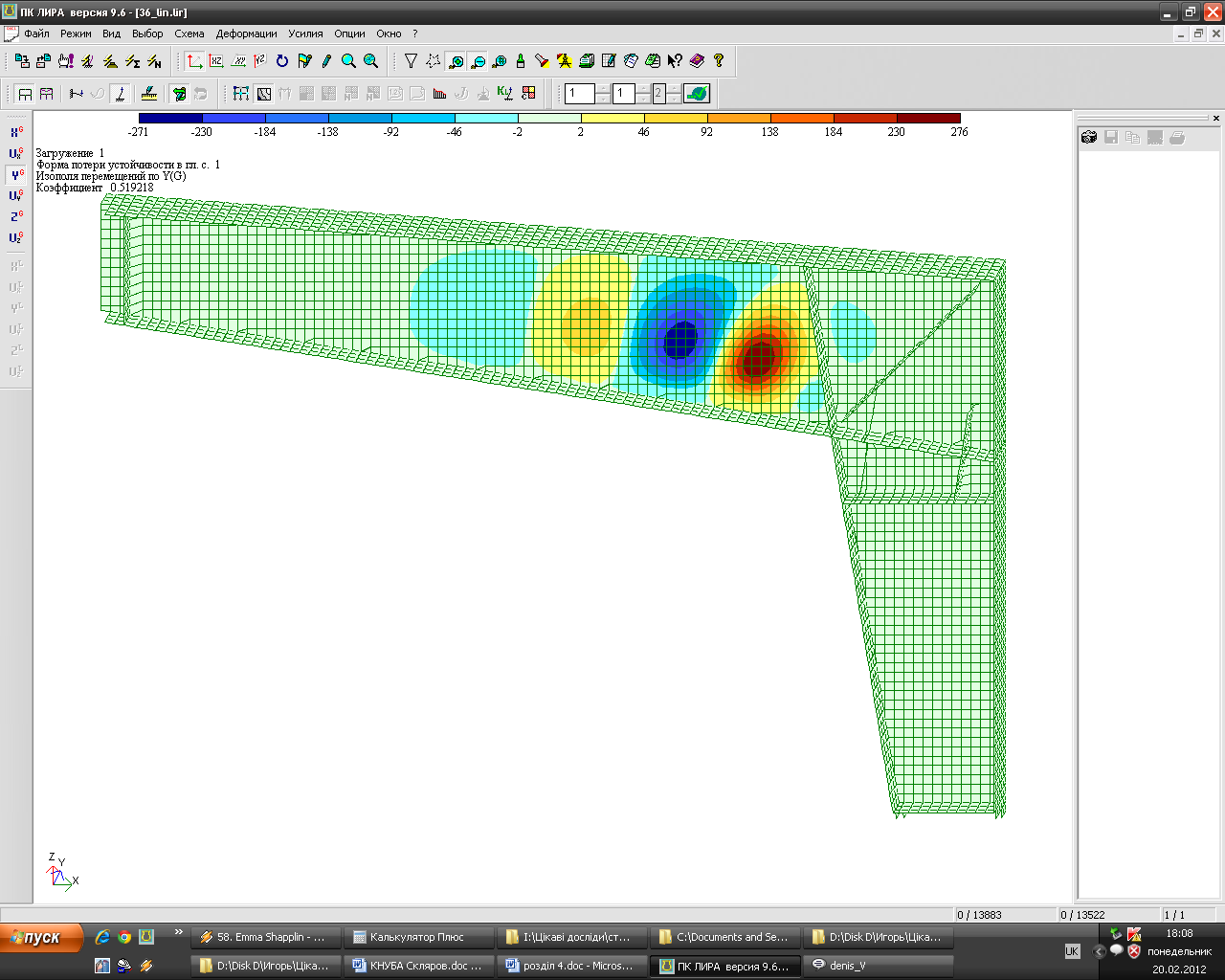
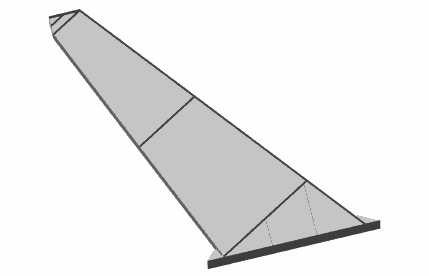
Рисунок 1- Напряженно-деформированное состояние рамного элемента переменной жесткости с гибкой стенкой в среде программного комплекса Лира по результатам линейного (а) и нелинейного (б) расчета

Рисунок 2 - Аналитическая модель экспериментального образца и общий вид установки при испытании

Для исследования работы рам из сварных двутавров переменного сече-ния с гибкой стенкой на кафедре металлических и деревянных конструкций Киевского национального университета строительства и архитектуры были проведены экспериментальные исследования элементов рам (рисунок 2).

В результате проведения ряда экспериментов установлено, что работа тонкостенных двутавровых рамных элементов принципиально отличается от работы элементов с устойчивыми стенками. В конструкциях из тонкостенных двутавров, вследствие повышенной деформативности стенки и ее неизбежных начальных несовершенств, боковое деформирование начиналось почти сразу с приложением внешней нагрузки. С увеличением нагрузки боковые прогибы стенки приобретали характерный вид, что определялось напряженным состоянием отдельных участков.

Характер потери устойчивости стенки вполне совпадает с результатом численных исследований – форма деформирования соответствует 1-й форме потери устойчивости по результатам численного эксперимента в программном комплексе Лира 9.6. Максимальные деформации стенки из плоскости наблюдались в сжатой зоне сечения.

Начальные прогибы стенки определяют направления бокового деформи-рования. Несмотря на значительные прогибы стенок при нагрузке, которые достигали 4-5 t_w, работа рамных элементов в целом имела упругий характер вплоть до предельных нагрузок. Остаточные деформации в стенке после снятия нагрузки не превышали ее толщины.

С учетом возникновения догружающих моментов в сжатой полке сечения, максимальные напряжения в тонкостенном рамном элементе следует определять по формуле (1):

,

(1)

где N, M – сжимающее усилие и изгибающий момент от действия внешней загрузки; A_red, W_red – площадь и момент сопротивления ослабленного двутаврового сечения с гибкой стенкой; M_fс – дополнительный изгибающий момент, который возникает в поясе после потери устойчивости стенки; I_fc – момент инерции таврового сечения, образованного сжатой полкой и частью стенки высотой h_wred; y₀ – расстояние от центра тяжести таврового сечения сжатого пояса до грани пояса; k_c – коэффициент, учитывающий перераспределение догружающего изгибающего момента и зависящий от гибкости стенки:

k_c =1 для сечений, у которых ;

для сечений, у которых .

Анализ результатов показал непригодность существующих методик для расчета рамных элементов с гибкой стенкой. Различие теоретических и экспериментальных результатов по существующим методикам составляет до 30%, в то время как по формуле 1 разница составляет менее 3%.

Разработаны две расчетные модели сечения для определения несущей способности сжато-изогнутого двутавра с гибкой стенкой. В первой центральная часть стенки исключается из работы и принимается расчетное редуцированное несимметричное сечение (рисунок 3, а). Такая расчетная схема сечения образуется при применении стенки с условной гибкостью =8-12. В случае, когда значение условной гибкости снижается до 6-8, жесткость стенки несколько больше, поэтому она способна воспринимать нагрузку также и в закритической стадии (рисунок 3,б). Поэтому при втором подходе предполагаем, что часть стенки после потери устойчивости частично воспринимает изгибающий момент, поперечную силу и продольное усилие. Сечение принимают несимметричным после потери устойчивости стенки.

Уменьшение жесткости стенки во второй методике предлагается определять умножением ее толщины на редукционный коэффициент, который зависит от значения условной гибкости стенки:

t_wred=ηt_w; , где – условная гибкость стенки, – экспериментальная верхняя граница условной гибкости стенки, при которой полка двутавра не теряет устойчивости в вертикальной плоскости.

а)	б)
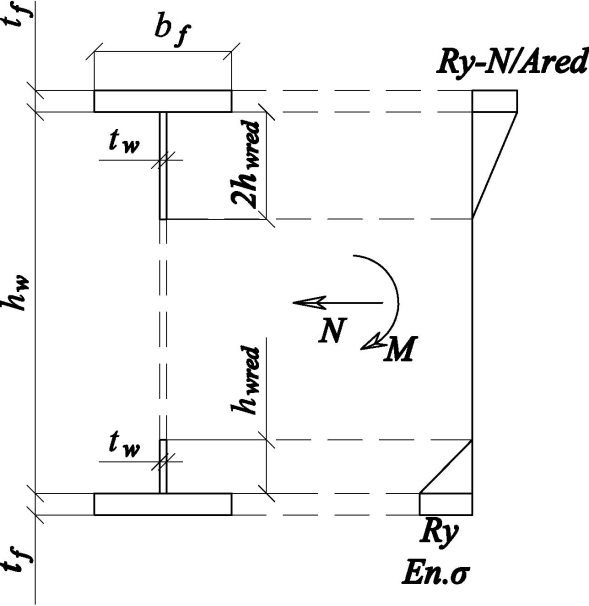
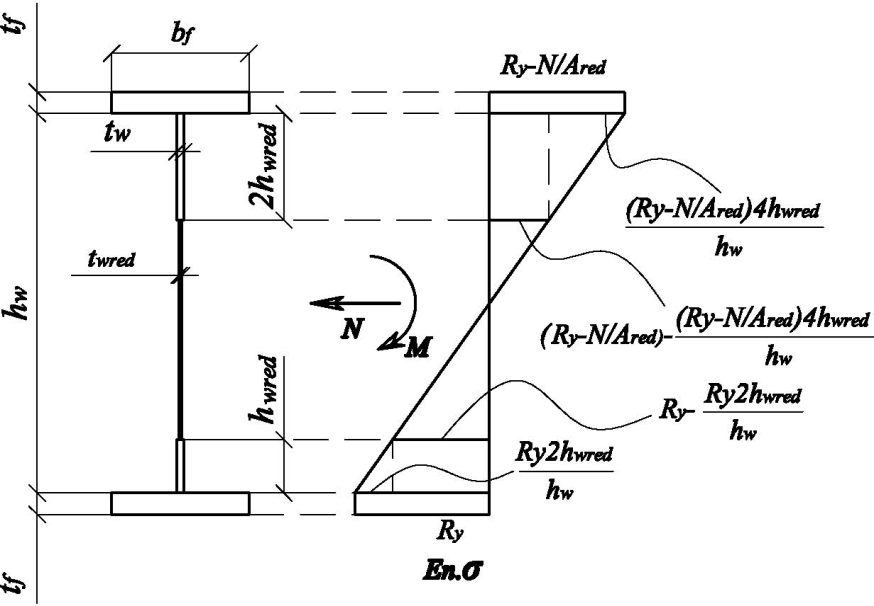
Рисунок 3 - Расчетное сечение рамы с гибкой стенкой без учета работы стенки (а) и при учете редуцированной толщины стенки (б). Эпюра нормальных напряжений в сечении

При совместном действии в сечении продольного, поперечного усилия и изгибающего момента несущую способность элементов из двутавров с гибкой стенкой следует определять по формуле (2):

(2)

В формуле (2) N, M_x, Q – усилия, действующие в сечении; N_и, M_иφ, Q_и – соответствующие предельные значения усилий.

Предельное значение изгибающего момента:

, где W_xred – момент сопротивления ослабленного сечения, зависящий от выбранного типа расчетной модели сечения; R_y – расчетное сопротивление стали; α=N/(A_redR_y) – коэффициент использования сечения по сжимающему усилию. Предельное значение сжимающей силы:

, где А_red – площадь ослабленного сечения, зависящая от выбранного типа расчетной модели сечения; φ – коэффициент продольного изгиба рассматриваемого элемента рамы.

Коэффициент условий работы γ_с, учитывая сложную работу элементов переменной жесткости с гибкой стенкой, рекомендуется ограничить значением 0,95. Предельное значение поперечного усилия Q_u допустимо определять по соответствующим формулам СНиП как для балки с гибкой стенкой.

Заключение

Увеличение гибкости стенки в двутавровых рамных каркасах является логичным и эволюционным путем совершенствования конструкций сплошного сечения. Но работа таких систем имеет сложный характер – нелинейное деформирование гибкой пластины, которая теряет устойчивость уже на начальных стадиях загрузки, а также одновременное действие сжимающего усилия, изгибающих моментов и поперечных сил в сечении требуют пересмотра существующих методик расчета тонкостенных двутавров. На основе собственных численных и экспериментальных исследований разработана методика проверки несущей способности рамных каркасов с гибкой стенкой.

Литература

[1]. Феппль А. Сила и деформация: прикладная теория упругости. Т. 2 / А. Феппль, Л. Феппль – М.-Л. : Главная редакция общетехнической литературы и номографии, 1938. – 408 с.

[2]. Karman. Th. The strength of thin plates in compression / Th. Karman, E. E. Sechler, L. H. Donnell // Transaction of the ASME. Vol. 54 – New York : ASME, 1932. – P. 53-57.

[3]. Бубнов И. Г. Труды по теории пластин / Бубнов И. Г. – М. : Гостехиздат, 1953. – 423 с.

[4]. Вагнер Г.В. Балки с весьма тонкой стенкой / Г.В. Вагнер // Сборник переводов ЦАГИ / под редакцией Уманского А.А. и Знаменского П.М. – М. : ЦАГИ, 1937. – С. 58-117.

[5]. Ромашевский А.Ю. Исследование работы балочных систем с тонкой стенкой с параллельными поясами / А.Ю. Ромашевский // Труды ЦАГИ. Вып. 206. – М. : 1935. – С. 5-53.

[6]. Кун П. Расчет на прочность оболочек в самолетостроении / Кун. П. – М. : Оборонгиз, 1961. – 306 c.

[7]. Basler К. Strength of plate girders in bending / К. Basler, В. Thurlimann // Proc. of American Society of Civil Engineers. Vol. 87, №. ST 6 – 1961. – P. 153-181.

[8]. Трофимов В.И. Легкие металлические конструкции зданий и сооружений (разработка конструкций, исследования, расчет, изготовление, монтаж) / В.И. Трофимов, А.М. Каминский / Учебное пособие. – М.: Изд–во АСВ, 2002. – 576 с.

[9]. Катюшин В.В. Здание с каркасами из стальных рам переменного сечения / В.В. Катюшин. – М.: Стройиздат , 2005. – 651 с.

[10]. Скляров І. О., Білик С.І. Експериментальні дослідження тонкостінних рамних двотаврів / Збірник наукових праць «Ресурсоекономні матеріали, конструкції, будівлі та споруди». – Випуск 24. – Рівне, 2012. – С. 248-254.