3.20 Конечно-элементное моделирование деформаций железобетонных плит

Серпик И.Н., Швачко С.Н., Муймаров К.В. (БГИТА, г. Брянск, РФ)

Разрабатывается процедура конечно-элементного анализа железобетонных плит при дискретном учете арматурных стержней. Получение возможности эффективных решений с помощью предлагаемого алгоритма рассматривается на примере расчета прямоугольной железобетонной плиты, шарнирно опертой по двум противоположным кромкам.

The finite element procedure for analysis of reinforced concrete plates with the discrete representation of armature is developed. The possibility of getting the effective solutions by using the proposed algorithm is considered on the example of calculation of a rectangular reinforced concrete plate simply supported on two opposite edges.

Вопросы расчета железобетонных плит с учетом физически нелинейной работы деформируемых систем и возможности образования трещин в растянутом бетоне рассматривались в работах [1, 2]. Алгоритм решения задач такого типа реализован в программном комплексе STARK_ES [3]. При этом учитываются приведенные характеристики железобетона как однородного анизотропного материала. Данный подход к анализу работы железобетонных плит не позволяет выполнять эффективного исследования поведения конструкций при нерегулярном расположении арматуры.

В настоящей работе представляется итерационный алгоритм расчета железобетонных плит методом конечных элементов с учетом дискретности армирования. В целом для плиты считается справедливой гипотеза прямых нормалей. Принимаются основные положения моделирования деформаций бетона с трещинами и без трещин Н.И. Карпенко [4]. Вводится система тонких слоев бетона, каждый из которых находится в условиях плоского напряженного состояния (рисунок 1). Арматура представляется в виде стержней, испытывающих только деформации растяжения или сжатия. При описании перемещений в бетоне используется схема аппроксимации перемещений, предложенная в работе [5]. Стержни арматуры разбиваются на ферменные конечные элементы.

На первом этапе выполняется расчет объекта в линейной постановке с учетом начальных модулей упругости материалов. Далее осуществляется итерационный процесс метода переменных параметров упругости. В каждой итерации при формировании матриц жесткости конечных элементов бетона и арматуры переопределяются матрицы упругости на основании напряжений, полученных на предыдущей итерации. Для бетона с этой целью в точках интегрирования конечных элементов оценивается уровень нагруженности материала [4] по каждому из слоев. Уровень нагруженности позволяет пересчитать механические характеристики бетона при отсутствии трещин, оценить характер трещинообразования при появлении условий разрушения в растянутом бетоне, проверить бетон на отсутствие раздробления при сжатии.

Рисунок 1 – Модель плиты: 1 – слои бетона; 2 – стержни арматуры

В разработанном алгоритме первоначально в направлении , перпендикулярном каждой трещине, модуль упругости бетона задается равным нулю, и на этой основе вычисляются матрицы упругости конечных элементов в локальных и глобальных осях. Далее приближенно учитывается условие работы бетона между трещинами. При этом связанная с глобальными осями матрица упругости конечного элемента слоя бетона, получаемая в итерации k, вычисляется для каждой точки интегрирования на основе зависимости

,

где – матрица упругости в глобальных осях Oxy, сформированная без учета нормальных напряжений в направлениях ; , , – нормальные напряжения по осям Ox, Oy и касательное напряжение в этой системе осей, соответствующие осредненным нормальным напряжениям в направлениям осей для итерации k-1; , , – относительные продольные деформация и сдвиговая деформация для данной системы осей, полученные в итерации k-1.

Рассматриваемая вычислительная схема реализована в программном комплексе DIVLOC, разработанном на кафедре механики БГИТА.

Пример расчета плиты.

С целью верификации разработанного алгоритма выполнялся расчет железобетонной плиты (рисунок 2), рассмотренной в работе [3]. Плита свободно оперта по коротким сторонам и подвержена действую постоянной равномерно распределенная нагрузки интенсивностью q. Рассматривается бетон класса В25 и арматура класса А-II. С учетом продолжительного действия нагрузки в этой задаче для бетона принимается: начальный модуль упругости ; нормативные сопротивления при сжатии и растяжении ; коэффициент Пуассона . Для арматуры задается: площадь поперечного сечения каждого стержня ; модуль упругости материала ; нормативное сопротивление .

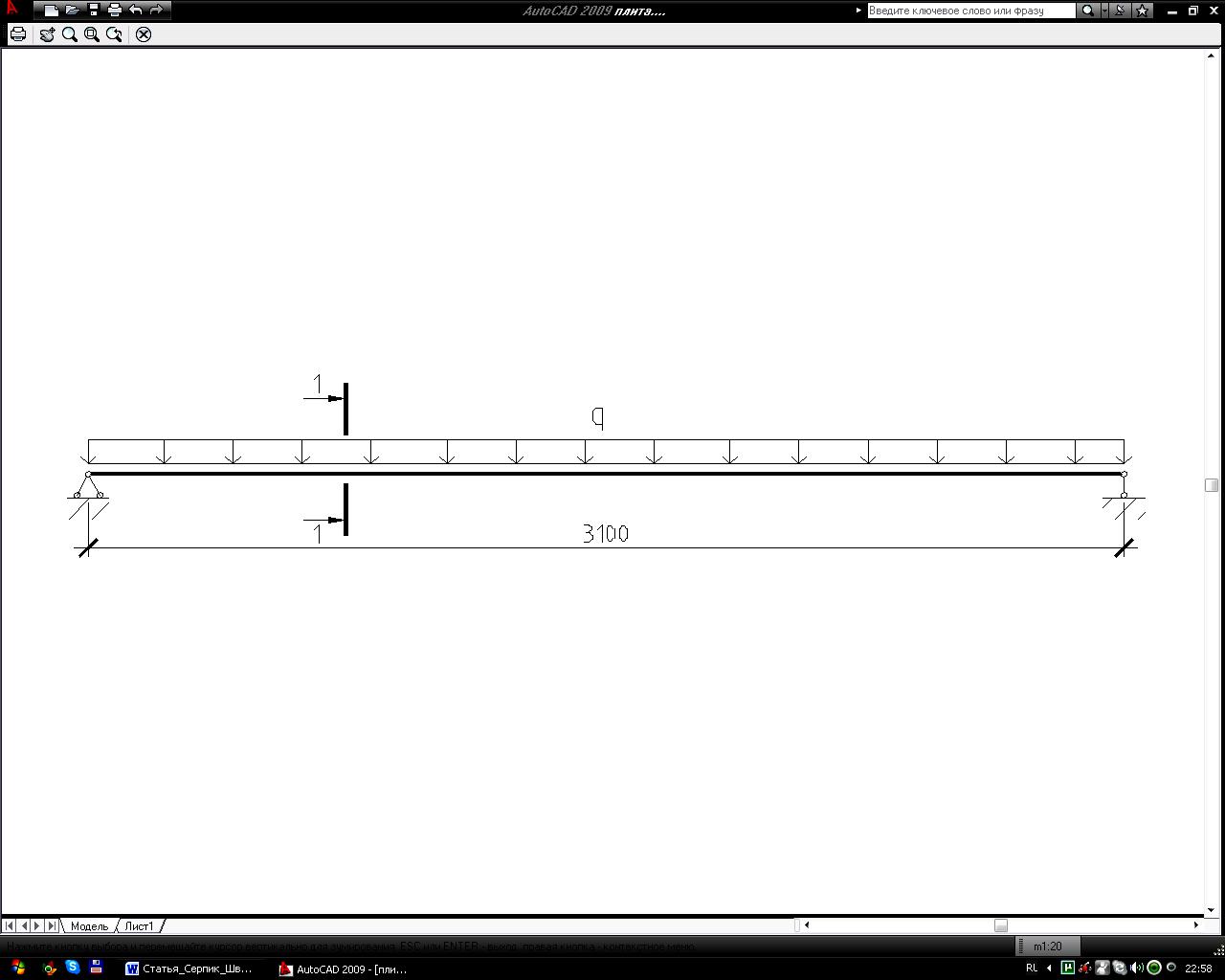
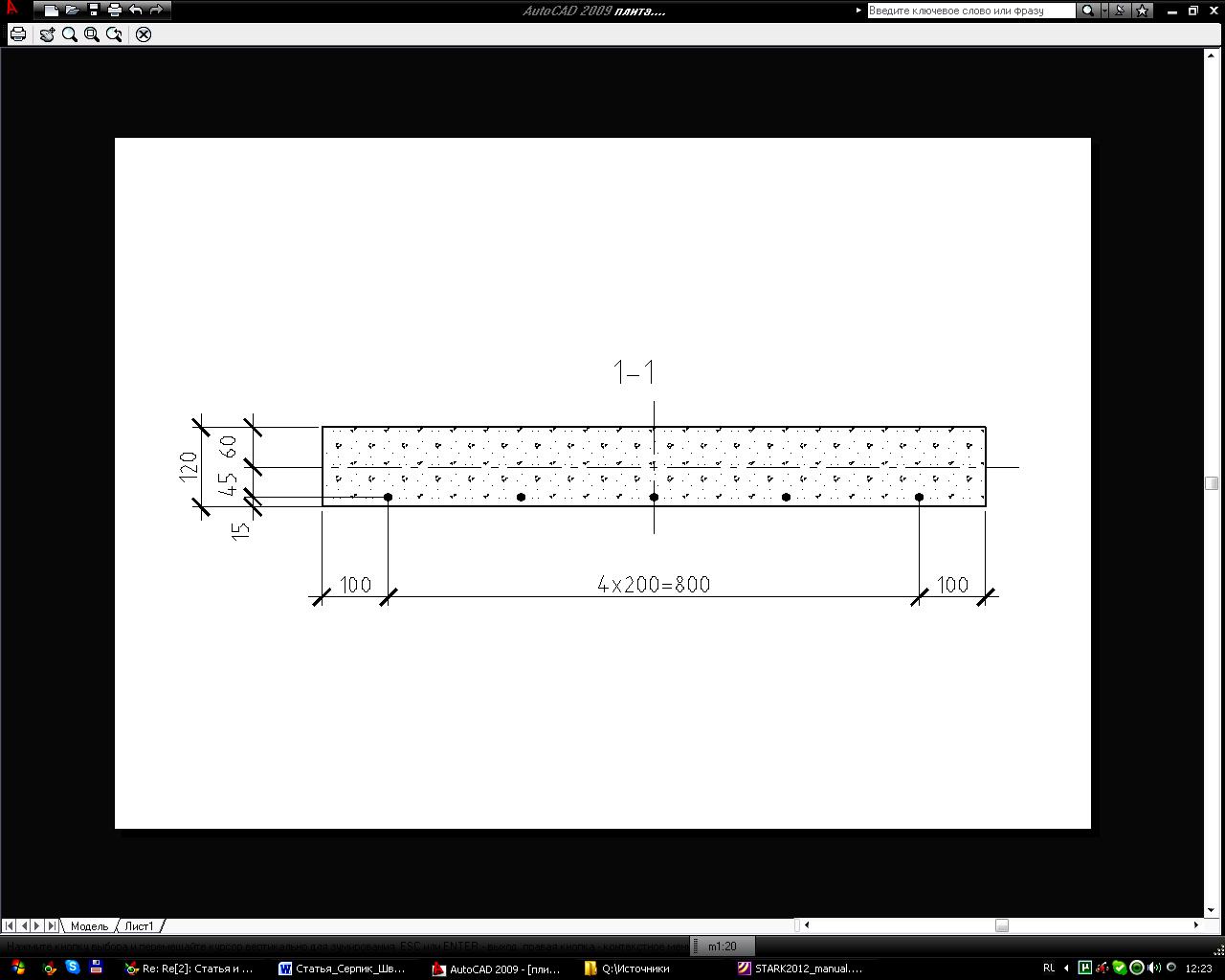
Рисунок 2 – Схема опирания, нагружения и поперечное сечение плиты

Рисунок 3 – Разбивка плиты на конечные элементы (КЭ)

Рисунок 4 – Сравнение максимальных прогибов плиты

При расчете использовались 120 треугольных слоистых конечных элементов бетона и 104 стержневых конечных элементов арматуры (рисунок 3). Рассматривалось несколько значений интенсивности нагружения. Практическая сходимость итерационного процесса решения нелинейной задачи достигалась за 5-15 итераций. Фиксировалось образование трещин в растянутом бетоне для 4 кПа. При этом в стержнях арматуры напряжения для рассматриваемых нагрузок не превышали значения .

Заключение

Предложена итерационная схема расчета железобетонных плит методом конечных элементов с учетом работы бетона между трещинами. Достаточно высокая точность разработанной методики подтверждена на основе решения тестовой задачи для прямоугольной плиты.

Литература

1. Клованич, С.Ф. Продавливание железобетонных плит. Натурный и численный эксперименты [Текст]/ С.Ф. Клованич, В.И. Шеховцов. – Одесса: ОНМУ, 2011. – 120 с.

2. Палювина, С.Н. Совершенствование расчета прочности и трещиностойкости железобетонных плит на основе численных методов : автореф. дис. канд. техн. наук [Текст] / С.Н. Палювина. – Белгород; 2000. – 28 с.

3. STARK_ES 2012. Руководство пользователя [Текст]. – М.: Еврософт, 2012. –339 с.

4. Карпенко, Н.И. Общие модели механики железобетона [Текст] / Н.И. Карпенко. – М.: Стройиздат, 1996. – 416 с.

5. Serpik, I.N. Development of a new finite element for plate and shell analysis by application of generalized approach to patch test [Text] / I.N. Serpik // Finite Elements in Analysis & Design. – 2010. – Vol. 46, N. 11. – P. 1017-1030.