3.14 Свободные колебания упругих ортотропных пластинок в виде правильных многоугольнков с однородными граничными условиями

Савин С.Ю. (Госуниверситет–УНПК, г. Орел, РФ)

В статье рассматриваются задачи о свободных колебаниях упругих ортотропных пластинок в виде правильных многоугольников с однородными граничными условиями. Построены аппроксимирующие функции, которые могут быть использованы непосредственно для нахождения значений основных частот колебаний пластинок в виде правильных многоугольников либо для получения опорных значений при решении задач о свободных колебаниях ортотропных пластинок произвольного очертания методом интерполяции по коэффициенту формы.

The article describes the problem of free oscillations of elastic orthotropic polygonal plates with homogeneous boundary conditions. It constructed approximating functions that can be used to find the values of the fundamental frequencies of oscillations polygonal plates directly or obtain as reference for solving problems of free vibrations of orthotropic plates of arbitrary shape by interpolation technique by shape factor.

Одним из эффективных методов расчета пластинок различного очертания в плане является метод интерполяции по коэффициенту формы [1], который позволяет свести решение дифференциальных уравнений эллиптического типа в задачах строительной механики пластинок к решению геометрической задачи на основе установленного в работе [2] подобия между коэффициентом формы и интегральными геометрическими характеристиками пластинок. Для эффективного применения этого метода к решению задач о свободных колебаниях в ненагруженном состоянии упругих ортотропных пластинок, существует потребность в построении граничных кривых для значений этой интегральной характеристики, необходимых для применения МИКФ.

В настоящей работе выполняется построение граничных кривых для значений основной частоты колебаний в ненагруженном состоянии упругих ортотропных пластинок в виде правильных многоугольников с однородными граничными условиями.

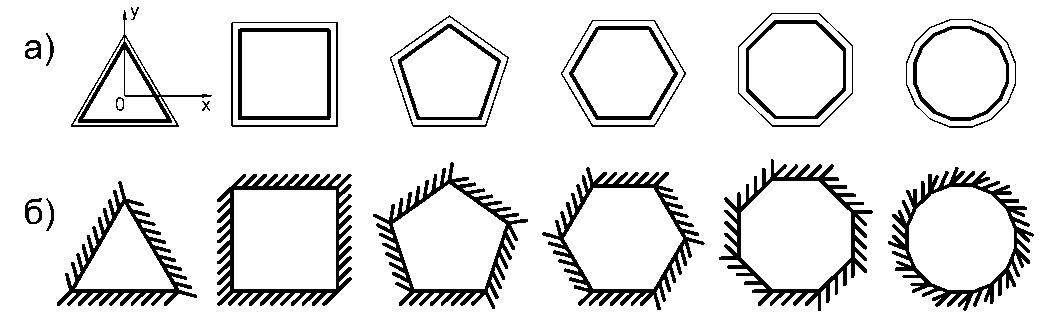
Рисунок 1 – Пластинки в виде правильных многоугольников, одна из осей ортотропии которых

направлена параллельно стороне: а) шарнирно опертые по контуру, б) жестко защемленные

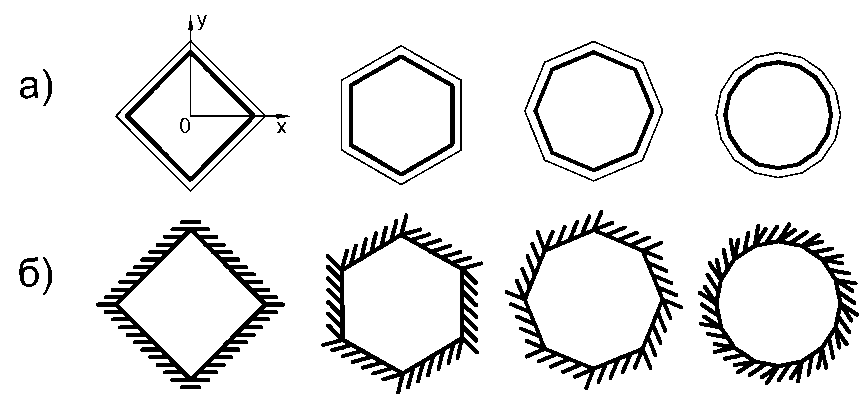
Рисунок 2 – Пластинки в виде правильных многоугольников, оси ортотропии которых проходят

через вершины: а) шарнирно опертые по контуру, б) жестко защемленные

Для правильных многоугольников можно выделить два основных варианта направления осей ортотропии: одна из осей ортотропии направлена вдоль стороны многоугольника (рисунок 1); оси ортотропии проходят через вершины многоугольника (рисунок 2). Построение граничных функций осуществлялось путем обработки результатов численных расчетов по МКЭ, выполненных в программном комплексе SCAD, пластинок с определенным очертанием формы области при соотношениях цилиндрических жесткостей D_x /H = 1, 2 … 5; D_y /H = 1, 2 … 5.

Каждая пластинка разбивалась не менее чем на 500 конечных элементов. Выбор такой густоты разбиения пластинок на конечные элементы обусловлен следующим обстоятельством: для пластинок решались тестовые задачи при разной густоте разбиения на конечные элементы (250, 500, 1000). При увеличении числа конечных элементов, приходящихся на одну пластинку, начиная с 500, значения основных частот колебаний практически совпадали.

Ввиду большого количества полученных данных, результаты расчета по МКЭ в настоящей работе не приводятся. Ограничимся тем, что сразу приведем значения коэффициентов в полиномах, являющихся граничными функциями для поиска опорных решений при использовании методики МИКФ.

Построение граничных функций

Для свободных колебаний ортотропной пластинки из теории упругости известно следующее дифференциальное уравнение:

, (1)

где

В этих выражениях D_x, D_y, D_xy – цилиндрические жесткости пластинки, ν_x, ν_y – коэффициенты Пуассона по соответствующим направлениям, m – масса пластинки, приходящаяся на единицу её площади. Разделим правую и левую части уравнения (5) на H:

, (2)

где – собственное значение дифференциального уравнения. В этом случае при прочих одинаковых условиях (форма пластинки, собственное значение β⁴, граничные условия и цилиндрическая жесткость H) решение будет зависеть от двух параметров уравнения:

В изопериметрическом виде выражение для определения основной частоты собственных колебаний изотропных пластинок, формы областей которых могут быть объединены некоторым геометрическим преобразованием, представляется зависимостью [1]:

(3)

где – коэффициент формы, – некоторая функция, зависящая от граничных условий, постоянная для пластинок с формой области одного класса (треугольные, трапециевидные и т.д.).

Однако для ортотропных пластинок функция K_ω будет также зависеть и от соотношения цилиндрических жесткостей и Осуществим замену соотношения на функцию . С учетом этого выражение (3) для ортотропных пластинок примет вид:

(4)

Неизвестную функцию g из выражения (4) будем искать следующим образом. По значениям максимальных прогибов, используя программный комплекс Table Curve 3D, построим аппроксимирующие функции , где n – число сторон пластинки в виде правильного многоугольника:

. (5)

Таблица 1 – Значения коэффициентов A … E в выражениях (6) и (7)

К-ты A …F (6)	Одна из осей ортотропии направлена вдоль стороны многоугольника
	Коэффициенты a … j выражения (5)
	a	b	c	d	e	f	g	h	i	j
Шарнирное опирание (рисунок 1, а)
A	-6448	4459	1987	-1438	-466,1	-2,786	145,7	32,58	26,53	-13,59
B	3356	-2302	-1051	742,6	251,5	-13,97	-75,21	-17,75	-13,25	8,349
C	-648,7	442,8	207,1	-142,8	-50,39	5,563	14,45	3,588	2,457	-1,849
D	55,23	-37,51	-17,93	12,09	4,433	-0,7074	-1,223	-0,3182	-0,2005	0,1764
E	-1,743	1,179	0,5751	-0,3799	-0,1441	0,0292	0,0384	0,0104	0,0061	-0,0061
Жесткое защемление (риснок 1, б)
A	875,6	-364,1	-224,2	-202,8	-181,2	329,3	20,29	19,48	-16,89	-6,004
B	-461,1	204,0	130,8	107,9	95,70	-181,3	-10,80	-10,38	9,485	3,528
C	91,63	-41,42	-27,32	-21,38	-18,82	36,86	2,140	2,053	-1,964	-0,7519
D	-7,973	3,686	2,495	1,862	1,629	-3,288	-0,1863	-0,1788	0,1779	0,0699
E	0,2566	-0,1207	-0,0836	-0,0601	-0,0523	0,1083	0,0060	0,0058	-0,0059	-0,0024
К-ты A …F (7)	Оси ортотропии многоугольника проходят через вершины
	Коэффициенты a … j выражения (5)
	a	b	c	d	e	f	g	h	i	j
Шарнирное опирание (рисунок 2, а)
A	-5,964	1,151	-0,2795	-0,1047	-0,0378	-3,247	0,0043	-0,0208	-0,1053	522,9
B	-0,3634	-0,2622	-0,3328	-0,2713	-0,1143	-0,0360	-0,2764	-0,1090	-0,2403	950,4
C	0,9837	-0,1936	-0,0472	0,0174	-0,0060	0,4261	-0,0007	0,0038	0,0144	-65,76
D	0,0333	0,0162	0,0243	0,0178	0	0	0,0186	0	0	-106,9
Жесткое защемление (рисунок 2, б)
A	15,30	4,619	6,256	-0,5291	-0,2272	-1,40924	0,0202	-0,0036	0,0574	0,1022
B	-0,0890	0,0063	-0,1558	-0,1172	-0,1144	-0,1203	-0,1184	-0,1175	-0,1230	-0,1176
C	-1,161	0,6260	-0,7819	0,0566	0,0202	0,1737	-0,0020	0,0008	-0,0072	-0,0123
D	0	0	0,0039	0	0	0	0	0	0	0

При этом коэффициенты a_n, … , j_n будут изменяться в зависимости от соотношения сторон пластинки. Учитывая это обстоятельство, представим коэффициенты a_n, … , j_n в виде функций , постоянных при заданных граничных условиях, где индекс k соответствует коэффициентам a_n, … , j_n выражения (5), а l – вариантам граничных условий. Неизвестные функции найдем, воспользовавшись программным комплексом Table Curve 2D. По результатам вычислений были получены функции следующего вида для случая, когда одна из осей ортотропии направлена вдоль стороны пластинки (рисунок 1):

; (6)

для случая, когда оси ортотропии проходят через вершины пластинки (рисунок 2), получены выражения следующего вида:

. (7)

Значения коэффициентов A_k,l, …, E_k,l для соответствующих и граничных условий приведены в таблице 1.

Подставляя значения переменных коэффициентов A … F из таблицы 1 в выражения (6) и (7) и заменяя полученными значениями коэффициенты a … j выражения (5), найдём значения функции . Умножив их на размерный множитель , получим значения основных частот собственных колебаний для ортотропных пластинок в виде правильных многоугольников при однородных граничных условиях. Разница между значениями, полученными по аппроксимирующей функции (5) и вычисленными по МКЭ с использованием программного комплекса SCAD, не превосходит 1,51%.

Пример. Рассмотрим пример применения МИКФ к решению задачи о собственных колебаниях восьмиугольной симметричной ортотропной пластинки, шарнирно опертой по контуру (рисунок 3, а). Геометрические параметры очертания пластинки: K_f = 7,204. соотношения цилиндрических жесткостей – . Площадь пластинки A = 1 м².

Заданная форма области может быть получена из правильного восьмиугольника (рисунок 3, б) или прямоугольника (рисунок 3, в) в результате сжатия (растяжения) вдоль оси oy .

Рисунок 3 – Сжатие правильного многоугольника

Для пластинки в виде правильного восьмиугольника с помощью аппроксимирующих функций (5) и (6) при K_f-8 = 6,627 получим ω₁ = 29,87 с^–1. Параметры пластинки в виде прямоугольника: K_f-4 = 11,3137; ω₂ = 43,889 с^–1.

Воспользуемся аппроксимирующей функцией вида:

(8)

Значения неизвестных коэффициентов B и C в (8) найдем, подставляя в это выражение данные для равнобедренного и прямоугольного треугольников:

Подставляя эти значения в (11) имеем:

.

С помощью МКЭ (по программному комплексу SCAD) для заданной пластинки было получено значение основной частоты колебаний в ненагруженном состоянии ω = 30,63 с^–1.

Таким образом, результат вычислений с помощью МИКФ на 3,13% отличается от решения той же задачи с помощью МКЭ.

Заключение

1. Построены аппроксимирующие функции для нахождения значений основной частоты собственных колебаний упругих ортотропных пластинок в виде правильных многоугольников с однородными граничными условиями.

2. Полученные аппроксимирующие функции могут быть использованы для непосредственного расчета пластинок в виде правильных многоугольников и в качестве граничной кривой для выбора опорных решений, а также для разработки программного комплекса, реализующего метод интерполяции по коэффициенту формы при расчёте ортотропных пластинок.

Литература

1. Коробко, А.В. Геометрическое моделирование формы области в двумерных задачах теории упругости [Текст] / А.В. Коробко. – М.: Изд-во АСВ, 1999. – 320 с.

2. Коробко, В.И. Изопериметрический метод в строительной механике: Теоретические основы изопериметрического метода [Текст] / В.И. Коробко. – М.: Изд-во АСВ, 1997. – 390 с.