3.13 Моделирование свойств грунта при определении осадок центрально нагруженных ленточных фундаментов

Прокуров М.Ю., Киреев А.А. (БГИТА, г. Брянск, РФ)

В статье рассмотрены физические модели грунтовых оснований, используемые при расчётах осадок фундаментов. Приведен сравнительный анализ распространённых методов расчёта. Рассмотрен пример реализации расчёта осадки центрально нагруженного ленточного фундамента в линейной и нелинейной постановке.

The physical models of the soils of founding, of a used in calculations of the sediment of the foundations considers in article. A comparative analysis over of widespread methods of calculation is brought. An example of the calculation of sediment central loaded strip foundation in linear and nonlinear formulation of problem is brought.

Определение деформаций грунтов под действием внешних сил имеет большое значение для практики проектирования фундаментов, поскольку точная оценка напряжённо деформированного состояния оснований зданий и сооружений позволяет снизить материальные затраты на устройство фундаментов и сократить сроки строительства. При этом количественное прогнозирование деформаций системы «сооружение – основание» представляет собой одну из наиболее сложных задач механики грунтов, подходы к решению которой носят приближенный характер.

При проектировании конструкций фундаментов необходимо выполнение следующих условий:

(1)

где s  осадка основания фундамента; s_u  предельное значение основания фундамента; p  среднее давление под подошвой фундамента; R  расчетное сопротивление грунта.

Действующими нормами [3] предлагается проводить расчёт осадок с использование модели линейно деформируемого полупространства. При этом в качестве расчётного сопротивления грунта принимается предел среднего напряжения под подошвой фундамента, до достижения которого допустимо определение осадок по формулам теории линейного деформирования.

В настоящее время известен ряд инженерных методов, построенных с использованием указанной расчётной модели. Ниже приведём основные характеристики наиболее распространенных из них.

Метод послойного суммирования (МПС) без учёта возможности бокового расширения грунтов.

Данный метод является основным при расчётах осадок фундаментов зданий и сооружений.

К его достоинствам можно отнести относительную простоту расчёта, которая достигается принятием ряда допущений:

• напряжения в грунтовом массиве не превышают расчётного сопротивления грунта;

• поперечные деформации грунта равны нулю;

• распределение дополнительных вертикальных напряжений по глубине грунтового массива принимается для центрального сечения равномерно загруженной поверхности линейно деформируемого полупространства;

• сжимаемая зона грунтового массива ограничена глубиной, на которой дополнительные давления не превышают 10-20% от веса грунта.

Принятая модель грунтового основания, не учитывающая возможность бокового расширения грунта, даёт заниженную оценку осадки фундамента.

МПС с учётом возможности бокового расширения грунтов

Данная модификация учитывает боковое расширение грунта, достигая более точного значения осадки фундамента ценой некоторого усложнения расчётной процедуры при использовании линейной модели деформирования грунтов основания.

Метод линейно деформируемого слоя.

Находит применение в тех случаях, когда МПС даёт завышенные значения осадок:

• в толще грунтового массива залегает практически несжимаемый грунт с модулем деформации E ≥ 100 МПа;

• ширина фундаментов равна или превышает 10 м;

• под подошвой фундаментов залегает грунт с модулем деформации E ≥ 10 МПа.

Основным отличием данной расчётной модели является то, что глубина сжимаемой толщи ограничивается мощностью рассматриваемого линейно деформируемого слоя грунта.

Метод эквивалентного слоя

По своим теоретическим предпосылкам занимает промежуточное положение между строгими аналитическими решениями и МПС. В отличие от последнего, нивелирующего свойства всех грунтов при учёте бокового расширения, в данном методе используется более обоснованная оценка осадки на основе значения коэффициента Пуассона.

Недостатком данного метода является ограничение площади проектируемых фундаментов до 50 м². Для бóльших значений площади метод эквивалентного слоя не допускает достаточно точных решений.

Анализ рассмотренных методов приведен в таблице 1.

Существующие программные комплексы способны успешно решать задачу определения осадок фундаментов, однако многие из них реализуют указанные методы, использующие линейную модель деформирования грунтов. Учёт нелинейных физических свойств основания может быть реализован в основном на базе универсальных дорогостоящих программных пакетов, работа с которыми требует от пользователя определённого уровня адаптации и практики проектирования. Наиболее популярные из них  Фундамент 12.4, ПК SCAD Office.

Таблица 1  Сравнение расчетных методов определения осадок фундаментов

№ п/п	Метод расчёта	Линейная модель	Учёт поперечного линейного расширения	Большая площадь фундамента	Слабые грунты
1	МПС без учёта бокового расширения грунта	+			+
2	МПС с учётом возможности бокового расширения грунта	+	+		+
3	Метод линейно деформируемого слоя	+		+	
4	Метод эквивалентного слоя	+	+		+

Таким образом, модель линейно деформируемого основания в различных модификациях получила наибольшее распространение среди действующих расчётных методик, используемых при оценке осадок фундаментов.

Однако применение указанного подхода к решению проектных задач зачастую ведёт к следующей ситуации. Чем ближе давление p к расчётному сопротивлению R при выполнении условия s ≤ s_u, тем более экономично запроектирован фундамент. При этом на практике нередки случаи, когда расчётная осадка s оказывается значительно меньше предельной допустимой даже при давлениях, близких к расчётному сопротивлению грунта: s << s_u при p ≈ R. В этом случае для достижения оптимального решения можно уменьшить площадь подошвы фундамента, увеличив среднее давление под подошвой фундамента и тем самым, приблизить расчётную осадку к предельной s ≈ s_u. При этом среднее давление под подошвой фундамента превысит значение расчётного сопротивления грунта p > R и определение осадки фундамента с использованием линейной модели деформирования станет невозможным. В связи с этим возникает необходимость реализации нелинейной модели деформирования грунта для обеспечения рационального проектного решения.

Существенное повышение ресурса несущей способности основания за счёт использования нелинейной модели деформирования грунта наглядно иллюстрируется численными исследованиями величин осадок центрально нагруженных фундаментов, приведенными в научной и учебной литературе.

Рассмотрим пример расчёта осадки центрально нагруженного ленточного фундамента с использованием метода конечных элементов (МКЭ) в линейной и нелинейной постановке [4]. Рассматривается фундамент шириной b = 2 м, глубиной заложения d = 2 м. Нагрузка, приложенная к плоскости подошвы F_v = 580 кН/м. Под фундаментом залегают однородные тугопластичные суглинки. Характеристики грунта в основании: удельный вес γ = 18 кН/м³, угол внутреннего трения φ = 20^°, сцепления грунта c = 20 кПа.

В процессе расчёта проводилось пошаговое увеличение нагрузки ступенями Δ p = 36 кПа, что представляет собой давление от грунта засыпки на проектной отметке фундамента. Для каждой ступени загружения определялась величина осадки основания по центральной оси фундамента.

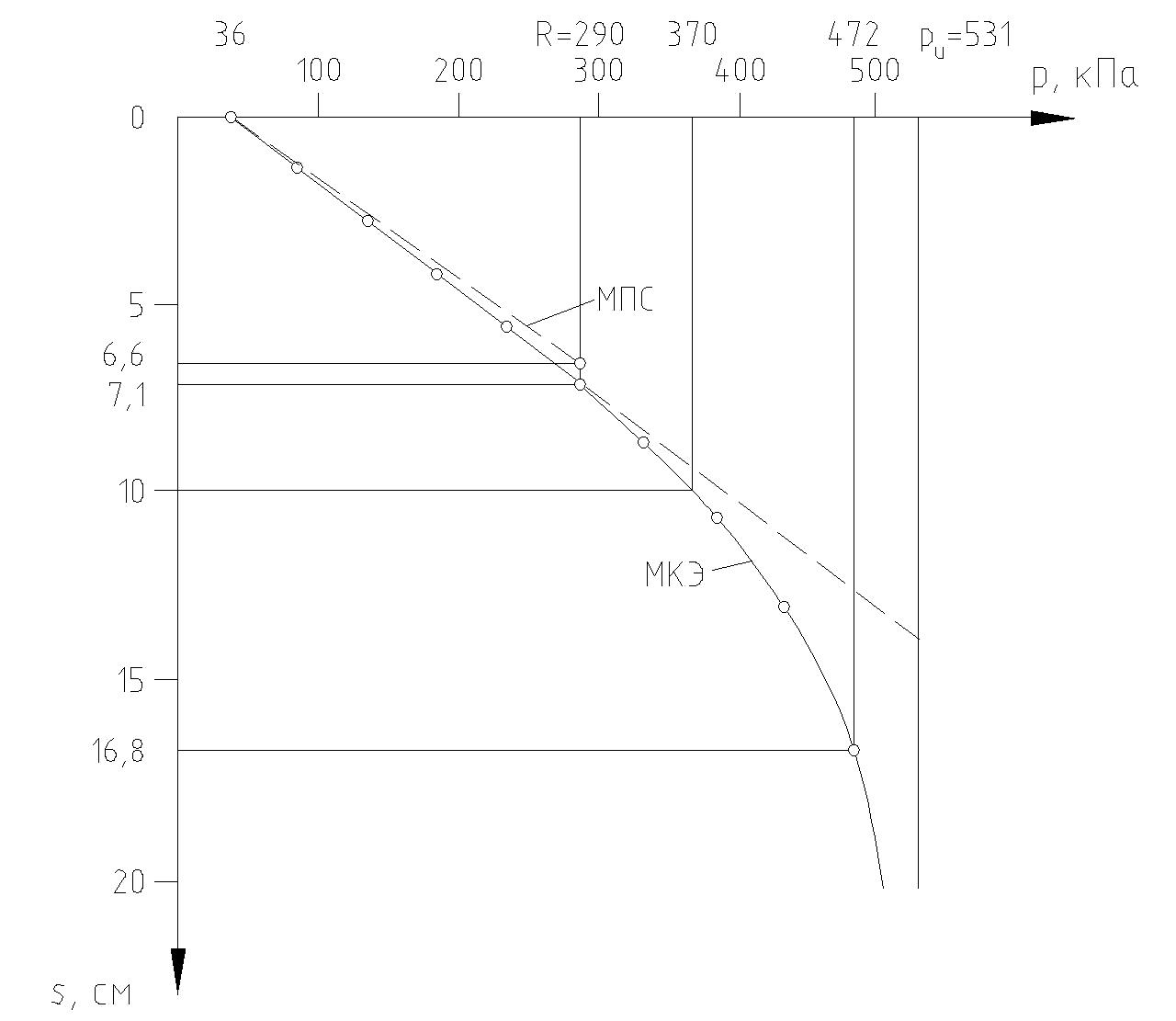
Пошаговая реализация решения с помощью МКЭ, выполненная на базе универсального программного пакета, позволила получить кривую зависимости, представленную на рисунке 1.

Рисунок 1  График зависимости конечной осадки фундамента от прилагаемой нагрузки

Из рисунка 1 видно, что при давлениях под подошвой фундамента, не превышающих природное на уровне его проектной отметки, осадки фундамента практически отсутствуют, так как эти давления прикладываются к основанию, уплотнённому действием собственного веса грунта. Далее осадка возрастает по линейному закону до давления, близкого к расчётному сопротивлению грунта R. При p = R получена осадка s  = 7,1 см, что превышает значение, рассчитанное по МПС s = 6,6 см, так как последним не учитывалось влияние бокового расширения грунта. Аналогичный расчёт осадки рассматриваемого фундамента, выполненный полуавтоматизированным способом путём реализации метода конечных разностей (МКР) [2], определил значение осадки s  = 7,2 см.

Результаты расчётов осадок фундамента при p = R, проведенных различными методами и программными средствами, приведены в таблице 2.

Рассчитанные величины осадок имеют достаточно близкие значения, соответствуя точке предельной упругой деформации грунта основания. Как видно на рисунке 1, полученная осадка соответствует давлению под поверхностью фундамента R = 290 кПа.

Таблица 2  Значения осадок фундамента, полученные различными методами и программами

№ п/п	Метод расчёта	Значение осадки фундамента s, см
1	МПС без учёта бокового расширения грунта	6,6
2	МПС с учётом возможности бокового расширения грунта	7,0
3	Метод эквивалентного слоя	8,3
4	МКЭ [4]	7,1
5	МКР [2]	7,2
6	Программа «Фундамент 12.4»	6,7

При бóльших давлениях график осадки значительно отклоняется от прямой линии, что происходит вследствие развития зон пластических деформаций под подошвой фундамента.

Продолжение расчётной процедуры МКЭ за пределом упругой работы основания позволяет получить полную модель деформирования грунта, представленную графиком зависимости «p – s» на рисунке 1. По построенному графику можно определить давление под подошвой фундамента для установленного нормами предельного значения осадки s_u = 10 см, которому соответствует нагрузка p = 370 кПа. Аналогичный результат достигнут реализацией МКР.

Таким образом, площадь рассматриваемого фундамента может быть уменьшена, что позволяет сократить расход материала на его изготовление практически на 20 %.

Ввиду проиллюстрированного экономического эффекта, представляется актуальным создание специализированного программного обеспечения для расчёта конечных осадок фундаментов с учётом нелинейных свойств грунтов оснований. Построенная с его помощью нелинейная модель деформирования основания позволит определить давление под подошвой фундамента, отвечающее предельно возможному значению осадки. Дополнительно ставится задача создания баз данных грунтов и допустимых значений осадок фундаментов, соответствующих различным типам зданий и сооружений.

Заключение

1. Действующая нормативная база предусматривает прогнозирование конечных осадок оснований фундаментов с использованием модели линейно деформируемого полупространства. За основу существующего программного обеспечения приняты действующие нормы, реализующие модель линейно деформируемого грунта. Нелинейная модель деформирования может быть реализована итерационным расчётом с помощью универсальных программных пакетов, обладающих большой стоимостью и требующих адаптации пользователя.

2. Использование численных методов позволяет построить нелинейную модель деформации основания в виде зависимости «p – s», позволяющую учесть проявление максимально допустимых осадок для оптимального проектирования фундаментных конструкций.

3. Возможный эффект реализации нелинейной модели деформирования приводит к значительному снижению расхода материалов при устройстве фундамента (до 20%), что способствует получению экономического эффекта при типовом строительстве.

Литература

1 Абуханов, А.З. Механика грунтов: Учебное пособие [Текст] / А.З. Абуханов. – Ростов н/Д: Феникс, 2006. – 352 с.

2 Прокуров, М.Ю. Автоматизация расчёта нелинейных осадок ленточных фундаментов с использованием метода конечных разностей [Текст] / М.Ю. Прокуров, Д.А. Бондарев // Молодёжь и XXI век: материалы I Международной молодёжной научной конференции: Ч.2; Курск. гос. техн. ун-т. Курск, 2009. – С. 123-128.

3 СП 22.13330.2011. Основания зданий и сооружений. Актуализированная редакция СНиП 2.02.01-83* – М.: Минрегион России, 2011.  162 с.

4 Ухов, С.Б. Механика грунтов, основания и фундаменты [Текст]: Учебник / С.Б. Ухов, В.В. Семенов, В.В. Знаменский, З.Г. Тер-Мартиросян, С.Н. Чернышев – Москва: АСВ, 1994. – 527 с.