Литература

1. Вознесенский Е.А. Поведение грунтов при динамических нагрузках.- М.: Издательство МГУ, 1997. – 286 с.

2. Ишихара К. Поведение грунтов при землетрясениях. С.Петербург, 2006. – 379 с.

3. Мирсаяпов И.Т., Королева И.В. Футбольный стадион на 45000 зрителей, ул. Чистопольская. Лабораторные динамические исследования грунтов при сценарных землетрясениях площадки строительства объекта. Отчет о научно-исследовательской работе. Казань, ФГОУ ВПО «Казанский государственный архитектурно-строительный университет», 2010г. – 69 с.

4. Ставницер Л.Р. Сейсмостойкость оснований и фундаментов. – М.: Издательство АСВ, 2010. – 448 с.

5. Seed H.B. Soli liquefaction and cyclic mobility evaluation for level ground during earthquakes. Journal of ASCE. 1996. 105, T2, Р. 201-255.

3.8 Расчет элементов из клееной древесины cо стыковкой частью торцов

Михайловский  Д.В., Коваленко М.С. (КНУСА, г. Киев, Украина)

Рассмотрены существующие методики определения изгибающего момента во внецентренно-сжато-изгибаемых элементах с учетом деформированной схемы работы. Предложена и обоснована численным сопоставлением собственная методика определения расчетного изгибающего момента для элементов из клееной древесины cо стыковкой частью торцов.

Данная работа посвящена расчету элементов конструкций из цельной и клееной древесины (верхним поясам ферм) в которых используется конструктивный прием, уменьшающий расчетный изгибающий момент от поперечной внеузловой нагрузки, путем создания разгружающего встречного момента. Суть конструктивного приема состоит в том, что внутреннее продольное усилие в элементах смещается вниз от геометрической оси, что достигается внецентренным стыкованием элементов в узлах. Таким образом, практически без значительных материальных и производственных затрат достигается максимальный экономический эффект. С точки зрения законов развития технических систем данный прием эволюционный.

В существующих нормативных документах 1, 2, 3, 4, как отечественных, так и зарубежных, конкретных указаний по расчету таких элементов не содержится, хотя косвенно говорится о целесообразности использования конструктивного приема, оговоренного ранее.

В нормах и учебно-методической литературе рассматривают лишь сжато-изгибаемые элементы, находящиеся под действием поперечной нагрузки и продольной силы, приложенной по геометрической оси элемента. На такие элементы распространяется методика расчета обычных сжато-изгибаемых элементов, основанная на теории краевых напряжений проф. Завриева К.С. 5. Данная методика расчета достаточно приближенная. Однако, она автоматически перешла на расчет сжато-изгибаемых элементов с внецентренным приложением продольного усилия. В учебно-методической литературе [6, 7, 8] приведены расчеты внецентренно-сжато-изгибаемых элементов с использованием теории проф. Завриева К.С. Однако, следует отметить, что физические явления, происходящие в центрально сжато изогнутых и во внецентренно-сжато-изогнутых элементах отличаются.

В данной работе предложен метод расчета, который, по мнению авторов, адекватно отображает физическое явление внецентренно-сжато-изгибаемых элементов. Ниже приведем его обоснование.

Рисунок 1 - Расчетная схема внецентренно-сжато-изгибаемого элемента

Из сопротивления материалов известно, что прогиб балки у_x (рисунок 1) в состоянии статического равновесия элемента определяется из дифференциального уравнения:

. (1)

Уравнение деформированной оси стержня можно получить, дважды проинтегрировав уравнение (1):

. (2)

В общем случае уравнение изгибающего момента с учетом поперечных деформаций приобретает вид:

. (3)

В формуле (3), для решения дифференциального уравнения (1) следует предварительно задаться уравнением кривой деформированной оси. В [7, 10] предложено в качестве кривой деформированной оси применять тригонометрический ряд Фурье (4), который должен удовлетворять краевым условиям.

(4)

Учитывая тот факт, что при симметричной нагрузке первый член ряда дает точность, равную 95-97%, в дальнейшем ограничимся только им.

Подставив из уравнения (4) в (3) и дважды проинтегрировав (2), получаем уравнение деформированной оси элемента в общем виде. В уравнения вводим краевые условия для заданной расчетной схемы (рисунок 2) и находим постоянные интегрирования. Тогда расчетный прогиб в середине пролета элемента равен:

. (5)

Максимальный расчетный момент находится в середине пролета элемента. Подставив нужную координату сечения и выполнив математические преобразования получаем формулу для определения расчетного момента в внецентренносжато-изгибаемом элементе с учетом деформированной оси:

(6)

Для упрощения расчетных формул (5), (6) заменяем составляющие уравнения условиями для определения изгибающего момента (M_q; M_N) и прогиба (f_q; f_N) в балке на двух опорах под действием равномерно распределенной нагрузки и продольной силы, и параметром U (7). Окончательно получаем запись для определения расчетного изгибающего момента (8) и прогиба (9).

; ; ; ; (7)

(8)

(9)

Полученные формулы (8), (9) точно передают физическое явление, которое происходит в элементах, работающих на внецентренное сжатие с изгибом, в соответствии с расчетной схемой (рисунок 2).

Для сравнения предложенной методики с другими, используемыми в учебно-методической литературе [7, 9, 10, 11], были проведены численные исследования, которые касались определения расчетного изгибающего момента M_розр в панелях верхних поясов ферм. Для возможности сопоставления результатов общая геометрия ферм и нагрузки приняты одинаковыми. Менялся только тип решетки ферм, а соответственно длины элементов и гибкости верхнего пояса. Элементам задавались физико-механические характеристики согласно нормам проектирования: расчетное сопротивление на изгиб - R_зг= R_с=15 МПа (для древесины 2-го сорта); модуль упругости вдоль волокон Е=10000 МПа.

Сравнивались пять методик определения расчетного изгибающего момента с учетом деформированной оси элемента верхнего пояса с внецентренным приложением продольной силы:

І. Методика 11 , (10)

ІІ. Методика 9 , (11)

ІII. Методика 11 , (12)

где f_q – прогиб элемента от действия равномерно распределенной поперечной нагрузки.

IV. Методика 11 , (13)

где f_q – прогиб элемента от действия равномерно распределенной поперечной нагрузки, f_N - выгиб от действия продольной силы.

V. Методика – формула (8).

Результаты численных исследований представлены в виде графика зависимости расчетного момента M_розр от пролета панели верхнего пояса (рисунок 2). Из графика (рисунок  2) четко прослеживается существенное увеличение расхождения расчетных моментов, определенных по разным методикам. Неплохая сходимость всех представленных методик происходит только при незначительных пролетах (до 3-х метров), а соответственно и гибкостях элементов.

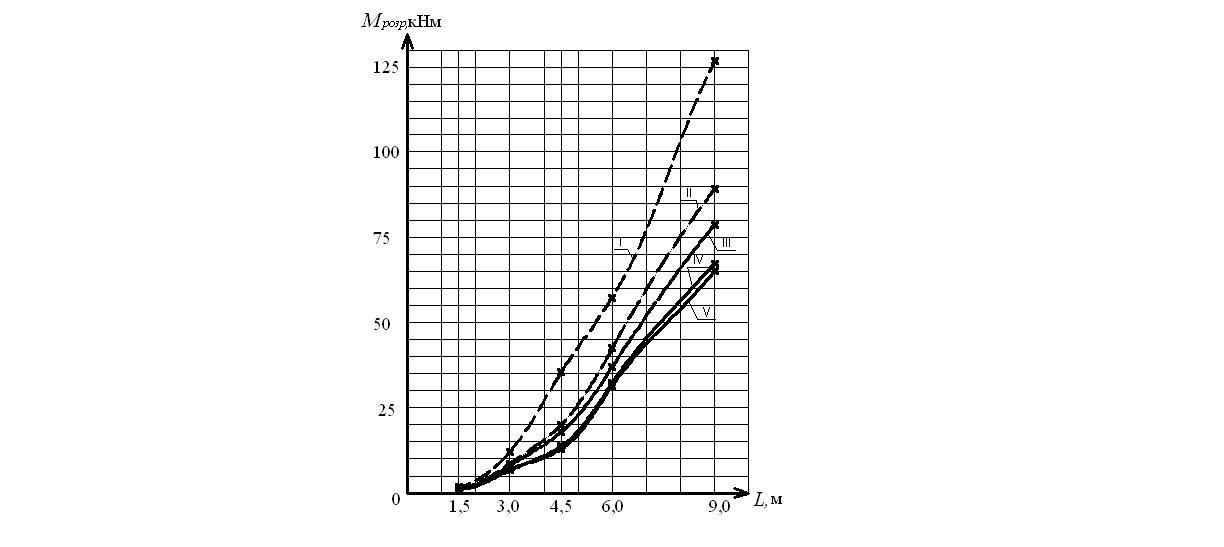
Рисунок 2 - График зависимости расчетного момента от пролета панели верхнего пояса

Р исунок 3 - Графики зависимости напряжения от пролета панели верхнего пояса по предложенным методикам

Результаты исследований показали значительное расхождение предложенной методики расчета (V) с методиками (I, II, III), которые не отражают физическое явление, происходящее во внецентренно-сжато-изгибаемых элементах. Также следует отметить, что разница между методиками IV и V не превышает 7%. Но методика V адекватно формализует физическое явление. Для практических целей можно использовать IV методику, но с корректировкой стандартной формулы для определения f_N.

Формулы (8) и (9) позволяют учитывать реальную работу внецентренно-сжато-изгибаемых элементов с применением современных программных комплексов и получать точные значения изгибающего момента в расчетном сечении. Особенно введение точной методики расчета актуально для современных большепролетных конструкций из клееной древесины.

Заключение

В большепролетных конструкциях из клееной древесины широкое распространение нашел конструктивный прием по стыковке панелей верхних поясов частью торцов с целью уменьшения расчетного изгибающего момента от внеузловой нагрузки. В нормативных документах и учебно-методической литературе не содержится конкретных рекомендаций относительно определения расчетного изгибающего момента в таких элементах. Предложенная в данной работе методика позволяет достаточно точно определять расчетный момент во внецентренно-сжато-изгибаемых элементах с учетом деформированной схемы, что даст возможность рационально проектировать современные большепролетные конструкции из клееной древесины.

Литература

1. Деревянные конструкции: СНиП ІІ-25-80. – М. : Стройиздат – Госстрой СССР, 1982. – 66 с.

2. СП 64.13330.2011 Деревянные конструкции. Актуализированная редакция СНиП II-25-80. – ОАО «ЦПП» – Москва, 2011. – 87 с.

3. Деревянные конструкции: СНБ 5.05.01-2000. – Министерство архитектуры и строительства Республики Беларусь – Минск, 2001. – 70 с.

4. ДБН В.2.6-161:2010 «Конструкції будинків і споруд. Дерев’яні конструкції. Основні положення» - К. "Укрархбудінформ" 2010. – 109с.

5. Завриев К.С. Расчет стержней на одновременное действие изгиба и осевого сжатия. – Тифлис. – 1932.

6. Иванов В.Ф. Конструкции из дерева и пластмасс. Учебник для вузов/ В.Ф. Иванов – Л.: Стройиздат, 1966. – 352 с.

7. Конструкции из дерева и пластмасс. Учебник для вузов. / [Карлсен Г. Г., Большаков В. В., Каган М. Е. и др.] Под ред. Карлсена Г. Г. [4-ое, изд. перераб. и доп.] – М. : Стройиздат, 1975. – 688 с.

8. Гринь И.М. Строительные конструкции из дерева и синтетических материалов. Проектирование и расчет: Учеб. пособие для строительных вузов и ф-тов./ И.М. Гринь – 2-е изд., перераб. и доп.– Киев – Донецк: Вища школа, 1979. – 272 с.

9. Серов Е.Н. Проектирование клееных деревянных конструкций: Учеб. пособие. Ч. IIІ. Проектирование рам с криволинейными участками и арок / Е.Н. Серов, Ю.Д. Санников; Под ред. Е.Н. Серова;. СПб гос. архит.- строит. ун-т. – СПб., 1999. – 160 с.

10. Конструкции из дерева и пластмасс. Учебник / [Гаппоев М.М., Гуськов И. М., Ермоленко Л.К. и др.] – М.: Издательство АСВ, 2004, – 440 с.

11. Кліменко В.З. Проектування дерев’яних конструкцій: Навч. посібник / В.З. Кліменко. – К.: ІЗМН, 1998. – 432 с.