3.5 Анализ начальной надежности железобетонных конструкций со сложным напряженным состоянием

Коваленко Г.В., Жердева С.А., Мартынов С.В. (БрГУ, г. Братск, РФ)

В данной статье представлены результаты анализа начальной надежности железобетонных конструкций, испытывающих сложное напряженное состояние. Приведены требуемые уровни надежности железобетонных конструкций. Проведено сопоставление экспериментальных и расчетных данных, полученных при моделировании по разработанным программам.

This article presents an analysis of the initial reliability of reinforced concrete structures, experience complex stress state. Shows the required level of reliability of reinforced concrete construction. A comparison of experimental and calculated data obtained in the simulation by the developed program.

При производстве сборных железобетонных конструкций основной задачей является обеспечение эксплуатационной пригодности выпускаемой продукции с минимальными затратами. Одним из решений этой задачи является создание системы технологического контроля и управления качеством, обеспечивающей управление основными этапами технологического процесса изготовления деталей и конструкций.

На данный момент, в соответствии с действующими стандартами на заводах ЖБИ ведется текущий контроль отдельных показателей качества (геометрические параметры конструкции, характеристики прочности и деформативности материалов, и т.д.). Но, несмотря на это, следует отметить, что по результатам текущего контроля отдельных показателей вывода о надежности конструкций в целом не делается. Поэтому на заводах ЖБИ с целью проверки эксплуатационной пригодности проводят периодические контрольные испытания натурных конструкций на контрольную нагрузку, больше расчетной (ГОСТ 8829-94).

В современных условиях стоимость проведения испытаний при контроле отдельных показателей качества гораздо ниже, чем стоимость проведения контрольных испытаний самих конструкций. В связи с этим назревает решение задачи интегральной оценки надежности конструкций на стадии изготовления по результатам дифференцированного контроля отдельных показателей качества, которая может быть решена с использованием вероятностных методов, оценивающих влияние технологических параметров и их изменчивости на потребительские свойства выпускаемой продукции.

Как известно, характер нагружения оказывает существенное влияние на напряженно-деформированное состояние тела. Сложное напряженное состояние возникает при косом изгибе и косом внецентренном сжатии. Косой изгиб возникает при действии на конструкцию нагрузок в 2-х плоскостях, например, в стеновых панелях [1] при совместном действии вертикальной и горизонтальной нагрузок (от собственного веса и ветровой). Косое внецентренное сжатие возникает в колоннах при наличии эксцентриситетов сжимающей силы относительно двух осей в поперечном сечении элемента. Также косое внецентренное обжатие может возникнуть в момент отпуска напрягаемой арматуры в нижнем поясе фермы, что неблагоприятно сказывается на развитии дальнейшего напряженно-деформированного состояния данной конструкции в стадии эксплуатации.

Для достоверной оценки напряженно-деформированного состояния железобетонных конструкций при сложном напряженном состоянии необходимо правильно выбрать математическую модель работы конструкции при нагружении (статическом или динамическом). При этом следует учитывать, что железобетон - это упруго-пластический материал, обладающий в стадии, близкой к разрушению, значительными пластическими деформациями. Как было доказано выше, а также как следует из теоретических и экспериментальных исследований, адекватно оценить фактическое напряженно-деформированное состояние железобетонных конструкций можно только с помощью математической модели, учитывающей нелинейность характера поведения конструкции, в частности, физическую нелинейность материалов. Это обеспечивается при математическом моделировании напряженно-деформированного состояния железобетонных конструкций с помощью введения в расчетный алгоритм фактических диаграмм деформирования материалов (бетона и арматуры), полученных при обработке экспериментальных данных для исходных классов бетона и арматуры.

Проверка адекватности выбранной математической модели по исследованию сложного напряженно-деформированного состояния железобетонных конструкций осуществляется путем сопоставления экспериментальных данных с учетом их изменчивости и границ доверительного интервала, построенной для данной модели на основе вероятностного алгоритма [2].

Исходя из выше сказанного, вероятностные модели позволяют оценить адекватность выбранной математической модели по исследованию напряженно-деформированного состояния железобетонных конструкций и получить показатели надежности конструкции, по которым оценивается эксплуатационная пригодность конструкций на разных этапах жизненного цикла: стадии проектирования, изготовления и эксплуатации [3].

Основными критериями при оценке надежности железобетонных конструкций при косом внецентренном сжатии [4] принимают следующие показатели:

а) начальная надежность по прочности конструкции Н₀;

б) надежность конструкции в стадии эксплуатации Н₁;

в) оценка эксплуатационной пригодности здания или сооружения по трещиностойкости Н₂;

Важным вопросом является назначение величин Н₀, Н₁, Н₂, определяющих материалоемкость исследуемых конструкций. На основании расчетных прочностных характеристик материалов, приведенных в нормах проектирования железобетонных конструкций, определены уровни надежности по каждому предельному состоянию, которые согласно работ [5, 6] можно принять за требуемые (см. таблицу 1).

Таблица 1 – Требуемые уровни надежности

H0	H1	H2
0,9986	0,9986	0,90

Следует отметить, что при оценке надежности конструкции необходимо задаться законом распределения случайных величин, назначить их статистический характер и выбрать оптимальный метод вероятностного расчета. Существует несколько методов для оценки надежности конструкции, но наиболее эффективными методами для разработки вероятностных алгоритмов являются методы: линеаризации функций, статистического моделирования (Монте-Карло), статистических испытаний и др.

Для вероятностной оценки начальной надежности стеновых панелей, работающих на совместное действие вертикальных и горизонтальных нагрузок, на кафедре строительных конструкций написаны и зарегистрированы в Роспатенте две программы:

• на основе метода линеаризации функций STENA (свидетельство об официальной регистрации программы № 2002611465);

• по методу статистического моделирования на основе нелинейно-деформационной модели NARSTEN (свидетельство об официальной регистрации программы № 2008611474).

Программы осуществляют оценку начальной надежности стеновых панелей по основным контрольным показателям: по прочности, жесткости и трещиностойкости.

Адекватность разработанных вероятностных алгоритмов установлена сопоставлением результатов вычислительного и натурного экспериментов по оценке надежности стеновых панелей. Испытание натурных конструкций проводилось на комбинате «Братскжелезобетон» при непосредственном участии одного из авторов работы профессора Г.В. Коваленко.

Программы реализованы с помощью алгоритмического языка Visual Basic 5.0 (Copyright © 1987-1999 Microsoft Corp.). Для ее отладки выполнен тестовый проверочный расчет стеновой панели по серии 1.432–14 марки ПС 60.12.25 5Л 31Ф. Сечение выбранной стеновой панели и ее армирование соответствуют данной серии [4]. Расчет выполнялся по фактическим характеристикам бетона и стали, полученным при испытании натурных образцов бетона и арматуры.

В результате натурных испытаний определялись фактические значения разрушающих нагрузок (первая группа предельных состояний) и фактические значения прогибов и ширины раскрытия трещин при контрольной нагрузке по жесткости и трещиностойкости (вторая группа предельных состояний).

Выходными данными компьютерной программы, реализующей вероятностную математическую модель, являются значения предельного усилия, воспринимаемого конструкцией, прогибы и ширина раскрытия трещин при контрольной нагрузке с учетом их статистической изменчивости. Для каждого из расчетных параметров строится доверительный интервал с обеспеченностью 0,98.

Сопоставление экспериментальных и расчетных данных по оценке эксплуатационной пригодности приведены в таблицах 2-4.

На рисунке 1 показаны динамика развития прогибов и трещин для исследуемой конструкции. На график нанесены экспериментальные и расчетные значения прогибов и ширины раскрытия трещин, вычисленные по разным моделям: по нормативной на основе метода предельных состояний; по нелинейно-деформационной модели на основе реальных диаграмм деформирования материалов (DIASTEN). На графиках показаны границы доверительного интервала изменения контролируемых параметров с учетом обеспеченности 0,98.

Таблица 2 – Данные по оценке несущей способности панелей

Марка панели	Нагрузка,
	контрольная по прочности		фактическая разрушающая		разрушающая по СНиП		разрушающая по деформационной модели
	верт	гориз	верт	гориз	верт	гориз	верт	гориз
ПС 60.12.25-5Л-31Ф1	27,80	19,74	33,80	23,44	19,93	12,90	29,0	20,0
ПC 60.18.25-6Л-44Ф1	29,90	29,90	29,90	29,88	18,99	17,67	24,08	19,57
ПС 600.12.30	26,36	7,58	26,36	7,58	26,28	7,56	25,01	5,33
ПС 60.12.30-3Л-31Ф1	21,80	7,80	32,59	13,82	27,54	7,24	30,91	13,39
ПС 600.12.25-П1	22,0	7,30	22,0	7,58	19,44	8,55	20,75	6,55

Таблица 3 – Параметры при оценке горизонтальных прогибов

Марка панели	Прогиб,
	контрольный прогиб	фактический прогиб	расчетное значение
			по СНиП	по деформационной модели
ПС 60.12.25-5Л-31Ф1	18,70	20,40	19,18	17,87
ПC 60.18.25-6Л-44Ф1	18,30	8,02	20,16	7,57
ПС 600.12.30	2,20	1,11	0,52	1,63
ПС 60.12.30-3Л-31Ф1	2,50	2,10	1,37	3,17
ПС 600.12.25-П1	6,50	1,71	1,34	2,57

Таблица 4 – Данные ширины раскрытия трещин в горизонтальном сечении

Марка панели	Ширина раскрытия трещин,
	контрольная ширина раскрытия	фактическая ширина раскрытия	расчетное значение
			по СНиП	по деформационной модели
ПС 60.12.25-5Л-31Ф1	0,25	0,19	0,23	0,15
ПC 60.18.25-6Л-44Ф1	0,25	0,20	0,21	0,0
ПС 600.12.30	0,25	0,20	0,0	0,0
ПС 60.12.30-3Л-31Ф1	0,25	0,15	0,0	0,0
ПС 600.12.25-П1	0,25	0,12	0,0	0,0

Анализируя график развития прогибов исследуемых конструкций несущих стеновых панелей, можно выделить два участка деформирования конструкций при кратковременном нагружении:

- участок до образования трещин, на котором наблюдается практически линейное развитие прогибов;

- участок после образования трещин, характеризующийся значительным развитием пластических деформаций и резким нарастанием прогибов и соответственно трещин.

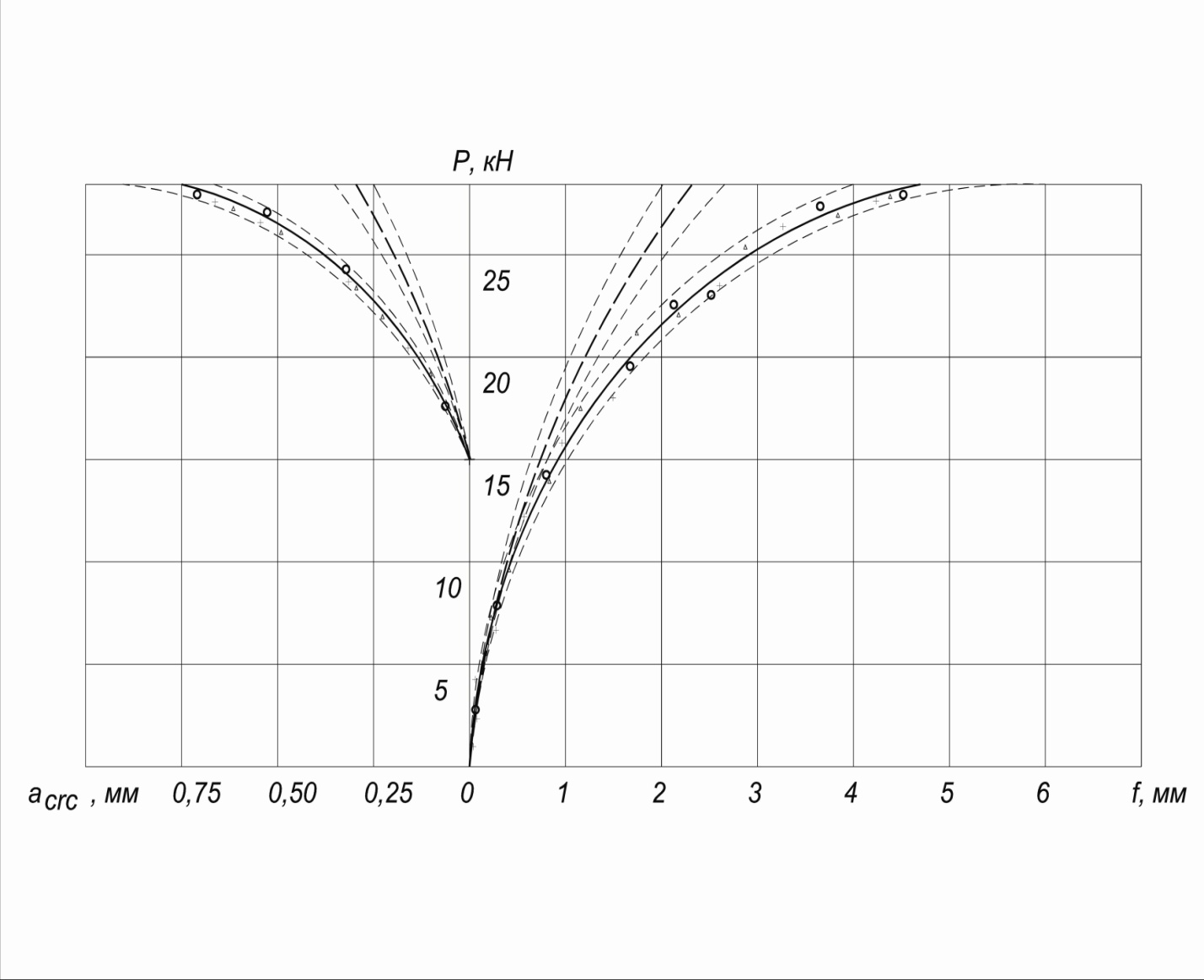
Рисунок 1 - График развития прогибов и трещин от вертикальной нагрузки

для панели ПС 60.12.25-5Л-31Ф1

На пером этапе деформирования обе расчетные модели (нормативная и нелинейно-деформационная) удовлетворительно описывают напряженно-деформированное состояние исследуемой конструкции при кратковременном нагружении. Экспериментальные значения прогибов попадают в доверительный интервал обеих расчетных моделей. Начало второго этапа соответствует нагрузке, контрольной по жесткости и трещиностойкости, что примерно совпадает с нормативной нагрузкой.

Следовательно, для оценки надежности конструкций заводского изготовления будут пригодны обе модели, тем более что оценка прочности по этим моделям также практически совпадает с экспериментальным значением разрушающей нагрузки.

На втором этапе деформирования, характеризующимся значительным появлением нелинейных свойств железобетона, нелинейно-деформационная модель более адекватна фактическому напряженно-деформированному состоянию испытанных конструкций: экспериментальные значения прогибов и трещин попадают в доверительный интервал, полученный на основании вероятностного расчета по нелинейной модели. Расчет по нормативной модели занижает по сравнению с фактическими значениями величину прогиба и ширину раскрытия трещин в предельном состоянии в среднем в 1,5 раза.

Таким образом, при сопоставлении натурного и численного экспериментов для несущих однослойных стеновых панелей результаты исследований следующие:

• в соответствии с действующими нормами, построенными на приближенных принципах, не представляется возможным описать наиболее достоверно напряженно-деформированное состояние конструкции. Поэтому для более полного анализа НДС однослойных стеновых панелей выбрана расчетная модель, предложенная В.Н. Байковым, Н.И. Карпенко, которая учитывает физическую и геометрическую нелинейность с помощью реальных диаграмм деформирования бетона и арматуры;

• существенным достоинством нелинейно-деформационной модели по сравнению с нормативной является то, что она позволяет установить величину деформаций и напряжений по всей высоте сечения в бетоне и в арматуре на каждом этапе кратковременного нагружения;

• нелинейно-деформационная модель наиболее близка к экспериментальным данным (табл. 2-4), т.е. более точно описывает прочность, деформативность, образование и раскрытие трещин при кратковременном нагружении, а также позволяет вести расчет конструкций с единых позиций при сложном напряженном состоянии;

• поскольку адекватность нелинейно-деформационной модели по описанию напряженно-деформированного состояния конструкций при косом изгибе (частного случая косого внецентренного сжатия) установлена сравнением экспериментальных и расчетных параметров на примере однослойных стеновых панелей, она может быть со столь же высокой степенью достоверности быть применима и к колоннам, как при простом, так и при косом внецентренном сжатии.

Литература

1. Крылов, С.Б. К расчету стеновых панелей // Бетон и железобетон. – 2009. - №5. – С. 18-23.

2. Чирков, В.П. Прикладные методы теории надежности в расчетах строительных конструкций. Учебное пособие для вузов ж-д транспорта / В.П. Чирков. – М.: Маршрут, 2006. – 620с.

3. Знаменский, Е.М. О расчете конструкций с заданным уровнем надежности / Е.М. Знаменский, Ю.Д. Сухов // Строительная механика и расчет сооружений. – 1987. - №2. – С. 7-9.

4. Коваленко, Г.В. Результаты исследования напряженно - деформированного состояния стеновых панелей по разным расчетным моделям // Вестник Томского государственного архитектурно-строительного университета. – 2009. - № 2. – С. 91-96.

5. Райзер, В.Д. Теория надежности в строительном проектировании // Монография / В.Д. Райзер – М.: Изд-во АСВ, 1998, - 304с.

6. Дудина, И.В. Обеспечение качества сборных железобетонных конструкций на стадии изготовления/ И.В. Дудина, А.Г. Тамразян // Жилищное строительство. -2001. -№3. - С.8-10.