Комплексний (символічний) метод. Загальні поняття

Ė, Ů, Ǐ – комплексне діюче значення.

Ėm, Ům, Ǐm – комплексне амплітудне значення.

Z - комплексний повний опір.

R – активний опір.

+jXL – комплексний реактивний індуктивний опір.

–jXс - комплексний реактивний ємнісний опір.

Y – комплексна повна провідність.

+jBL – комплексна реактивна індуктивна провідність.

–jBс - комплексна реактивна ємнісна провідність.

S – комплексна повна потужність

Крапка означає функцію, яка змінюється по синусоїдному закону.

Риска означає функцію, яка не змінюється за законом синуса (скалярна величина).

Будь-яку синусоїдну чи скалярну функцію можна представити у комплексній формі.

ј =√-1 ј² = -1

Á = - показникова форма запису.

+j - формула Ейнера.

a Á З цієї формули:

φ a2 А = а·cosφ + j a sinφ = a1 + ja2 = a<α

– 0 a1 +

тригонометрична алгебраїчна полярна

–j форма форма форма

Комплексне число – число, модуль якого являє собою гіпотенузу прямого трикутника.

З прямокутного трикутника:

Якщо множимо або ділимо, то показникова форма. Якщо додаєм

чи віднімаємо, то алгебраїчна форма. Якщо вилучення чи під –

несення до степеня, то показникова форма.

Комплексний опір та комплексна провідність

u = Um sin (ωt + φu)

i =Im sin (ωt + φi)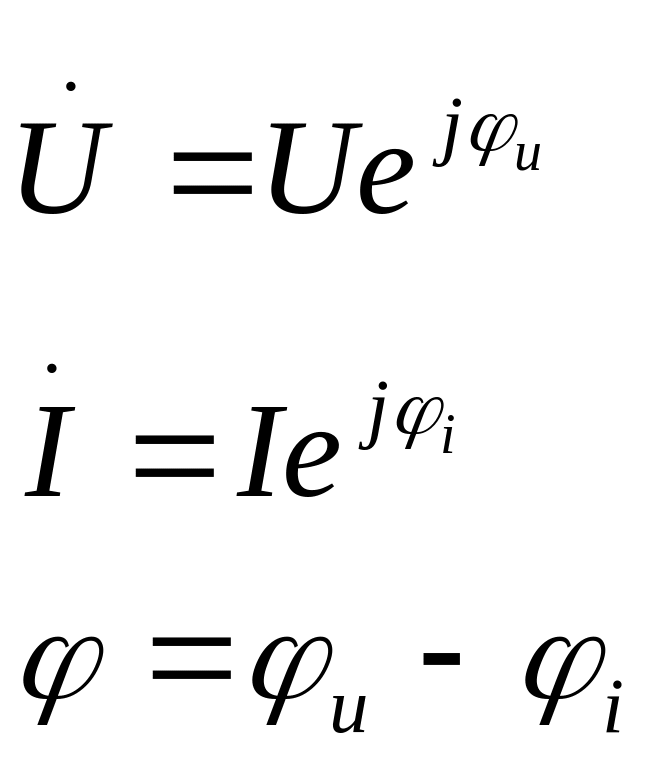

Я кщо „а+jx”, то індуктивний опір, якщо „а – jx”, то ємнісний опір.

Комплексна повна потужність

u = Um sin (ωt + φu)

i =Im sin (ωt + φi)

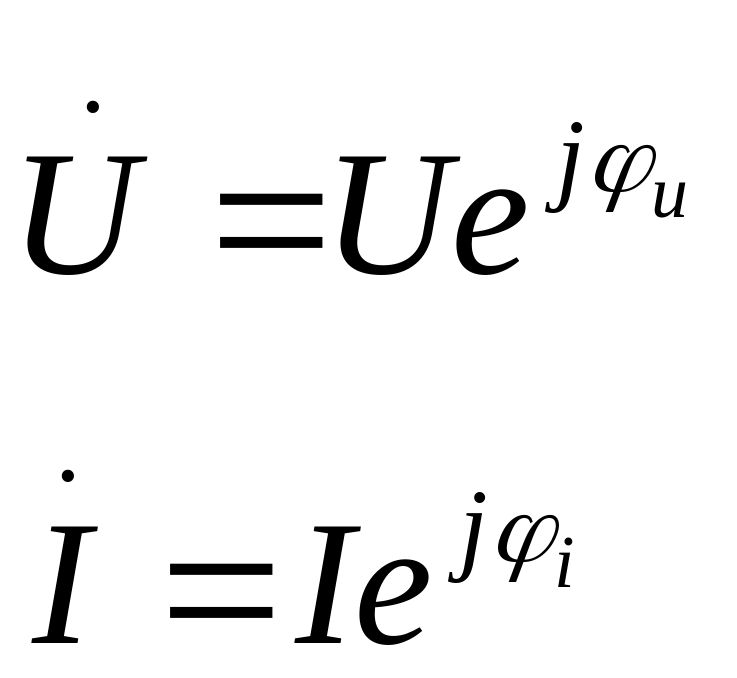S = UI S = [BA]

S = ŮĬ – спряжений комплекс

Розрахунок кіл

Представивши ЕРС струму і напруги і параметри кола в комплексній формі для розрахунку кола можна використовувати без будь-яких обмежень методику розрахунку кіл постійного струму.

Задача

I2

Z1

I1 Z2

S = Ů Ĭ1

U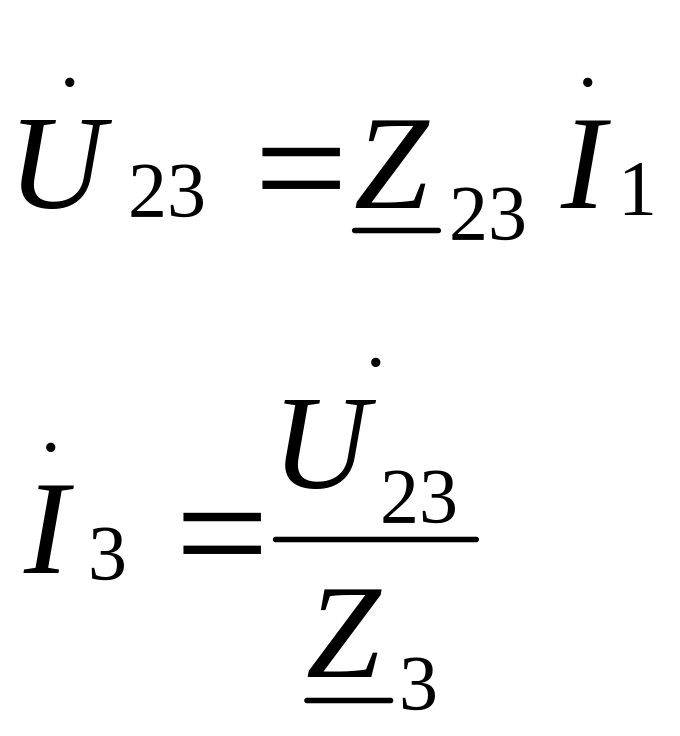

I3 Z4

Z1 = R1 + jX1

Z3 = R3 + jX3

Z2 = R2 – jX2

Ů = Ue’º______

Ĭ1, Ĭ2, Ĭ3, Ů23, S