Резонанс в реальному контурі
І
І1
І2
Вхідна
реактивна провідність повинна бути
рівна нулю.
Для розрахунку кола треба перейти на еквівалентну заміну.
R1 R2
U ВL = Bc
ВL = XL/Z1² =Хс/( R1² + XL²) = ωL/( R1² + (ωL)² )
X1 X2 Вс = Xс/Z2² = Хс/( R2² + Xс²) = (1/ωС)/ ( R2² + (1/ωС)² )
(ωL) /( R1² + (ωL)² ) = (1/ωС)/ ( R2² + (1/ωС)² )
Розв’язавши цю рівність, отримаємо:
ω0´
= 1/
=
ω0’ – частота коливань реального контура.
1
)
Підкореневий вираз не може бути
комтинсним:
> R1,
або
< R1
I
І
> R2
< R2
І
І2с
ω І2
2)Якщо ω0’= ... √-1 – резонанс неможливий. 0 ω
3)Якщо ω0’= 0/0 (тобто ρ = R1= R2 ) – резонанс спостерігається Іа2 Іа1 Іа
у
всьому діапазоні частот. Коло має чисто
реактивний характер.
0
Будуємо векторну діаграму.
І12 І1
L
Задача
В мережу змінного струму послідовно ввімкнено
R C резистор і конденсатор. Визначити індук -
X тивність котушки, яку треба ввімкнути в коло
щоб при f = 200Гц виник резонанс, а також
напругу на конденсаторі до і після вмикання котушки.
u = 169sin (ωt - 90º) Z = Um/Im = 169/5,64 = 29,9 ≈ 30 (Ом)
I = 5,64 sin (ωt - 90º)__
L0, Uc, Uφi = ( - 90º) – ( - 30º) = - 60º
R
φ
Xc
Xc
= Zsinφ
= 30sin
(-60º) = 30(-√2/2) = -15√3 ≈ 26
Z Uc = XcI = 26· 5,64 / √2 = 146,64 √2 = 104 (B)
Xc0 = XL0; XL0 = 26; ω = 2πf = 3,14· 400 = 1256
Xc = Xc0; ωL0 = 26; L0 = 26/1256 = 0,02(Гц)
I0 = U/R = (169/√2)/Zcosφ =(169/√2)/30cos(-60º) = 119,8/30·½ = 8 (A)
Uco = XcI0 = 26·8 = 208 (B)
З
адача
В колі, що складається з котушки і конденсатора
без витрат при резонансі, визначити напругу на
затискачах
цього кола.
Uco
ULa U Lo ULp
U
Lo = 125 (B) ULp
U
co
Uco = 110 (B) __ 0
U0 - ? ULa
XL Задача
R´
Xc
Xc
X´
R
Xc =20 Oм
f = 50
Гц
R = 50 Oм__
L0 - ?
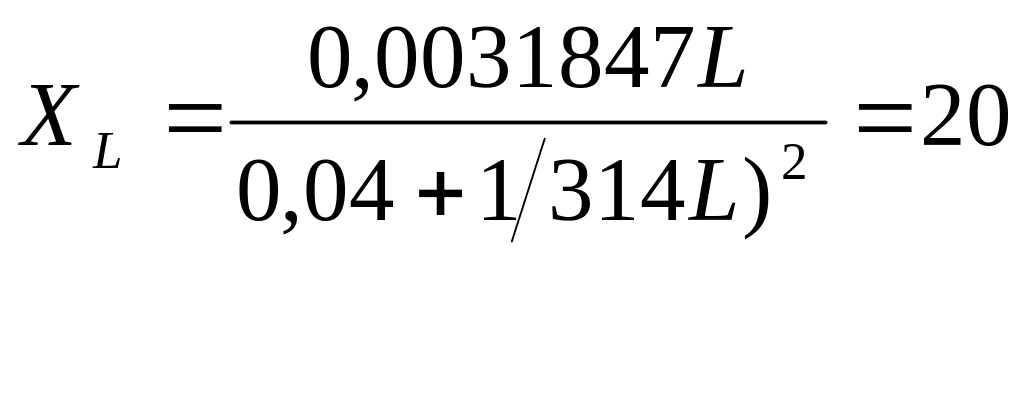
0,0031847L = 20(0,04+ 1/314² · L²); 0,0031847L = 0,8 + 20/314² L² = 0,8 + 20/98596 L = 0,8 + +0,0002028 L²; 0б000208 L² - 0,0031847 L + 0,8 =0