Коливання потужності в колі синусоїдного струму

1. Ідеалізований активний опір

p – миттєва потужність

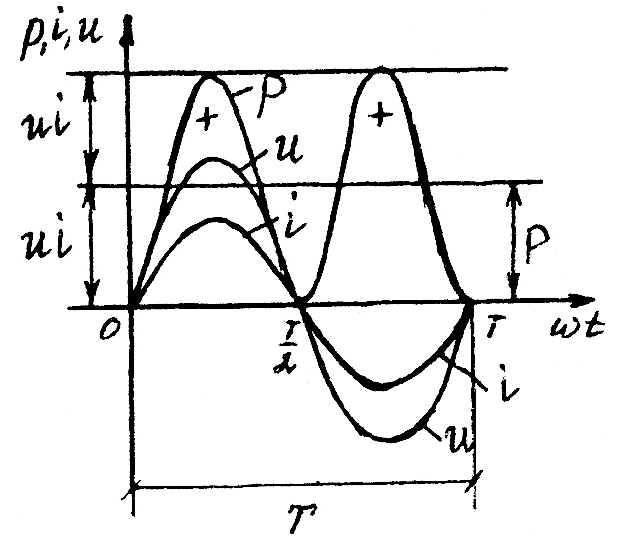
p= UI(1 – cos2ωt) = UI - UIcos2ωt

В ідеалізованому активному опорі електрична

енергія, спожита від мережі, спричиняє

нагрівання резистора, отже виділяється

у вигляді теплової енергії. Потужність

змінюється з частотою у два рази більшою за

прикладену частоту струму і напруги.

2) ідеалізована індуктивність

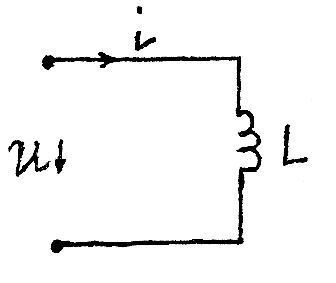u = U_msin(ωt + π/2)

I = I_msin ωt

P = u ∙ I = U_mI_msin(ωt + π/2) =

= U_mI_msinωt cosωt = 2UIsinωt cosωt =UI sin2ωt

sinωt + π/2 = cosωt ; 2sinωt cosωt = sin2ωt

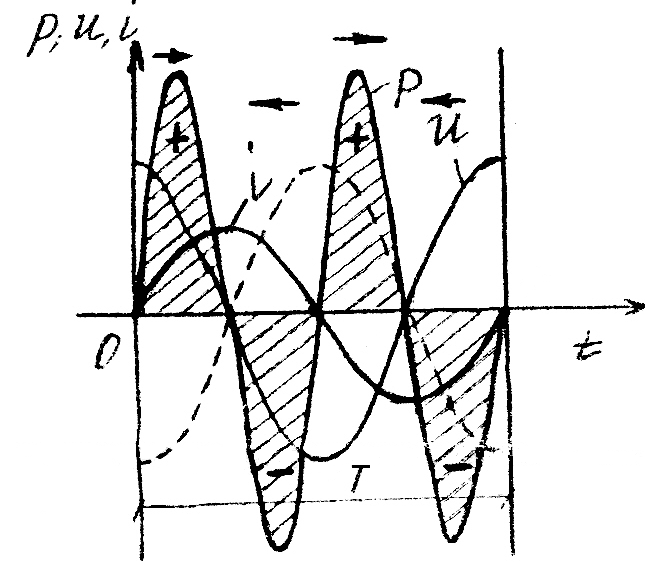
→ використовує енергію

← віддає енергію (джерело)

u_L= L di/dt

p = u_L∙ i = Li di/dt

Якщо перша похідна струму додатня, то потужність додатня (якщо характеристика в абсолютному значенні зростає, то похідна додатня, якщо спадає, то від`ємна).

Четверть періоду, коли миттєва потужність додатня, відбувається процес зарядки котушки індуктивності, в іншу чверть періоду, коли р від`ємна, відбувається розрядка котушки з віддачею енергії в мережу. Оскільки середнє значення потужності за період рівне нулю (активна потужність), то корисна робота не виконується.

W_E= L I_m²/2

3) ідеалізована ємність

u = U_m sinωt

i = I_m sin(ωt + π/2)

p = u · i = U_mI_msinωt sin(ωt + π/2) = U_mI_msinωt cosωt

На основі випадку 2

p = UI sin2ωt

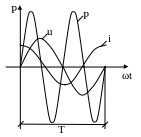
Якщо миттєві значення напруги і струму додатні, то потужність додатня, якщо різнойменні , то від'ємна.

і_с = с і = с u_c =

p = u · i = c · u

Якщо перша похідна струму додатня, то потужність додатня.

Середнє значення потужності за період рівне нулю (активна потужність), корисна робота не виконується.

Енергія електричного поля W_E = c

4 ) реальна котушка, яку можна представити двома схемами заміщення (послідовною і парною)

{

Закон зміни напруги опереджує закон зміни струму.

u = U_т sin(ωt +φ) u = U_т sin ωt

i = I_т sin ωt i = I_т sin(ωt - φ)

φ – кут зсуву фаз між векторами u і i

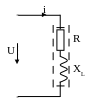p = u · i = I_т U_т sin(ωt +φ) sin ωt = UI(cos φ – cos(2ωt +φ)

2sinα sinβ = cos(α – β) - cos(α + β) I_т U_т = 2UI

p = UIcos φ – UIcos(2ωt +φ)

Визначимо середнє значення потужності за період:

P = UIcos φ dt = UIcos φ – активна потужність

[P] = 1 Вт

З ∆ потужностей:

Q = UIsin φ Q = 1 ВАр

S = S = 1 ВА

S² = P² + Q²

φ = arctg

S = UI

Активна потужність – середнє значення миттєвої потужності за період.