2.2. Системи масового обслуговування з відмовами

Математична модель СМО з відмовами. Багатоканальна система масового обслуговування з відмовами визначається такими параметрами. Система має n однотипних каналів обслуговування. На вхід системи надходить пуассонівський потік однорідних заявок з інтенсивністю . Це означає, що проміжок часу між сусідніми заявками є випадкова величина, розподілена за експоненціальним законом зі щільністю розподілу Середній проміжок часу між сусідніми заявками дорівнює u=1/. Обслуговування заявок здійснюється протягом випадкового часу, розподіленого за експоненціальним законом з параметром , тобто потік обслужених заявок є також пуассонівським з інтенсивністю , а середній час обслуговування дорівнює t_обс=1/.

Обслуговування заявок здійснюється таким чином. Якщо заявка застає усі канали зайнятими, то вона одержує відмову і покидає систему необслуженою. Якщо, заявка застала вільним хоча б один канал, вона приймається на обслуговування будь-яким із вільних каналів.

Таким чином маємо СМО з параметрами:

● кількість каналів обслуговування n;

● інтенсивність потоку заявок на обслуговування дорівнює λ;

● інтенсивність обслуговування кожним каналом дорівнює ;

Необхідно визначити стаціонарні імовірності станів системи, а також її операційні характеристики (характеристики ефективності обслуговування):

● імовірність відмови у обслуговуванні заявок (імовірність втрати заявок);

● відносну та абсолютну пропускну спроможності системи;

● середнє число зайнятих каналів;

● імовірність зайнятості каналів;

● середній час зайнятості каналу;

● середній час повного завантаження системи;

● середній час неповного завантаження системи.

Якщо під розуміти стани системи, коли в ній знаходиться k заявок, то дана система може перебувати в одному із станів

Діаграма інтенсивностей переходів системи має вигляд:

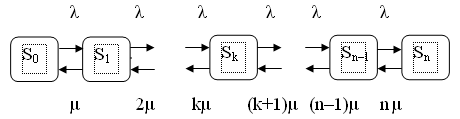
Рис. 2.1. Діаграма iнтенсивностей переходів системи

Позначимо через імовірність того, що в будь-який момент часу система буде знаходитись у стані . Задача полягає у тому, щоб одержати рівняння, яким задовольняють стаціонарні ймовірності і визначити ці ймовірності.

Використовуючи рівняння Колмогорова, покладаючи в них будемо мати систему алгебраїчних рівнянь:

(2.1)

Ту ж ідею складання рівнянь за допомогою діаграми iнтенсивностей переходів можна застосувати і для складання рівнянь рівноваги. У стаціонарному режимі, очевидно потік повинен задовольняти умові збереження потоку у тому смислі, що у кожному стані вхідний потік повинен бути рівним вихідному потоку. Із діаграми видно, що якщо розглянути стан в усталеному режимі, то будемо мати:

● інтенсивність потоку у стан дорівнює ,

● інтенсивність потоку із стану дорівнює

У стані рівноваги ці два потоки повинні бути рівними, і тому одержуємо співвідношення аналогічне (2.1)

Це і є алгебраїчні рівняння для ймовірностей станів. Розв’язок системи рівнянь має вигляд:

(2.2)

Із цієї формули видно, що усі ймовірності виражаються через єдину невідому константу Остання рівність у системи рівнянь (2.1) дає додаткову умову, яка дозволяє визначити Підсумовуючи по всім k, одержуємо

. (2.3)

Введемо позначення =/. Ця величина називається коефіцієнтом навантаження або приведеною інтенсивністю. Вона дорівнює середньому числу заявок, що надійшли у систему за середній час обслуговування заявки Із останнього співвідношення будемо мати розподіл ймовірностей станів СМО:

або

Використовуючи нормуючу умову, одержуємо:

Наведені формули називаються формулами Ерланга.

Алгоритм обчислення ймовірностей станів СМО. Обчислення ймовірностей станів здійснюється методом рекурсії. Спочатку, позначивши величини через і поклавши послідовно обчислюємо

Одночасно знаходимо суму

Використовуючи співвідношення одержуємо

Звідкіля одержуємо шукані значення

Знаючи всі імовірності станів можна знайти характеристики ефективності роботи СМО. Наведемо основні операційні характеристики обслуговування для розглядуваної n-канальної СМО з відмовами.

Операційні характеристики n-канальної СМО:

1. Імовірність відмови (імовірність втрати заявки)

де – імовірність того, що усі канали зайняті.

2. Відносна пропускна здатність системи (вона ж імовірність обслуговування , тобто імовірність того, що в момент надходження заявки на обслуговування хоча б один канал обслуговування буде вільним)

3. Абсолютна пропускна здатність системи (середнє число заявок, які обслуговуються СМО за одиницю часу)

4. Середнє число зайнятих каналів. Ця характеристика є найважливішою характеристикою СМО з відмовами (у даному випадку вона співпадає із середньою кількістю заявок, які знаходяться у системі). Позначимо її через Величину можна обчислити безпосередньо як математичне сподівання дискретної випадкової величини, яка приймає значення з імовірностями за формулою

Але можна також виразити середню кількість зайнятих каналів через абсолютну пропускну здатність А, яку ми вже маємо:

Дійсно, А є не що інше, як середня кількість заявок, обслужуваних в одиницю часу, а один зайнятий канал обслуговує у середньому за одиницю часу μ заявок. Тому середнє число зайнятих каналів буде дорівнювати відношенню А до :

5. Імовірність зайнятості каналу

6. Середній час простою каналу

7. Середній час повного завантаження системи (час перебування cистеми у стані S_n)

8. Середній час неповного завантаження системи (час, який протікає з моменту виходу системи із стану , до наступного моменту повернення її у цей стан)

Важливим параметром СМО є коефіцієнт використання систем, який визначається за формулою

,

де – інтенсивність, з якою робота надходить у систему, – час обслуговування. Час обслуговування дорівнює , де – максимальна інтенсивність (пропускної спроможності системи), з якою система може виконувати цю роботу. Для однолінійних систем параметр визначається як добуток інтенсивності надходження заявок у систему на середній час обслуговування:

У випадку багатолінійної системи (наприклад, коли у системі є каналів обслуговування) коефіцієнт використання системи має вигляд

Інтенсивність надходження роботи у систему іноді називається інтенсивністю навантаження системи.

При дослідженні СМО з відмовами іноді буває необхідно знайти таке число каналів обслуговування, при якому з заданою надійністю заявка була б обслужена. У такому разі необхідно проводити перерахунки параметрів СМО, збільшуючи кількість каналів на одиницю до тих пір, поки не одержимо задану надійність обслуговування заявки (імовірність обслуговування ).

Програма Smo_1. –СМО з відмовами

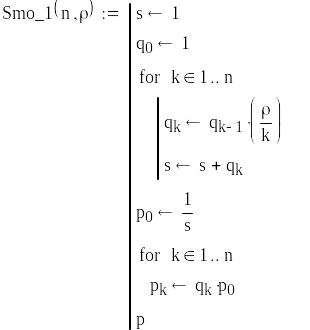
Вхідні дані:

n – кількість каналів обслуговування;

– інтенсивність вхідного потоку;

– інтенсивність обслуговування;

ρ – приведена інтенсивність .

Виклик програми:

Результат: p= < вектор-стовпець ймовірностей станів СМО>.

Приклад 2.1. Центр інформаційних технологій обладнаний трьома каналами зв’язку для прийому оперативної інформації, яка надходить від автопідприємств. Якщо в момент виходу на зв’язок якогось абонента усі канали зайняті, він змушений повторити свій виклик. Таким чином, роботу обчислювального центру можна розглядати як триканальну СМО з відмовами.

Інтенсивність вхідного потоку викликів = 0,8 за хв. Середня тривалість обслуговування заявки хв. (інтенсивність обслуговування заявки одним каналом =0,665 за хв.). Усі потоки подій – найпростіші. Таким чином дана СМО описується такими параметрами: n=3, λ= 0,8; 0,665.

Визначимо граничні (при ) імовірності станів СМО і основні операційні характеристики:

● імовірність зайнятості каналів (імовірність відмови в обслуговуванні абонента);

● відносну і абсолютну пропускну спроможності системи;

● середнє число зайнятих каналів;

● час простою системи;

● час повної зайнятості усіх каналів;

● cередній час неповного завантаження системи;

● коефіцієнт завантаження системи.

Розв'язання. Знаходження ймовірностей станів проводимо за програмою Smo_1.

Вхідні параметри СМО

n := 3 λ := 0.8 μ := 0.665 ρ := ρ =1.2