1.4. Моделювання вхідних і вихідних потоків у смо

Моделювання вхідних і вихідних потоків в системах масового обслуговування здійснюється за моделями процесів чистого народження і чистої загибелі, де процес народження моделює вхідний потік, процес загибелі – вихідний.

Модель народження. При заданій інтенсивності надходження заявок у систему обслуговування ймовірності її станів описуються системою диференціальних рівнянь Колмогорова

Для знаходження розв’язку системи рівнянь для процесу, який залежить від часу (нестаціонарного процесу), треба задати початкові умови:

Інтегруючи диференціальні рівняння з використанням початкової умови, одержуємо їх розв’язок:

Отже, ми приходимо до вже відомого нам розподілу Пуассона. Таким чином, процес чистого росту з постійною інтенсивністю приводить до пуассонівського процесу із середнім значенням і дисперсією, рівними Отже, кількість заявок, що надходять у систему масового обслуговування за час t, розподілена за законом Пуассона.

Модель загибелі. Аналогічно одержимо розподіл імовірностей числа подій у вихідному потоці, який моделюється процесом загибелі. У даній моделі припускається, що система починає функціонувати, коли в момент часу у ній є k заявок і не допускається надходження нових клієнтів. Клієнти після завершення обслуговування вибувають із системи з інтенсивністю клієнтів в одиницю часу.

Нехай імовірність того, що після часу t у системі зостанеться k клієнтів. Система диференціальних рівнянь у цьому випадку буде мати вигляд:

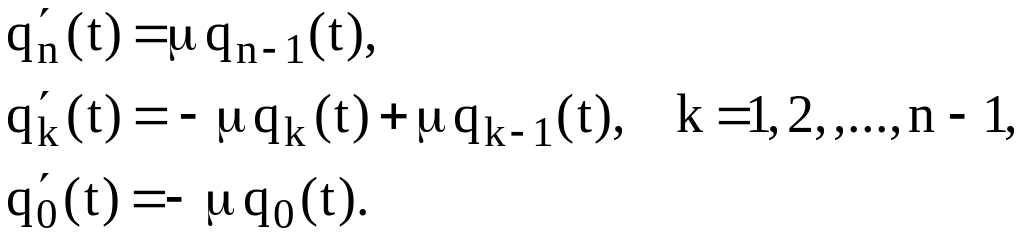
Ці рівняння мають розв’язок, який називається усікненим розподілом Пуассона:

У ряді випадків інтерес представляє ймовірність того, що після протікання t одиниць часу у системі залишиться k заявок на обслуговування. Тоді, якщо покласти, що у початковий момент часу число заявок, які знаходяться у системі, дорівнювало k, будемо мати

Звідкіля випливає, що кількість заявок, які залишаться у системі в момент часу буде визначатись формулами

У теорії масового обслуговування важливе значення має формула Літтла, яка визначає середню кількість заявок, що знаходяться у системі при умові, що система перебуває у стаціонарному режимі.

Вона визначається наступним чином. Нехай означає інтенсивність надходження заявок в систему у стаціонарному режимі, а середній час перебування заявок у системі. Тоді середня кількість заявок у системі дорівнює

Формула Літтла встановлює, що середня кількість заявок у системі дорівнює добутку інтенсивності надходження заявок у систему на середній час перебування заявки в системі.

Приклад 1.4. Надходження заявки на обслуговування у центр інформаційних технологій розподілено у часі за експоненціальним законом із середньою довжиною інтервалів між моментами надходжень у 0,2 години. При цьому інтенсивність потоку заявок у годину дорівнює надходжень.

Знайдемо:

a) оцінку об’єму пам’яті комп’ютера, яка потрібна для зберігання цієї інформації за місяць (30 днів);

b) частку часу, протягом якого оператор, який здійснює прийом заявок, виявиться незайнятим, тобто коли до оператора протягом робочого дня (8 годин) інформація не надходить;

c) імовірність того, що у кінці третього робочого дня у пам’ять комп’ютера буде введено 100 документів, якщо до кінця другого дня у пам’ять комп’ютера вже було введено 80 документів.

Розв’язання. Знаходимо

a) середня кількість заявок, яка надходить у центр інформаційних технологій за місяць (30 днів):

b) частка часу, протягом якого оператор комп’ютера виявиться незайнятим:

c) імовірність того, що у кінці третього робочого дня у пам’ять комп’ютера буде введено 100 документів, якщо до кінця другого дня у пам’ять комп’ютера вже було введено 80 документів. Ясно, що у цьому випадку протягом третього дня буде введено 20 документів, і ми одержуємо:

Контрольні запитання

1. Дати означення поняття ймовірнісного процесу.

2. Чи вірне твердження, що основою класифікації випадкових процесів є три характеристики: простір станів, індексуючий параметр (час) і статистичні залежності між випадковими значеннями процесу X(t), які відповідають різним значенням t.

3. Який аналітичний вигляд має марковська властивість випадкового процесу

4. Дати означення марковського випадкового процесу. Що таке марковський ланцюг.

5. Дати означення дискретного ланцюга Маркова. Який ланцюг Маркова називається однорідним.

6. Дати означення стаціонарного ймовірнісного процесу.

7. Дати означення незалежного ймовірнісного процесу. Який вигляд має математичний вираз незалежності значень випадкової послідовності.

8. Навести формулу для обчислення ймовірностей переходу ланцюга Маркова за n кроків.

9. Дати означення граничних імовірностей розподілу ланцюга Маркова.

10. Навести формулу для обчислення граничних імовірностей станів ланцюга Маркова.

11. Навести рівняння Колмогорова для перехідних імовірностей однорідного ланцюга Маркова.

12. Дати означення неперервного ланцюга Маркова. Як визначаються його ймовірності переходів.

13. Модель процесу народження і загибелі. Навести систему диференціально-різницевих рівнянь для ймовірностей станів цього процесу.

14. Як одержати диференціальні рівняння для ймовірностей станів процесу народження і загибелі за допомогою діаграми інтенсивностей переходів.

15. Дати означення процесу Пуассона. Навести формулу розподілу Пуассона.

16. Чому дорівнюють математичне сподівання і дисперсія розподілу Пуассона.

17. Дати означення експоненціального розподілу. Чому дорівнюють математичне сподівання і дисперсія цього розподілу Як пов’язані між собою розподіл Пуассона і експоненціальний розподіл.

Завдання для самостійної роботи: розв’язати наступні задачі.

1.1. Заданий однорідний ланцюг Маркова, діаграма станів якого має вигляд:

1-p

1

p q

1-q

а) знайти матрицю P перехідних ймовірностей;

б) знайти вектор p стаціонарного розподілу ймовірностей;

в) чому дорівнює середній час повернення процесу у стан 2;

г) при яких значеннях p і q виконується рівність p₁ = p₂ = p₃;

1.2. Розглянемо дискретний ланцюг Маркова з матрицею ймовірностей переходів

P = .

а) зобразити діаграму переходів ланцюга Маркова;

б) знайти вектор p стаціонарного розподілу ймовірностей;

в) знайти середній час повернення процесу у стан 2.

1.3. Розглянемо СМО, яка описується процесом народження і загибелі, у якій

а) зобразити діаграму інтенсивностей переходів СМО і записати диференціальні рівняння, які описують імовірності

б) знайти граничні ймовірності p_k при .

1.4. На автостоянку з числом місць N прибувають автомобілі, які утворюють пуассонівський потік з інтенсивністю , до тих пір, поки є вільні місця. Час стоянки автомобілів має пуассонівський розподіл ймовірностей.

а) вивести диференціальні рівняння для ймовірностей P_k(t) того, що рівно k місць виявляться зайнятими;

б) знайти граничний розподіл ймовірностей станів .

1.5. Протягом дуже малого проміжку часу u у систему обслуговування може надійти не більше однієї заявки. Імовірність надходження заявки пропорційна u з коефіцієнтом пропорційності 2. Треба визначити:

а) середню довжину проміжків часу між послідовними надходженнями заявок на обслуговування;

б) імовірність того, що протягом 0,5 одиниць часу не надійде жодної заявки;

в) імовірність того, що проміжок часу між послідовними надходженнями заявок на обслуговування дорівнюватиме одиниць часу;

г) імовірність того, що проміжок часу між послідовними надходженнями заявок на обслуговування виявиться рівним одиниць часу.

1.6. Клієнти надходять у систему обслуговування у відповідності з пуассонівським розподілом ймовірностей з середньою частотою λ=2 клієнти на годину. Визначити:

а) середнє число клієнтів, прибуваючих у систему протягом 8 годин;

б) імовірність того, що протягом 1 години в обслуговуючу систему надійде принаймні 1 клієнт.

Вказівка: Скористатись властивістю незалежності прирощень процесу Пуассона, згідно якій ймовірність настання k подій процесу на проміжку t залежить тільки від інтесивності потоку і довжини проміжку t:

1.7. Відвідувачі прибувають у ресторан у відповідності з пуассонівським розподілом з середньою частотою 20 відвідувачів на годину. Ресторан відкривається в 11 год. Треба обчислити:

а) імовірність того, що в 11,10 у ресторані виявиться 20 відвідувачів при умові, що 11,05 в ресторані було 18 відвідувачів;

б) імовірність того, що новий відвідувач прибуде у ресторан в інтервалі часу між 11,25 і 11,30, якщо відомо, що попередній відвідувач прибув у ресторан в 11,24.

Вказівка: Скористатись вказівкою до задачі 1.6.

1.8. Замовлені університетською бібліотекою книги надходять у відповідності з пуассонівським розподілом з середньою частотою 25 книг у день. На кожній полиці можна розмістити 100 книг. Треба обчислити:

а) середню кількість полиць, які виявляться заставленими книгами щомісяця;

б) імовірність того, що щомісячно для розміщення книг, які надходять, буде потрібно більше 10 секцій, якщо секція складається із 5 полиць.

Вказівка: Скористатись властивістю експоненціального розподілу ймовірностей, згідно якій умовний розподіл випадкової величини T дорівнює безумовному розподілу:

Відповіді до задач

1.1. б) в)

г)

1.2. б) в)

1.4. а)

б)

1.5. а) t = 0,5 ; б) ; в) ;

г) .

1.6. а) n= 16; б)

1.7. а) б)

1.8. а) б)