2.5. Замкнуті системи масового обслуговування

Математична модель. СМО називається замкнутою, якщо вона має обмежену кількість клієнтів. Розглянемо замкнуту СМО, яка має m каналів обслуговування (сервісів), які обслуговують групу із n клієнтів (m < n). Інтенсивність потоку заявок на обслуговування від кожного клієнта дорівнює . Якщо клієнт, подав заявку на обслуговування і у цей момент є вільний канал, він приступає до обслуговування клієнта. На це витрачається час де – інтенсивність потоку обслуговувань. Якщо в момент прибуття клієнта усі канали зайняті, клієнт стає у чергу і чекає, поки не звільниться який-небудь канал.

Припускається, що проміжки часу між моментами надходженнями клієнтів у систему обслуговування і тривалості обслуговування розподілені за експоненціальними законами відповідно з параметрами λ і μ, тобто вхідний і вихідний потоки є пуассонівськими.

Треба визначити імовірності станів даної системи та її операційні характеристики.

Система, яка має m каналів обслуговування і джерелом заявок є n клієнтів, має стани, які нумеруються за кількістю поданих заявок k. Очевидно, що вона може знаходитись у станах S₀, S₁, ..., S_n. Параметри СМО:

Діаграма інтенсивностей переходів замкнутої СМО показана на рис. 2.4.

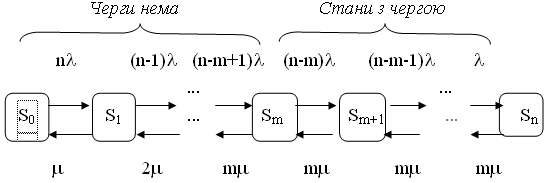
Рис. 2.4. Діаграма інтенсивностей переходів системи

Із діаграми видно, що із стану у стан систему переводить потік заявок від усіх клієнтів, його інтенсивність дорівнює Із стану у стан систему переводить потік заявок від клієнтів (один клієнт вже обслуговується) і т. д. Інтенсивності потоків подій, які переводять систему справа уліво залежать від кількості заявок, які обслуговуються у даний момент і дорівнюють . Застосовуючи методику виведення рівнянь для ймовірностей станів системи у стаціонарному режимі при одержимо систему різницевих алгебраїчних рівнянь

(2.13)

Із цієї системи знаходимо граничні імовірності станів даної СМО. Вводячи приведену інтенсивність обслуговування , одержимо такі формули:

(2.14)

де

.

, (2.15)

Із цих формул можна одержати рекурентні формули для ймовірностей станів у вигляді:

(2.16)

У ці формули входить невідоме значення p₀. Воно обчислюється за наступним алгоритмом. Позначимо у наведених формулах і покладемо спочатку . Обчислимо q_k (k=1,...,n) за цими формулами, а також суму

Використовуючи умову нормування ймовірностей, запишемо

.

Звідкіля знаходимо величину . Помноживши тепер на , знаходимо шукані величини

.

Операційні характеристики СМО:

Операційні характеристики замкнутої СМО будуть відмінні від тих, які ми застосовували раніш для СМО з необмеженою кількістю джерел заявок. Так роль абсолютної пропускної спроможності у даному випадку буде відігравати середня кількість клієнтів, що обслуговується в одинцю часу. Відносна пропускна здатність у даному випадку не обчислюється, оскільки кожна заявка, у кінці кінців, буде обслужена. Отже будемо мати такі характеристики:

1. Середнє число зайнятих каналів обслуговування

.

2. Середнє число незайнятих каналів обслуговування

або

3. Середнє кількість заявок, які знаходяться на обслуговуванні

4. Середня кількість заявок у системі (заявок, які знаходяться на обслуговуванні і у черзі)

або .

5. Середнє число заявок у черзі

Між вказаними величинами існують співвідношення

6. Середнє число заявок, які знаходяться поза системою

або

7. Абсолютна пропускна здатність (середнє число заявок, які обслуговуються в одиницю часу

.

8. Середній час знаходження заявки у системі:

.

Ця формула випливає із співвідношення

.

де де – ефективна інтенсивність вхідного потоку, яка одержується, якщо врахувати, що у стаціонарному режимі параметр потоку дорівнює не , а

9. Середній час чекання заявки у черзі

або

Він одержується із рівності

.

де .

Із формули для можна одержати також середню кількість заявок у вигляді

.

10. Коефіцієнт простою заявок у черзі

11. Коефіцієнт простою каналу:

12 .Імовірність того, що заявка у будь-який момент часу буде знаходитись поза системою обслуговування

або

де – середня кількість заявок, які знаходяться у системі, – середній час знаходження заявки поза системою.

Величину називають також коефіцієнтом оперативного використання каналів обслуговування.

Програма Smo_4. Замкнута СМО

Вхідні дані:

n – кількість каналів обслуговування;

m – кількість місць у черзі;

– інтенсивність вхідного потоку;

– інтенсивність обслуговування;

ρ – приведена інтенсивність (ρ=λ/μ).

Виклик програми:

Результат: p = < вектор-стовпець ймовірностей станів СМО>.

Приклад 2.7. Обслуговування 8 автомобілів автотранспортної фірми доручено 2 механікам. Приведена інтенсивність обслуговування Отже, маємо замкнуту СМО з такими параметрами:

n=8, m=2,  = 0,2.

Розв'язання. Обчислення ймовірностей станів СМО здійснюються за програмою Smo_4. Результати обчислень імовірностей станів і її функціональні характеристики подані у таблицях 2.5 і 2.6..

Алгоритм у Mathcad

Вхідні параметри

Результати програми – вектор ймовірностей станів СМО

p:=Smo_4(n, m, ρ)

Операційні характеристики СМО:

1. Середня кількість зайнятих механіків

2. Абсолютна пропускна здатність системи (середня кількість автомобілів, які обслуговуються в одиницю часу

3. Середня кількість не зайнятих механіків

4. Середня кількість автомобілів у системі обслуговування (автомобілів, які знаходяться на обслуговуванні і у черзі)

5. Середня кількість автомобілів у черзі на обслуговування

6. Середня кількість працюючих автомобілів (кількість автомобілів поза системою обслуговування)

7. Середній час чекання автомобілів у черзі

8. Середній час знаходження автомобілів у системі обслуговування (час обслуговування + час у черзі)

9. Коефіцієнти простою автомобілів і механіків

Таблиця 2.5. Імовірності станів СМО p_k для n = 8, m =2,  =02.

Число непрацюючих автомобілів k	0	1	2	3	4	5	6	7	8
Число автомобілів у черзі	0	0	0	1	2	3	4	5	6
Число незайнятих механіків	2	1	0	0	0	0	0	0	0
І мовірності станів pk	0,204	0,33	0,23	0,14	0,07	0,03	0,01	0,0	0,0

Таблиця 2.6. Операційні характеристики СМО

Характеристика	Позначення	Значення
Число робітників Число станків Число станків на 1 робітника Абсолютна пропускна здатність Середнє число зайнятих робітників Середнє число непрацюючих станків Середня кількість станків у черзі Коефіцієнт простою робітників Коефіцієнт простою станків	m n – А	2 8 4 5,07 1,27 1,67 0,4 0,37 0,05

Приклад 2.8. Навантажувач обслуговує 3 автомобіля (n = 3). Кожний автомобіль підходить під навантаження в середньому 2 рази на годину. Навантаження автомобіля займає в середньому 10 хв. Визначимо характеристики замкнутої одноканальної СМО: абсолютну пропускну здатність СМО, середню зайнятість та простій навантажувача, середню кількість автомобілів у черзі, середню кількість автомобілів у системі обслуговування – під навантаженням і у черзі, середнє число автомобілів поза системою обслуговування, коефіцієнт простою автомобілів, коефіцієнт простою навантажувача.

Розв'язання. Імовірності станів СМО знайдемо по програмі Smo_4.

Вхідні параметри

Одержуємо такі імовірності станів СМО:

p:=Smo_4(n, m, ρ)

p^T = (0.346 0.346 0.231 0.077)

Операційні характеристики СМО:

1. Середня зайнятість навантажувача

або

2. Середнє число не зайнятих навантажувачів

3. Середнє число автомобілів у системі обслуговування (автомобілів, які знаходяться на обслуговуванні і у черзі)

4.Середнє число автомобілів у черзі на обслуговування

5. Середнє число працюючих автомобілів

6. Абсолютна пропускна здатність системи (середнє число автомобілів, які обслуговуються в одиницю часу

7. Середній час чекання автомобіля у черзі

8. Середній час знаходження автомобіля у системі

9. Коефіцієнт простою автомобілів

10. Коефіцієнт простою навантажувача

Приклад 2.9. Таксомоторна фірма, яка здійснює обслуговування клієнтів деякого району, має 10 автомобілів. Протягом робочої зміни автомобілі і водії за певними технічними причинами проходять відповідне обслуговування. Середня кількість цих обслуговувань у день дорівнює . Середня тривалість одного обслуговування складає хв.

Визначимо основні операційні характеристики даної СМО.

Розв’язання. Оскільки у даній системі загальна кількість джерел навантаження обмежена (кількість водіїв і автомобілів дорівнює 10) і черга на обслуговування відсутня, то процес роботи таксофірми описується розглянутою моделлю СМО.

Алгоритм у Mathcad

Вхідні параметри моделі

_{Імовірностей станів}

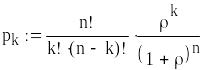
Операційні характеристики СМО:

_{1. Середнє число зайнятих каналів}

2. Відносна і абсолютна пропускні спроможності

3. Коефіцієнт простою автомобілів

Завдання для лабораторної роботи №5

У комп’ютерному класі вузу є комп’ютерів, за якими працюють студенти. Заняття зі студентами проводять викладачів, які підходять до студентів з метою контролю ходу виконання ними роботи або за зверненням студентів для консультацій. Інтенсивність потоку заявок від одного студента до викладачів за час занять дорівнює разів. Час обслуговування одного студента дорівнює Таким чином, робота комп’ютерного класу описується моделлю замкнутої СМО з джерелами навантаження і обслуговуючими каналами.

Визначити:

 функціональні характеристики даної СМО.

 яким повинен бути час обслуговування студентів, щоб час чекання студентом підходу до нього викладача не перевищувала 5 хв.

Таблиця 2.7

Вхідні дані по варіантах завдань

Номер варіанту	n				Номер варіанту	n
1	20	2	2	2	16	20	2	2	2
2	22	1	3	3	17	15	2	4	3
3	23	2	2	3	18	20	1	2	4
4	25	2	3	2	19	30	2	2	2
5	20	5	2	2	20	25	2	3	2
6	15	1	2	4	21	30	3	3	2
7	20	2	2	3	22	28	2	2	3
8	28	2	2	2	23	25	2	2	2
9	26	2	2	4	24	24	2	2	2
10	27	2	3	3	25	22	2	3	2
11	15	1	3	4	26	20	2	3	4
12	20	2	2	3	27	30	2	2	2
13	28	2	2	2	28	25	3	2	2
14	26	5	2	4	29	30	2	2	2
15	27	1	2	3	30	28	2	3	3