2.4. Смо з обмеженим часом чекання

Математична модель. Розглянемо СМО з чеканням, обмеженим не довжиною черги, а часом чекання початку обслуговування. У таких СМО заявки, що надійшли у систему, деякий час чекають обслуговування і по закінченні його покидають систему.

Припустимо, що є n-канальна СМО з чеканням (з чергою), у якій кількість місць у черзі не обмежене, але час чекання заявки у черзі обмежений деяким випадковим терміном з середнім значенням . Величина має експоненціальний закон розподілу з параметром . Параметр має смисл трактувати як інтенсивність уходу із черги необслужених заявок.

Позначимо також через інтенсивність вхідного потоку заявок, а через інтенсивність обслуговування заявки одним каналом. Як і раніше, є середній час між сусідніми заявками, які надходять у систему обслуговування, а середня тривалість обслуговування заявки.

Знайдемо ймовірності станів розглядуваної СМО. Будемо нумерувати стани системи за числом заявок, які знаходяться у системі, як ті, що обслуговуються, так і ті, що стоять у черзі:

– система вільна;

– зайнято k каналів (k = 1, ..., n);

– n каналів зайнято, обслуговується n заявок і заявок знаходяться у черзі, r=1,..., .

Діаграма інтенсивностей переходів СМО зображена на рисунку.

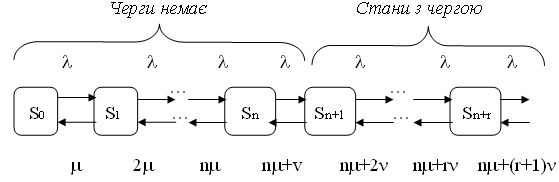
Рис. 2.3. Діаграма інтенсивностей переходів системи

Із діаграми видно, що для станів з чергою у стрілок, які йдуть справа наліво, стоїть сумарна інтенсивність потоку обслуговувань усіх n каналів n і відповідної інтенсивності потоку виходів із черги. Якщо у черзі є r заявок, то сумарна інтенсивність потоку виходів буде r.

Параметри СМО будуть такими: кількість каналів обслуговування n, інтенсивність вхідного потоку , інтенсивність обслуговування

Маємо схему народження і загибелі. Застосовуючи загальні вирази для граничних імовірностей станів і вводячи позначення =/, =/, одержимо:

(2.11)

(2.12)

Відмітимо деякі особливості розглядуваної СМО. Якщо довжина черги не обмежена ніяким числом і заявки “терплячі” (не виходять з черги), то стаціонарний режим існує тільки у випадку  < 1, що фізично відповідає відсутності нескінченого зростання черги при t . Для СМО з “нетерплячими” заявками, які рано чи пізно виходять із черги (і таким чином черга у системі обмежена), усталений режим обслуговування при t  досягається завжди, незалежно від величини приведеної інтенсивності .

Для СМО з обмеженим часом чекання поняття “імовірність відмови” не має смислу – кожна заявка стає у чергу, але може і не дочекатись обслуговування, пішовши із СМО раніше часу.

Операційні характеристики СМО:

1. Абсолютна пропускна здатність СМО. Вона обчислюється наступним чином. Очевидно, що обслужені будуть усі заявки, крім тих, які уйдуть із черги достроково. На кожну заявку, яка знаходиться у черзі діє “потік уходів” з інтенсивністю . Значить, із середньої кількості заявок у черзі в середньому буде уходити, не дочекавшись обслуговування, заявок в одиницю часу. Всього в одиницю часу в середньому буде обслужено заявок. Таким чином, абсолютна пропускна здатність дорівнює

.

Звідсіля визначається відносна пропускна здатність СМО

2. Середня кількість зайнятих каналів

.

3. Середнє число заявок у черзі. Знайдемо його як математичне сподівання кількості заявок у черзі R:

.

4. Середнє число заявок, які покидають чергу

де  – інтенсивність потоку виходів заявок із черги.

5. Середній час чекання у черзі

6. Середній час перебування заявки у системі

Програма Smo_3. СМО з обмеженим часом чекання

Програма визначення ймовірностей станів.

Вхідні дані:

кількість каналів обслуговування;

інтенсивність вхідного потоку;

інтенсивність обслуговування;

приведена інтенсивність обслуговування

інтенсивність виходу заявок із черги;

приведена інтенсивність потоку виходу заявок із черги

Виклик програми:

Результати:

p = < вектор-стовпець ймовірностей станів СМО>

r = <максимальна кількість заявок у системі>.

Приклад 2.6. При внесенні платежів клієнтами у каси банку вони можуть обслуговуватись у одній із чотирьох кас. Середній час прийому платежів складає Інтенсивність потоку клієнтів у банк =0,4 у хвилину. Якщо клієнт, який хоче внести платіж, застає усі каси зайнятими, він може деякий час чекати своєї черги. Середній час чекання Клієнт, який очікує у черзі більше 20 хвилин, покидає чергу.

Визначимо ймовірності станів СМО та її операційні характеристики.

Розв'язання. За умовою задачі ми маємо СМО з обмеженим часом чекання. Розрахунки ймовірностей станів такої системи проводимо за програмою Smo_3.