2.3.2. Смо з n каналами обслуговування і необмеженою чергою

Математична модель. n-канальна СМО з необмеженою чергою визначається такими параметри вхідного і вихідного потоків:

Умова існування стаціонарного режиму – = / n < 1. При  > 1 такого режиму не існує і черга при зростає до нескінченності.

Імовірність станів цієї СМО можна одержати із формул для СМО з чергою при Будемо мати:

p_k= (2.8)

Враховуючи нормуючу умову ймовірностей, знаходимо

(2.9)

Друга сума при являє собою геометричну прогресію і дорівнює:

Тепер вираз для буде мати вигляд:

. (2.10)

Якщо , то геометрична прогресія є розбіжною і значення прямують до нуля, а черга до нескінченності. У цьому випадку СМО не справляється з обслуговуванням.

Операційні характеристики СМО:

1. Середня кількість зайнятих каналів (середня кількість обслужуваних заявок)

3. Середня кількість заявок у черзі

4. Середня кількість заявок у системі.

де

5. Середній час чекання заявки у черзі.

6. Середній час перебування заявки у системі

.

де – час обслуговування однієї заявки.

7. Імовірність наявності черги

8. Імовірність зайнятості каналів обслуговування

9. Імовірність чекання заявки у черзі

Програма Smo_2.2. СМО із нескінченою чергою

Вхідні дані:

n – кількість каналів обслуговування;

m –максимально можлива довжина черги;

– інтенсивність вхідного потоку;

– інтенсивність обслуговування;

ρ – приведена інтенсивність .

Виклик програми:

Результат: p= < вектор-стовпець ймовірностей станів СМО>.

Приклад 2.5. На вантажній автостанції (ВАС) здійснюється навантажування контейнерів на автомобілі за допомогою автонавантажувачів. Інтенсивність потоку автомобілів, що прибувають на ВАС, дорівнює автомобілів у хвилину. Середній час навантажування автомобіля дорівнює хв. Автомобіль, що прибуває під навантажування і застає всі автонавантажувачі зайнятими, стає в чергу і чекає свого обслуговування.

Визначити характеристики ефективності вантажних робіт на ВАС.

Алгоритм у Mathcad

Вхідні параметри СМО:

1. Імовірності станів системи:

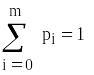
2. Середня кількість зайнятих навантажувачів

3. Середня довжина черги

4. Середня кількість автомобілів на ВАС

5. Середній час чекання у черзі

5. Середній час перебування автомобіля на ВАС

7. Імовірність зайнятості системи

8. _{Імовірність чекання автомобіля у черзі}

_{Завдання для лабораторної роботи №3}

Регіональна виборча комісія здійснює моніторинг ходу вборів. Офіс комісії має комп’ютерів для прийому SMS-повідомлень. Потік SMS-повідомлень утворює пуассонівський процес з інтенсивністю Середній час прийому повідомлень складає хв. Повідомлення, які надійшли на комп’ютери комісії, зберігаються у їх пам’яті, утворюючи чергу. Черга практично не обмежена, так що робота комп’ютерної системи описується моделлю СМО з необмеженою чергою.

Визначити функціональні характеристики даної СМО. Визначити також, яким повинен бути час обробки SMS-повідомлень, щоб черга не перевищувала 10 повідомлень.

Таблиця 2.3

Вхідні дані по варіантах завдань

Номер варіанту	n			Номер варіанту	n
1	1	3	0,30	16	1	2	0,47
2	4	4	0,20	17	4	5	0,19
3	1	2	0,45	18	2	4	0,24
4	4	5	0,18	19	1	2	0,46
5	1	3	0,30	20	2	3	0,32
6	3	4	0,22	21	3	2	0,42
7	2	3	0,30	22	1	3	0,90
8	1	4	0,24	23	2	4	0,24
9	4	4	0,24	24	3	3	0,33
10	1	1	0,90	25	2	5	0,18
11	2	4	0,24	26	3	3	0,31
12	3	5	0,18	27	2	3	0,30
13	4	4	0,21	28	1	2	0,48
14	3	4	0,24	29	2	3	0,28
15	3	5	0,19	30	3	4	0,23