Імовірності станів системи:

p := Smo_2(n, ρ)

p^T = (0.008 0.032 0.064 0.128 0.256 0.512)

Операційні характеристики СМО:

1. Імовірність відмови

2. Відносна і абсолютна пропускні спроможності

3. Середня кількість зайнятих каналів

4. Середня довжина черги

5. Середня кількість автомобілів на СТО

6. Середній час чекання у черзі

7. Середній час перебування автомобіля на СТО

8. _{Імовірність зайнятості каналів обслуговування}

9. Імовірність наявності черги

_{10. Коефіцієнт зайнятості каналів обслуговування}

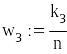
_{Завдання для лабораторної роботи №2}

У банку є кас для обслуговування клієнтів. Клієнти прибувають у банк у відповідності з пуассонівським розподілом імовірностей з інтенсивністю клієнтів на годину. Хол для чекання обслуговування вміщує не більше клієнтів. Тривалість прийому обслуговування підкоряється експоненціальному закону розподілу ймовірностей із середнім значенням клієнтів на годину. Якщо прибувший клієнт застає зайнятими усі каси і усі місця для чекання, він вимушений повторно повертатись до кас банку.

Треба визначити функціональні характеристики системи обслуговування у банку як СМО з чергою, обмеженою кількістю місць для чекання.

Визначити, яка повинна бути інтенсивність обслуговування клієнтів, щоб імовірність відмови клієнту у обслуговуванні не перевищувала 0,1.

Таблиця 2.2

Вхідні дані по варіантах завдань

Номер варіанту	n	m			Номер варіанту	n	m
1	3	10	35	15	16	2	15	40	22
2	4	18	45	12	17	4	18	42	12
3	3	15	40	10	18	2	12	42	25
4	4	10	35	8	19	3	10	45	18
5	3	15	30	6	20	2	8	38	20
6	5	15	45	6	21	3	10	38	12
7	2	12	30	12	22	3	15	40	14
8	3	10	40	10	23	2	12	45	24
9	4	15	45	7	24	3	15	38	14
10	3	10	48	18	25	2	10	50	26
11	2	15	45	26	26	3	12	35	12
12	3	12	40	18	27	2	15	38	20
13	4	15	42	12	28	3	12	32	12
14	3	18	45	20	29	2	15	30	18
15	3	15	46	18	30	3	12	42	14