37. Проблемы интерпретации данных. Потолочный эффект

Роль и значение интерпретации велики. Правильная интерпретация позволяет сопоставлять научные концепции с описываемыми ими фрагментами реального мира; порождать практические рекомендации; предлагать оптимальные способы действия и т.п. Обычно интерпретация основывается на исходных данных. Исследователи выделяют два таких уровня исходных данных: содержательный и формальный. Как правило, исходными данными называют данные содержательного уровня.

Содержательный уровень данных — это совокупность опытных (эмпирических) объектов (допустим, участников группы), рассматриваемых вместе с интересующими исследователя отношениями между ними (например, их межличностными отношениями). Эмпирическая система с отношениями — это модель реальности, в которой каждый объект является носителем интересующих нас явлений, отношений. От других отношений этих объектов мы абстрагируемся, т.е. не учитываем их, считая несущественными.

Формальный уровень данных — это совокупность результатов измерений. В процессе измерения каждому представленному в опыте объекту приписывается некоторый формальный символ (чаще математический). Отображение эмпирической системы в математическую происходит в процессе измерения. Обычно в этом процессе мы присваиваем числа определенным психическим свойствам и их отношениям.

Используя тот или иной математический метод, мы предполагаем, что элементы применяемых при измерении математических систем позволяют реализовать ряд условий.

1. Отношения между элементами математической системы (например, числами) отражают соответствующие отношения между эмпирическими объектами (допустим, ценностными предпочтениями обследуемых). Например, применяя порядковую шкалу для измерения удовлетворенности межличностными отношениями, мы предполагаем, что отношения больше/меньше между ответами обследуемых (т.е. между приписываемыми им числами) соответствуют аналогичным отношениям между реальными “удовлетворенностями” тех же обследуемых.

2. Определенные отношения между элементами математической системы отражают соответствующие опытные (эмпирические) отношения даже тогда, когда намеренное моделирование последних в процессе измерения не производилось. Подобная уверенность обычно базируется на содержательных гипотезах, опирающихся на интуицию исследователя.

3. Интересующее исследователя явление отражается в математической модели, для идентификации (распознавания) параметров которой предназначен используемый метод. Так, например, применяя анализ линейных корреляций, мы предполагаем, что между значениями зависимой и независимой переменных существуют линейные связи.

Возможность идентификации параметров модели, определяемой математическим методом, также опирается на ряд предположений: о характере распределения рассматриваемых признаков (например, требование нормальности распределения значений параметра); о механизмах формирования исходных данных (например, предположение о наличии среди обследуемых некоторого “идеального” объекта, степени сходства с которым определяют значимость ранжируемого объекта) и т.п. Нередко подобные предположения не подвергаются практической проверке, а исследователю бывает недостаточно интуитивной оценки их справедливости.

В процессе интерпретации первичных данных необходимо применять два принципа интерпретации:

1) принцип согласованной интерпретации. Согласно этому принципу, интерпретацию результатов применения математического метода необходимо согласовывать с интерпретацией исходных данных;

2) принцип дополнения формализма. В соответствии с указанным принципом, если содержательные соображения не отразились в интерпретации исходных данных, то необходимо их отразить при интерпретации результатов применения метода.

Проблемы интерпретации данных:

- Проблема потолочного эффекта (ceiling and floor effects)

- Проблема возврата к средней величине (регрессия к среднему – regression to mean)

Проблема потолочного эффекта:

Заключается в трудности интерпретации данных, которые близки к экстремальным значениям измерительной шкалы.

Проблема потолочного эффекта:

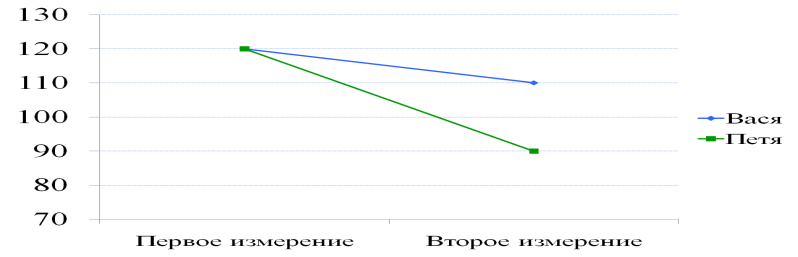
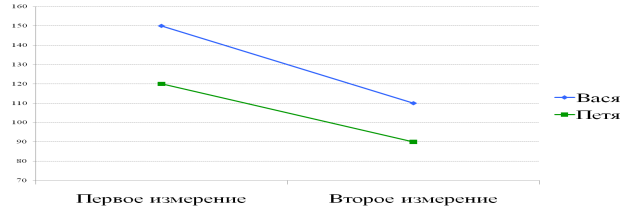
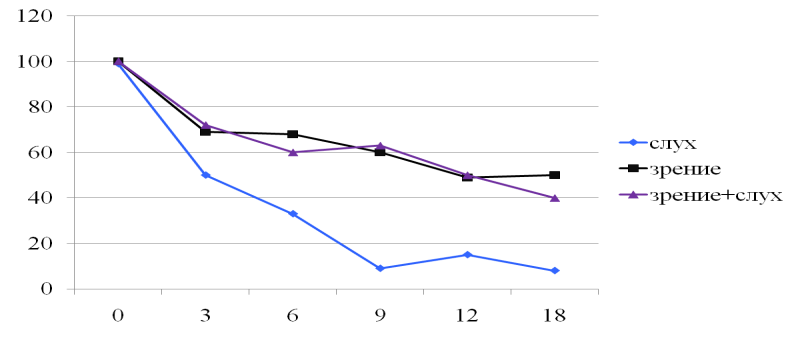
Пути решения проблемы:

1) провести пилотажные исследования (претесты)

2) не учитывать данные, которые близки к пределу значения переменной