
- •1.Цели и задачи освоения дисциплины
- •2. Место дисциплины в структуре ооп
- •3. Требования к результатам освоения дисциплины
- •Часть I по разделу 1
- •«Моделирование национального рыночного хозяйства на макроуровне»
- •Методические указания к выполнению части ӏ для курсового задания по разделу 1 "Моделирование национального рыночного хозяйства на макроуровне"
- •Часть II по разделу 2
- •Методические указания по выполнению части 2 для курсового задания по разделу 2 «Модели развития отдельных секторов и сфер национальной экономики»
- •Образец титульного листа курсового проекта
- •Список литературы Основная литература
- •Дополнительная литература
Методические указания к выполнению части ӏ для курсового задания по разделу 1 "Моделирование национального рыночного хозяйства на макроуровне"
Исходные данные для модели Солоу:
- фактор шкалы А = З
- доли материальных затрат в совокупном продукте а = 0,2
- коэффициент эластичности выпуска по затратам фондов α = 0,60
- доля инвестирования в конечном продукте р = 0,50
- доля износа фондов μ = 0,15
- темп роста трудовых ресурсов ν = 0,02
В стационарном режиме:
фондоёмкость
труда k0
=(
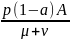
 = 132,38
= 132,38
производительность труда y0 = A*(k0)α = 56,26
удельное непроизводственное потребление с0 = (1-а)(1-ρ)у0 = 22,50
Оптимальная доля инвестирования позволяет обеспечить максимально возможный при заданной технологии уровень удельного непроизводственного потребления в стационарном режиме.
Если технология описывается производственной функцией Кобба--Дугласа, то оптимальная доля инвестирования равна эластичности выпуска по затратам фондов
ρ *=α=0,60
Это означает — 60% стоимости конечного продукта должно инвестироваться. 2.Исходные данные для модели «Затраты - выпуск»:
-матрица прямых затрат продукции:
А=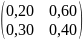
-вектор конечного
выпуска: Y =

1) Проверим объект на продуктивность.
В матрице прямых затрат продукции нет нулевых элементов, следовательно она неразложима. Применим признаки проверки на продуктивность.
0,20+0,60<1 0,30+0,40<1
Следовательно, объект продуктивен.
2) Найдем матрицу валовых удельных выпусков согласно алгоритму:
А →Е-А → (Е-А) -1
C=E-A=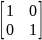 -
-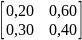 =
=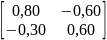
det С = det(E — A) =0,80 •0,60 - (-0 60) • (-0,30) = 0,48-0,18 =0,30
(E-A)-1=C-1= =
=
(E-A)-1=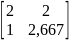
3) Найдем валовые выпуски отраслей:
Х =(Е-А)-1
•Y=
•
=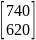
4) Рассчитаем межотраслевые потоки:
Х11 = а11 • X1 = 0,20 • 740 = 148
Х12 = а12 • Х2 = 0,60 • 620 = 372
X21 = а21 • Х 1 = 0,30 • 740 = 222
X22 = а22 • Х 2 = 0,40 • 620 = 248
5) Составим таблицу межотраслевого баланса
Производящие отрасли |
Распределение по потребляющим отраслям |
Объем конечного потребления |
Объем валового выпуска |
|
1 |
2 |
|||
1 |
148 |
372 |
220 |
740 |
2 |
222 |
248 |
150 |
620 |
3.Исходные данные для расчета по модели Неймана. матрица затрат продукции:
A=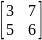
матрица выпуска продукции:
B=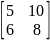
вектор запаса продукции на начало моделирования:
S=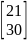
вектор цен на продукцию:
Р = (4,7)
1) Введем вектор
интенсивностей применения технологий:
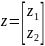 2)
Составим модель задачи:
2)
Составим модель задачи:
F = PBZ →max F = P1 (b11Z1+ b12Z2)+ P2(b21Z1 + b22Z2 ) → max
AZ ≤ S a11Z1 + а 12Z2≤ S1
Z ≥ 0 a21Z1, + a22Z 2≤ S2
Z1,Z2 ≥ 0
62 Z1 + 96Z2→max
3Z1 + 7Z2 ≤ 21
5 Z1 +6Z2 ≤ 30
Z1,Z2 ≥ 0
Далее, задача линейного программирования решается графически.
