
- •1. Кинематика поступательного движения
- •2. Равномерное прямолинейное движение
- •3. Равнопеременное прямолинейное движение
- •4. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорение.
- •5. Криволинейное движение. Тангенциальное и полное ускорение.
- •6. Равнопеременное движение по окружности. Угловые пути, скорость, ускорение, период, частота.
- •7. Законы ньютона
- •8. Импульс. Закон сохранения импульса тела.
- •9. Закон сохранения импульса при взаимодействии двух тел (из 3-его закона Ньютона).
- •10. Закон сохранения импульса при абсолютно упругом и абсолютно неупругом ударе.
- •11. Закон всемирного тяготения. Работа сил тяготения. Потенциальная энергия гравитационного поля.
- •12. Закон Гука. Работа силы упругости. Энергия сжатой пружины.
- •13. Результирующая сила. Кинетическая энергия. Работа результирующей силы.
- •16.Динамика вращательного движения. Момент инерции.
- •17. Теорема Штейнера
- •18. Момент силы. Основной закон динамики вращательного движения.
- •19. Работа при вращательном движении тела
- •20. Кинетическая энергия при вращательном движении
- •21. Момент импульса. Закон сохранения момента импульса.
1. Кинематика поступательного движения
Кинематика - раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих.
Материальная точка – тело, размерами которого можно принебреч в данных условиях.
Траектория – линия, вдоль которой двигается тело.
Прежде чем решать любую задачу механики необходимо выбрать систему отсчёта.
Система отсчёта – тело отсчёта (начало отсчёта), система координат связанных с ним, с указанием направления, масштаба и времени отсчёта.
Путь – длина участка траектории материальной точки, пройденного ею за определённое время.
Расстояние – длина прямой, соединяющей начальную и конечную точки.
Вектор перемещения – направленный отрезок, соединяющий начальную и конечную точки и указывающий направление движение.
Для произвольной точки в пространстве, радиус-вектор – это вектор, ведущий из начала координат в эту точку. На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.
2. Равномерное прямолинейное движение
Равномерное прямолинейное движение - это механическое движение, при котором тело за любые равные промежутки времени проходит равные расстояния, равные пути, равные перемещения.
|
-скорость прямолинейного движения.
|
Скорость показывает, какое перемещение совершает тело за единицу времени, двигаясь прямолинейно и равномерно.
|
- проекция вектора перемещения и проекция вектора скорости |
|
- Уравнение равномерного прямолинейного движения. Решение основной задачи механики для прямолинейного равномерного движения.
|
Графики скорости:

3. Равнопеременное прямолинейное движение
Равнопеременное прямолинейное движение – такое движение, при котором ускорение есть величина постоянная (a=const), а траектория есть прямая линия. Направление вектора ускорения при этом может совпадать с направлением начальной скорости движения или же быть направлено в противоположную сторону.
Ускорение – Изменение скорости в единицу времени.

Равноускоренное – ускорение постоянное, скорость увеличивается.
Равнозамедленное – ускорение постоянное, скорость уменьшается.
 - скорость для равноускоренного
движения.
- скорость для равноускоренного
движения.
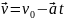 – скорость для равнозамедленного
движения.
– скорость для равнозамедленного
движения.

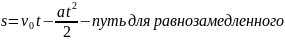
Ускорение – тангенс угла наклона касательной к оси времени к графику V(t) для данного момента времени.
4. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорение.
Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.
Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции Vx и Vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам :
|
|
|
|
Частным случаем
криволинейного движения – является
движение по окружности. Если за любые
равные промежутки времени радиус-вектор
тела поворачивается на одинаковые углы,
а линейная скорость тела по модулю не
изменяется (т. е. если |v0|=|v|), движение
тела по окружности называют равномерным.
Движение по окружности, даже равномерное,
всегда есть движение ускоренное: модуль
скорости все время направлен по
касательной к траектории, постоянно
меняет направление, поэтому движение
по окружности всегда происходит с
центростремительным ускорением
![]() где r – радиус окружности.
где r – радиус окружности.

Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.
Центростремительное ускорение меняет скорость только по направлению, но не меняет по величине. Вектор центростремительного ускорения перпендикулярен вектору скорости.
Используя связь между угловой и линейной скоростями, получим:
![]()


