
- •Тема №1. Линейные пространства Теоретические вопросы темы
- •Линейные пространства
- •Линейная зависимость систем векторов
- •Базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений (ослау)
- •Формулы перехода от базиса к базису. Формулы преобразования координат при переходе от базиса к базису
- •Подпространства линейных пространств. Сумма и пересечение подпространств
- •Скалярное произведение векторов, евклидовы пространства
- •Процесс ортогонализации Шмидта
- •Дополнение системы векторов до ортогонального базиса
- •Тема №2. Линейные операторы Теоретические вопросы темы
- •Линейные операторы, их структуры
- •Структура линейного оператора
- •Матрицы линейного оператора в разных базисах
- •Собственные числа и собственные векторы линейного оператора
- •Сопряженные линейные операторы
- •Теорема Фредгольма, ее применение к исследованию слау
- •Ортогональные матрицы и ортогональные операторы
- •Приведение матрицы линейного оператора к диагональному виду
- •Тема №3. Квадратичные формы Теоретические вопросы темы
- •Квадратичные формы, их канонический вид. Метод Лагранжа приведения квадратичной формы к каноническому виду
- •Метод ортогональных преобразований приведения квадратичной формы к каноническому виду. Знакоопределенные и знакопеременные квадратичные формы
- •Библиографический список
Сопряженные линейные операторы
Пусть V
– евклидово
пространство с ортонормированным
базисом
.
Линейный оператор
![]() называется сопряженным
к оператору
,
если для любых
выполняется равенство:
называется сопряженным
к оператору
,
если для любых
выполняется равенство:
![]() .
.
Любому линейному
оператору
соответствует единственный сопряженный
оператор
![]() ,
причем его матрицей
,
причем его матрицей
![]() является матрица, транспонированная
к матрице
является матрица, транспонированная
к матрице
![]() линейного оператора
.
линейного оператора
.
Задание 16.
Линейный
оператор
![]() в базисе
в базисе
![]() имеет матрицу
имеет матрицу
![]() (
(![]() – ортонормированный базис). Найти
матрицу
– ортонормированный базис). Найти
матрицу
![]() сопряженного линейного оператора
сопряженного линейного оператора
![]() в базисе
.
Проверить справедливость равенства
в базисе
.
Проверить справедливость равенства
![]() .
.
16.1.
|
16.2.
|
16.3.
|
16.4.
|
16.5.
|
16.6.
|
16.7.
|
16.8.
|
16.9.
|
16.10.
|
16.11.
|
16.12.
|
16.13.
|
16.14.
|
16.15.
|
16.16.
|
16.17.
|
16.18.
|
16.19.
,
|
16.20.
|
Теорема Фредгольма, ее применение к исследованию слау
Рассмотрим неоднородную систему линейных алгебраических уравнений
![]() ,
(2.5)
,
(2.5)
где
,
![]() ,
,
![]() .
.
Система уравнений вида
![]() ,
(2.6)
,
(2.6)
где
![]() ,
,
![]() ,
,
![]() называется однородной
системой линейных алгебраических
уравнений, сопряженной к системе (2.5).
называется однородной
системой линейных алгебраических
уравнений, сопряженной к системе (2.5).
Теорема
Фредгольма.
Для того
чтобы система (2.5) была совместной,
необходимо и достаточно, чтобы
вектор-столбец
![]() был ортогонален ко всем решениям
сопряженной системы (2.6).
был ортогонален ко всем решениям
сопряженной системы (2.6).
Задание 17 (применение теоремы Фредгольма к исследованию СЛАУ). Используя теорему Фредгольма, исследовать систему

на совместность.
В ответе записать общее решение исходной
СЛАУ и сопряженной СЛАУ. Фактические
значения параметров
![]() для соответствующего варианта взять
из следующей таблицы:
для соответствующего варианта взять
из следующей таблицы:
№ вар. |
|
|
|
|
№ вар. |
|
|
|
|
1 |
2 |
2 |
3 |
4 |
11 |
3 |
4 |
4 |
2 |
2 |
2 |
4 |
3 |
1 |
12 |
3 |
2 |
4 |
1 |
3 |
3 |
2 |
1 |
4 |
13 |
2 |
3 |
4 |
3 |
4 |
4 |
1 |
2 |
3 |
14 |
4 |
4 |
2 |
1 |
5 |
2 |
4 |
1 |
3 |
15 |
2 |
2 |
4 |
3 |
6 |
2 |
1 |
3 |
2 |
16 |
2 |
2 |
3 |
4 |
7 |
1 |
3 |
4 |
2 |
17 |
4 |
2 |
2 |
2 |
8 |
2 |
3 |
1 |
2 |
18 |
1 |
4 |
3 |
2 |
9 |
2 |
3 |
1 |
4 |
19 |
4 |
1 |
2 |
3 |
10 |
3 |
2 |
1 |
4 |
20 |
2 |
4 |
2 |
2 |
Задание 18 (применение теоремы Фредгольма к исследованию СЛАУ). Дана система (фактические значения параметров взять из задания 17):

1. Используя теорему
Фредгольма, выяснить, при каком значении
параметра
![]() система совместна.
система совместна.
2. Провести исследование исходной системы, пользуясь теоремой Кронекера-Капелли. Показать, что СЛАУ будет совместна при найденном в пункте 1 значении параметра . Найти общее решение исходной СЛАУ.

 ,
,

 ,
,

 ,
,

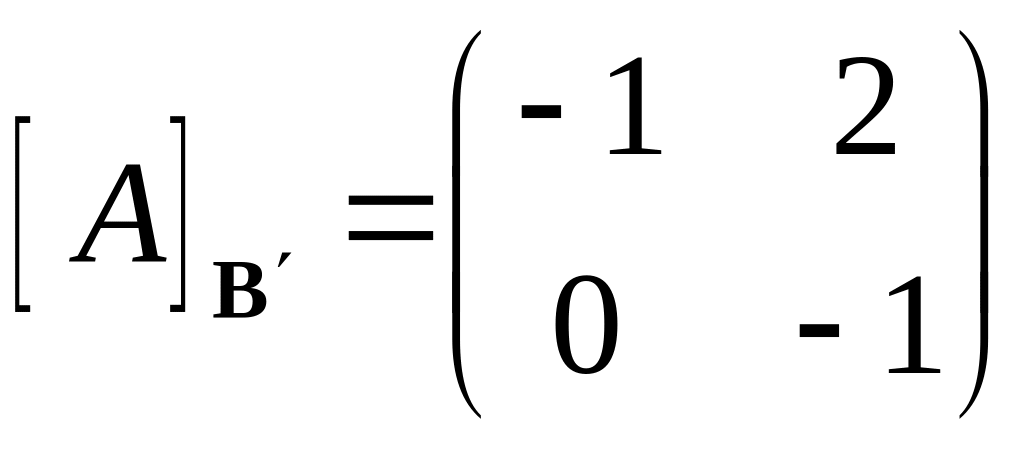 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,
 ,
,

 ,
,

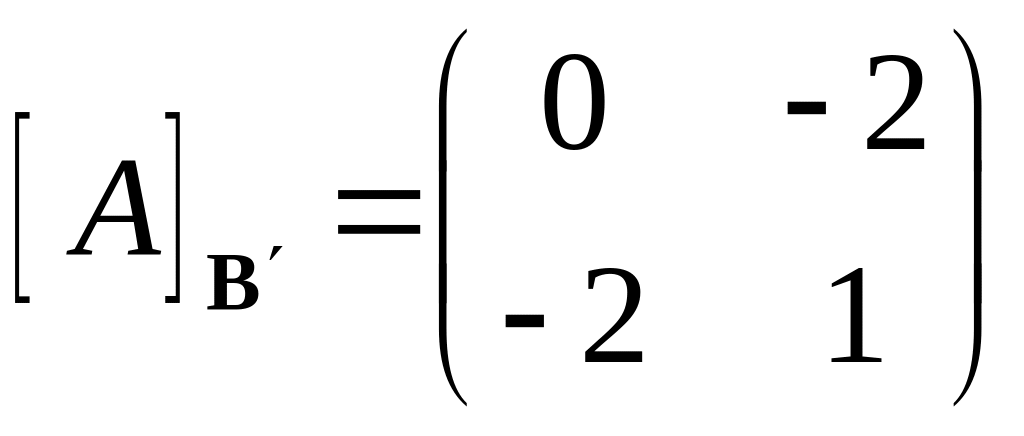 ,
,

 ,
,

 ,
,

 ,
,


 ,
,
