Вариант 2

Задание 1. Пусть система ненулевых векторов линейного пространства является линейно-зависимой. Какие из следующих высказываний истинные (верные):

а) существует вектор из системы векторов , который выражается в виде линейной комбинации через остальные векторы системы;

б) систему ненулевых векторов можно считать базисом в ;

в) система из векторов является линейно-зависимой;

г) система линейно-зависима.

(правильный ответ: а, в).

Задание 2. Размерность линейного пространства решений для системы равна:

а) 5; б) 2; в) 3; г) 4.

(правильный ответ: в).

Задание 3. В даны три вектора , , . Дополнение до базиса в предусматривает наличие в нем четвертого вектора:

а) ; б) ; в) ; г)

(правильный ответ: г).

Задание 4. Матрица перехода от к имеет вид . Связь между этими базисами описывается системой:

а) б) в) г)

(правильный ответ: а).

Задание 5. Пусть , базисы, причем связь между ними описывается равенствами . Формулы преобразования координат при переходе от к имеют вид

а) б) в) г)

(правильный ответ: в).

Задание 6. Пусть ­евклидово пространство размерности n. Какие из высказываний являются верными:

а) в всегда существует ортонормированный базис из векторов ;

б) любая ортогональная система векторов , не содержащая нулевого вектора, линейно-независима;

в) любой ортогональный базис можно преобразовать в ортонормированный;

г) любая ортогональная система векторов линейно-зависима.

(правильный ответ: а, б, в).

Задание 7. В даны векторы , . Дополнение этих векторов до ортогонального базиса в состоит из вектора:

а) ; б) ; в) ; г) .

(правильный ответ: г).

Задание 8. Ортонормированный базис имеет вид:

а) б) в) г)

(правильный ответ: в).

Задание 9. Линейный оператор переводит вектор в вектор . Тогда матрица этого оператора имеет вид:

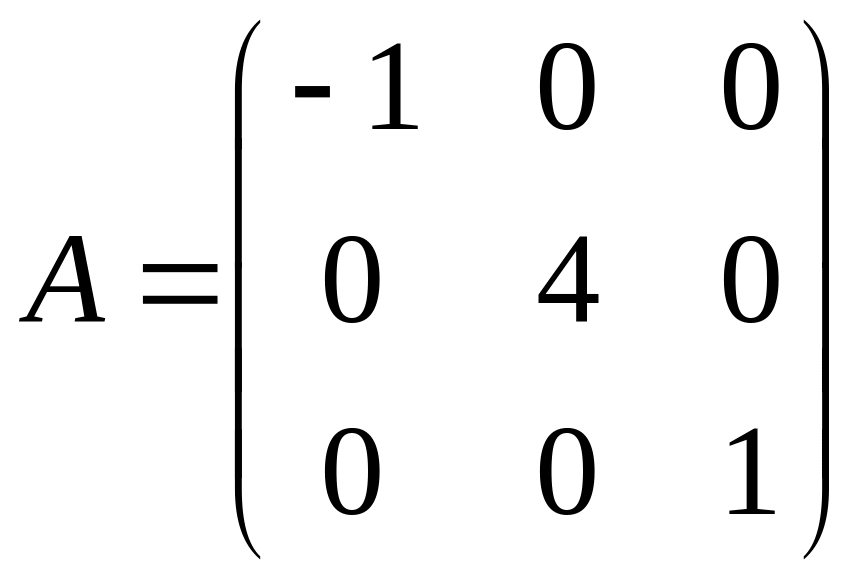а) ; б) ; в) ; г) .

(правильный ответ: а).

Задание 10. Линейный оператор определяется матрицей . Установить соответствие между понятиями для оператора.

(1) оператор является	( ) 1
(2) ранг оператора равен	( ) особенным (вырожденным)
(3) дефект оператора равен	( ) 2
(4) ядро оператора содержит вектор	( ) неособенным (невырожденным)
	( )
	( )

Правильный ответ

(1) оператор является	(3) 1
(2) ранг оператора равен	(1) особенным (вырожденным)
(3) дефект оператора равен	(2) 2
(4) ядро оператора содержит вектор	( ) неособенным (невырожденным)
	( )
	(4)

Задание 11. Пусть оператор в базисе задается матрицей . Тогда в базисе , он имеет матрицу:

а) ; б) ; в) ; г) .

(правильный ответ: г).

Задание 12. Оператор задается матрицей . Установить соответствие между собственными числами и собственными векторами оператора.

(1)	()
(2)	()
(3)	()

(правильный ответ

(1)	(1)
(2)	(3)
(3)	(2)

Задание 13. Квадратичная форма имеет вид

. Тогда матрица этой формы имеет вид:

а) ; б) ; в) ; г)

(правильный ответ: а).

Задание 14. Квадратичная форма имеет вид . Какие из следующих высказываний верные:

а) форма является невырожденной (неособенной);

б) форма является вырожденной (особенной);

в) форма является знакоположительной;

г) ранг формы равен 3;

д) форма является знакопеременной.

(правильный ответ: а, в, г).

Задание 15. Установить соответствие между квадратичными формами и их типами:

(1)	() отрицательно-определенная
(2)	() положительно-определенная
(3)	() знакопеременная
(4)	() неотрицательно-определенная

правильный ответ

(1)	(3) отрицательно-определенная
(2)	(1) положительно-определенная
(3)	(4) знакопеременная
(4)	(2) неотрицательно-определенная

Задание 16. Квадратичная форма с матрицей является положительно-определенной, если:

а) все главные миноры матрицы строго отрицательны;

б) все главные миноры матрицы строго положительны;

в) знаки главных миноров матрицы чередуются, начиная со знака минус;

г) все главные миноры матрицы строго неотрицательны.

(правильный ответ: б).