
Задание 3. Для функций, заданных параметрически, найти и .
 11.
11.
 21.
21.

 12.
12.
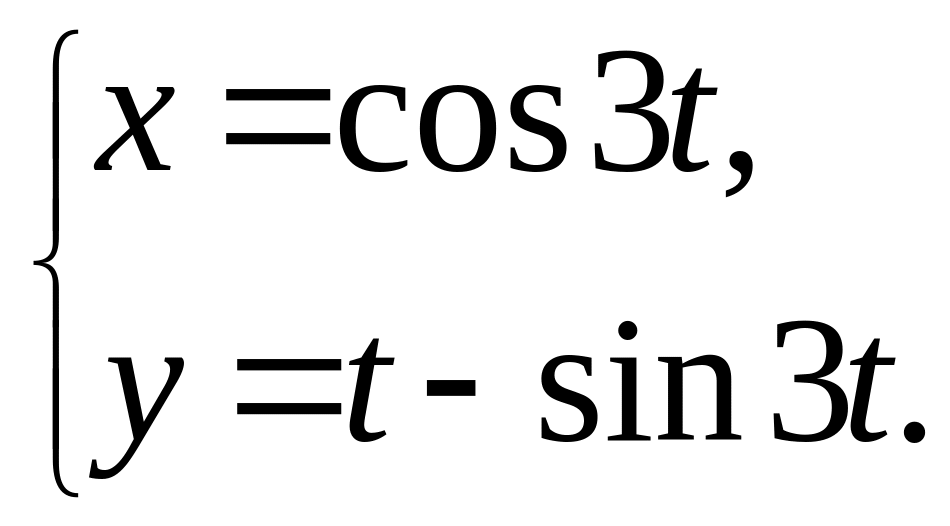 22.
22.

 13.
13.
 23.
23.

 14.
14.
 24.
24.

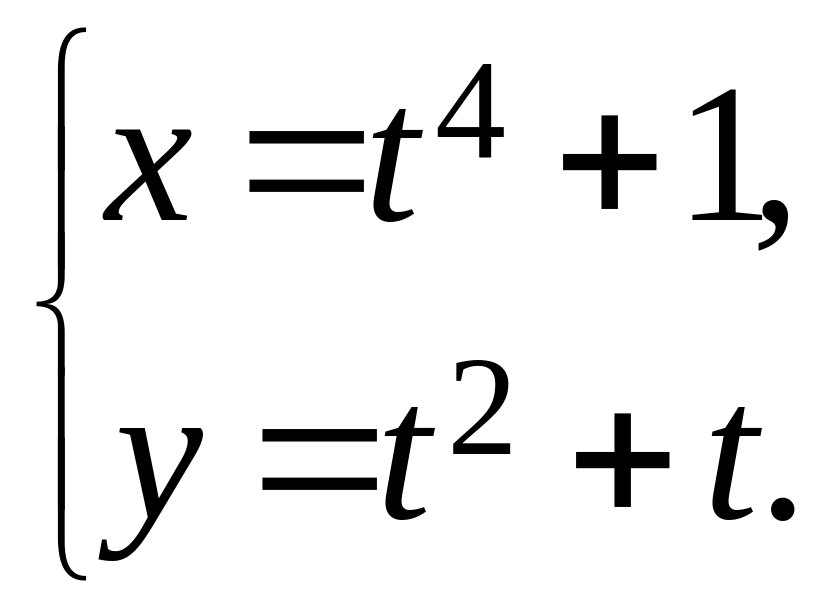 15.
15.
 25.
25.

 16.
16.
 26.
26.

 17.
17.
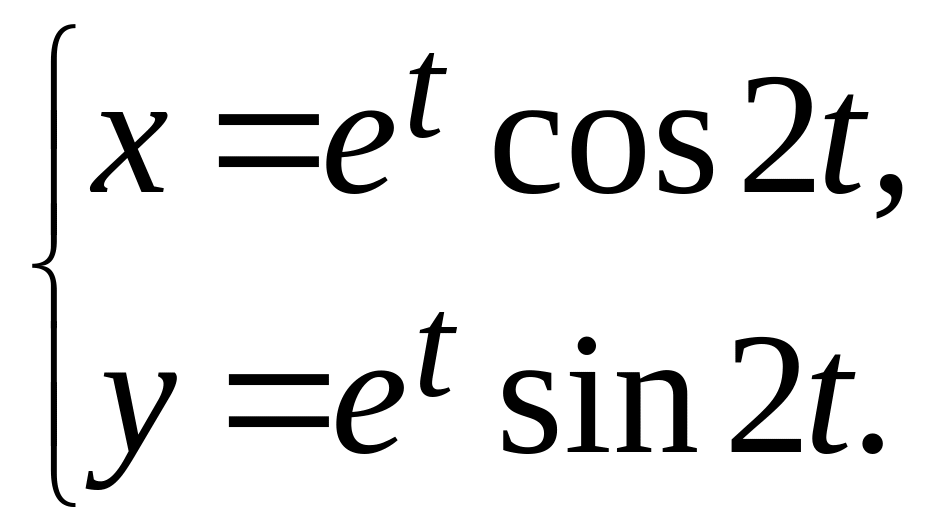 27.
27.
 18.
18.
 28.
28.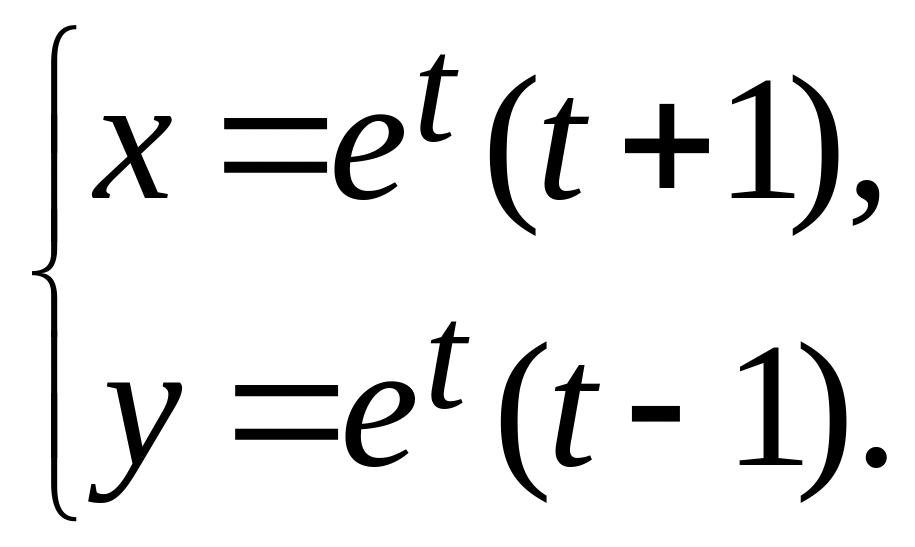
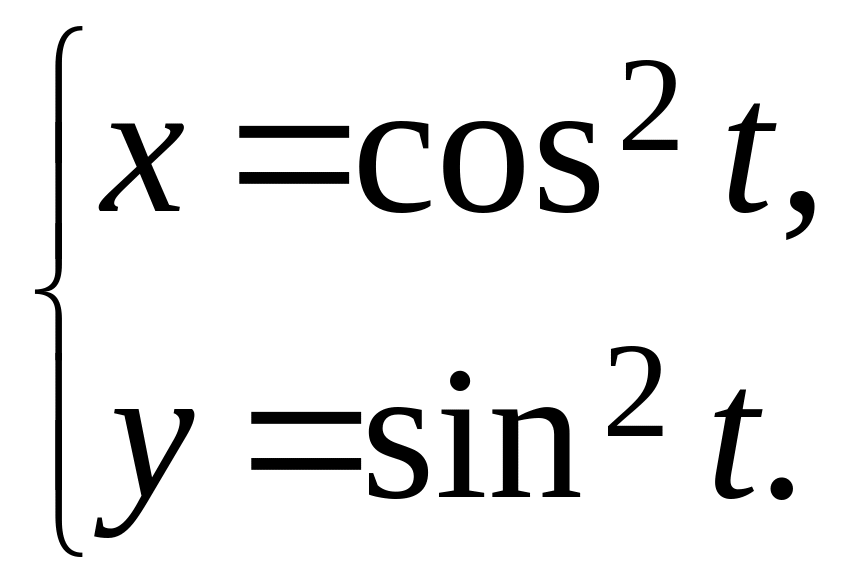 19.
19.
 29.
29.
 20.
20.
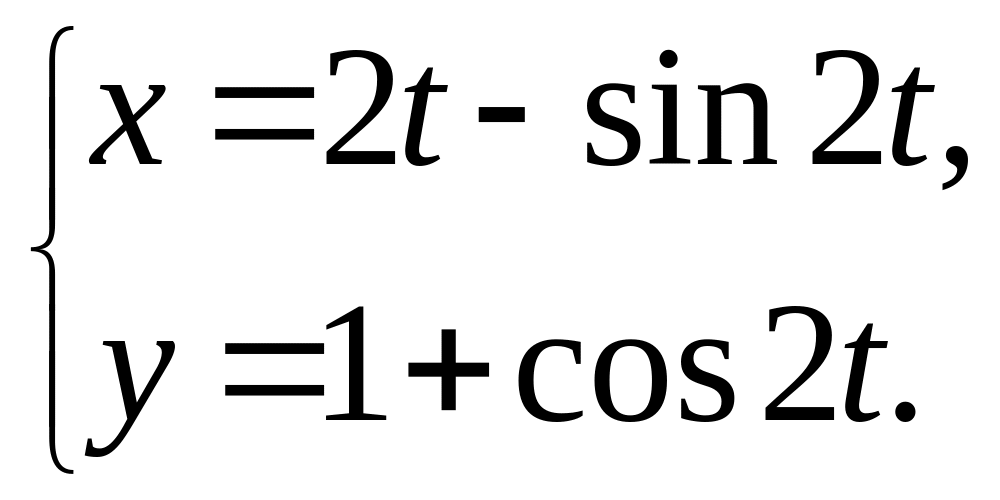 30.
30.
§4. Дифференцирование неявных функций
4.1.
Говорят,
что уравнение
![]() задает неявно
функцию
,
на интервале
задает неявно
функцию
,
на интервале
![]() ,
если для всех
,
если для всех
![]() выполняется равенство F
( x;
y
(x))
= 0.
выполняется равенство F
( x;
y
(x))
= 0.
Для
вычисления производной функции
![]() следует продифференцировать по
следует продифференцировать по
![]() тождество
тождество
![]() ,
помня, что
,
помня, что
![]() есть функция от x,
а затем полученное уравнение разрешить
относительно
есть функция от x,
а затем полученное уравнение разрешить
относительно
![]() .
.
4.2.Пример
1. Найти значение
![]() в точке
в точке
![]() для функции, заданной неявно уравнением
для функции, заданной неявно уравнением
![]() .
.
Решение. Дифференцируя по x обе части данного уравнения и считая при этом функцией от x, получаем:
![]() ,
,
откуда
![]() .
.
Полагая
x
= 1, y
= –1, находим
![]() .
.
4.3.Пример 2. Найти величину угла между касательными, проведенными в точках пересечения кривой x2 + y2 – 4 x + 4 y + 3 = 0 с осью Ox. Сделать чертеж.
Р е ш е н и е. Поступая по аналогии с предыдущим примером, находим:
y'
=![]() (*)
(*)
Точки пересечения данной кривой с прямой y = 0 являются решениями следующей системы:
![]()
Таких точек две: А(1;0) и В(3;0). Полагая x =1, y =0, находим согласно (*) угловой коэффициент k1 касательной к данной кривой в точке А:
k1
= у' (А ) =
![]() =
=![]() .
.
Аналогично находим угловой коэффициент k2 касательной в точке В:
k
2 = у'
(В
) =
![]() .
Угол θ
удовлетворяет равенству
,
значит
.
Угол θ
удовлетворяет равенству
,
значит
tg θ
=
![]() ,
откуда θ = arctg
(–
,
откуда θ = arctg
(–![]() )
126055'.
)
126055'.
Прежде
чем сделать чертеж , преобразуем данное
уравнение в уравнение (х – 2) 2
+ (у + 2) 2 = 5, которое определяет
окружность с центром О'(2;2) и радиусом
R=![]() ( рис.3).
( рис.3).

Рис.3
Задание 4. Найти значение в точке М(x0,y0) для функций, заданных неявно.
1. x3 – 2x2 y2 + 5x + y – 5 = 0, M (1; 1).
2. x2 + 2xy2 + 3y4 – 6 = 0, M (1; –1).
3. x4 – 6x2y2 + 9y2 – 5x2 + 15y2 + 4 = 0, M (2; 1).
4. x3 + y3 – 3xy + 1 = 0, M ( –2;1).
5. 5x2 + 3xy – 2y2 + 2 = 0, M (0; 1).
6. x2 + y2 – 4x – 10y + 19 = 0, M (3; 2).
7. x3 + x2y + y2 – 13 = 0, M (1; 3).
8. x3 – 2x2 + y2 = 0, M (1; 1).
9. x2 + 5xy + y2 – 2x + y – 6 = 0, M (1; 1).
10. x5 + y5 – 2xy = 0, M (1; 1).
11. x2 + xy + y2 = 7, M ( –1; –2).
12. 2x3 – xy + y – 2 = 0, M (1; 5).
13. 3x2 – xy + y – 3 = 0, M (1; –2).
14. x2 + 2y2 + 6x – 4y – 13 = 0, M (1; –1).
15. 3x2 – 5y2 – 6x – 20y + 25 = 0, M (2; 1).
16. 4x2 + y2 + 8x – 4y + 3 = 0, M (0; 1).
17. 2x2 – 9y2 + 4x + 18y + 11 = 0, M (2; –1).
18. x3 – xy + y + 7 = 0, M ( –1; –3).
19. x4 – y2 – y – 1 = 0, M (1; 0).
20. x3 + 2xy2 + y + 11 = 0, M ( –1; –2).
21. x3 + 5xy + y3 – 7 = 0, M (1; 1).
22. 3x2 – xy + y3 – x = 0, M (0; 2).
23. x 6 + y 6 – 2xy = 0, M (1; 1).
24. x 2 +x2 y – y2 – y = 0, M (1; 1).
25. 7x2 + xy – y3 + 3 = 0, M (1; –2).
26. x2y2 + xy + x2 – 7 = 0, M (1; 2).
27. 2x5 + y5 – 2xy + 26 = 0, M (1; –2).
28. 3x2 – xy + y 2 + x – 34 = 0, M ( –2; 4).
29. x2 – x2 y + y 2 = 13, M ( –1; –3).
30. x2 y2 – 4y3 – x = 4, M (0; –1).
Задание 5. Найти угол между касательными, проведенными в
точках пересечения кривой F ( x; y) = 0 c oсью Оx .Сделать чертеж.
1. x 2 + x 2 – 2x + 4y –3 = 0. 2. x 2 + y 2 + 4x – 4y + 3 = 0.
3. x 2 + y 2 + 2x – 2y – 4 = 0. 4. x 2 + y 2 – 4y – 4 = 0.
5. x 2+ y 2 + 2x + 2y –3 = 0. 6. x 2 + 6x + y 2 – 2y + 6 = 0.
7. x 2 + y 2 – 10 x+ 9 = 0. 8. x 2 + 10x+ y 2 – 6y +16 = 0.
9. x 2 + 4x + y 2 + 2y – 4 = 0. 10. x 2 + y 2 + 4x – 4 = 0.
11. x 2 + y 2 + 10x + 9 = 0. 12. x 2 – 6x + y 2 – 6y + 8 = 0.
13. x 2 + y 2 – 14x + 40 = 0. 14. x 2 + y 2 + 4x + 2y + 3 = 0.
15. x 2 + y 2 + 6x + 6y + 8 = 0. 16. x 2 + y 2 + 14x + 40 = 0.
17. x 2 + y 2 + 6x – 6y + 8 = 0. 18. x 2 + y 2 + 4x – 2y – 4 = 0.
19. x 2 + y 2 – 2x + 6y – 6 = 0. 20. x 2 + y 2 – 6x + 2y + 1 = 0.
21. x 2 + y 2 + 6x + 2y + 1 = 0. 22. x 2 + 6x + y 2 – 2y + 1 = 0.
23. x 2 + y 2 + 2x + 4y – 4 = 0. 24. x 2 + y 2 – 6x – 2y + 6 = 0.
25. x 2 + y 2 + 10x + 6y + 16 = 0. 26. x 2 + 4x + y 2 – 2y – 3 = 0.
27. x 2 + y 2 – 4x + 2y + 3 = 0. 28. x 2 + y 2 – 6x + 6y + 8 = 0.
29. x 2 + 4x + y 2 – 2y + 3 = 0. 30. x 2 + y 2 – 2x + 4y – 20 = 0.
