1. 3. Нахождение обратной матрицы.

Матрица называется обратной по отношению к матрице , если произведения и равны единичной матрице:

.

Пусть , тогда найдется по формуле:

,

где — определитель матрицы , а – алгебраическое дополнение элемента матрицы .

Если , обратная матрица не существует (не определяется).

Пример 2. Дана матрица . Найти ей обратную.

Решение. Вычисляем определитель матрицы:

.

Находим алгебраические дополнения элементов этого определителя:

, , ,

, , ,

, , .

Следовательно,

.

Проверка. Если обратная матрица найдена правильно, то должно выполняться равенство: .

.

1. 4. Решение систем линейных уравнений (СЛУ). Дана система трех линейных уравнений с тремя неизвестными:

Эту систему можно записать в матричном виде: , где

, , .

1. 4. 1. Метод Крамера для решения СЛУ. Если , то система имеет единственное решение и находится по формулам:

, , ,

где — определитель матрицы , а

, , .

1. 4. 2. Метод Гаусса для решения СЛУ.

Допустим, что (если , то изменим порядок уравнений, выбрав первым такое, в котором коэффициент при не равен нулю).

1 ШАГ. Делим уравнение (1) на ; умножим полученное уравнение на и вычтем его из (2); затем умножим на и вычтем из (3). В результате приходим к системе:

2 ШАГ. Делим уравнение (5) на , умножаем полученное уравнение на и вычитаем его из (6). В результате система преобразуется к так называемому ступенчатому виду:

Из преобразованной системы все неизвестные определяются последовательно, начиная с .

4. 3. Матричный метод решения СЛУ. Пусть дана система . Домножим обе части данного выражения на слева, т. е. , так как , а , то придем к уравнению вида . Это и будет решением СЛУ.

Пример 3. Решить систему уравнений тремя способами:

Решение.

1) Метод Крамера. Запишем матрицу и столбец свободных членов :

,

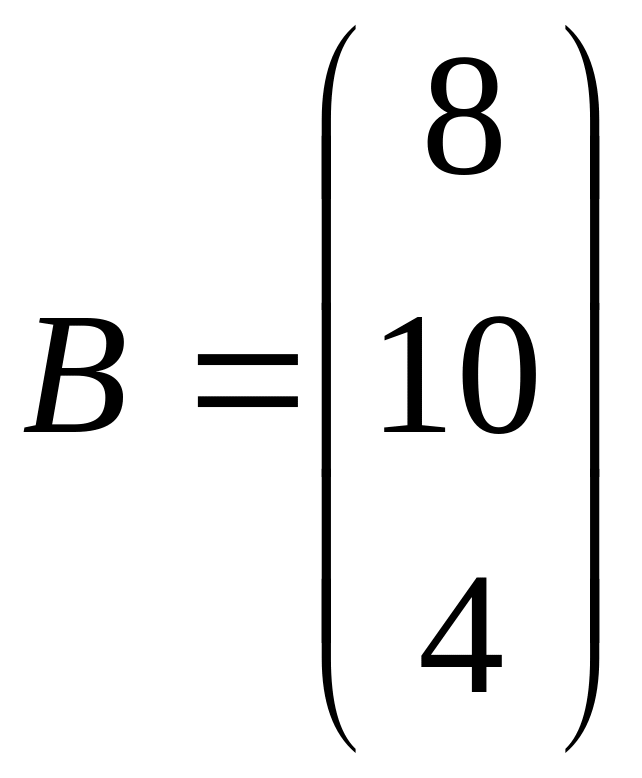
Решение данной системы найдем по формулам:

, , ,

где ,

,

,

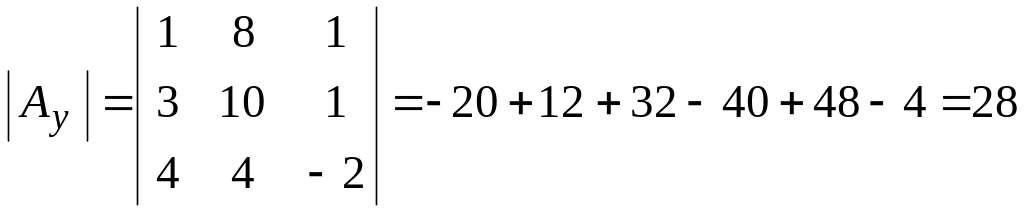Следовательно,

, , ,

2) Метод Гаусса.

Умножим уравнения (а) на 3 и вычтем полученное уравнение из (б); затем умножим уравнение (а) на 4 и вычтем из уравнения (в), в итоге получим:

Разделим уравнение (д) на (-4); умножим полученное уравнение на (-5) и вычтем его из уравнения (е), получим:

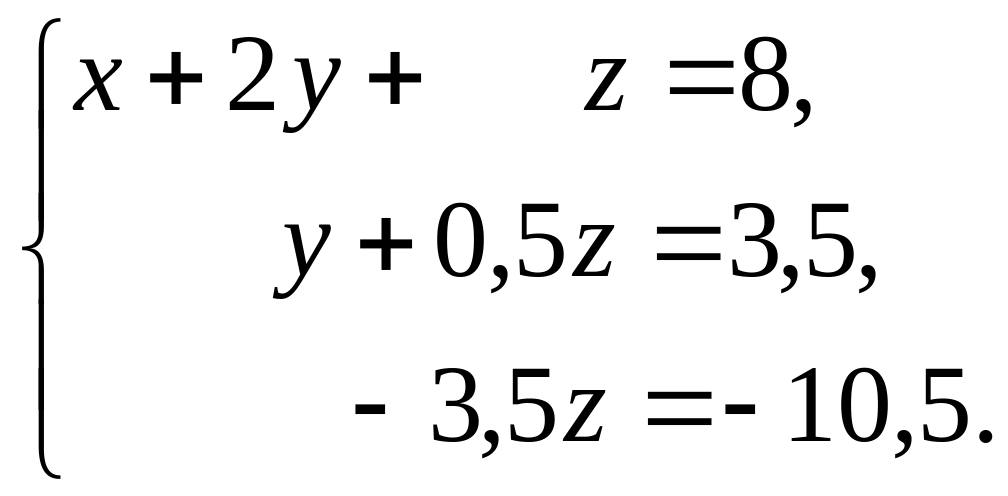
Из последнего уравнения находим ; далее, из второго

уравнения: ; из первого: .

Итого , , .

3) Матричный метод.

, .

Решение данной системы найдем по формуле .

Найдем . Определитель матрицы мы уже знаем . Вычислим алгебраические дополнения для элементов определителя матрицы А.

, , ,

, , ,

, , .

.

,

значит решением данной системы будет , , .