4.7. Алгоритм k – внутригрупповых средних

Рассмотрим компьютерную реализацию алгоритма K – внутригрупповых средних. Этот алгоритм наиболее часто используется в задачах распознавания образов. Он также используется для организации входных данных для нейронных сетей. Алгоритм, представленный ниже, минимизирует показатель качества, определенный как сумма квадратов расстояний всех точек, входящих в кластерную область, до центра кластера. Эта процедура, которую часто называют алгоритмом, основанным на вычислении К внутригрупповых средних, состоит из следующих шагов.

Шаг 1. Выбираются К исходных центров кластеров z₁(1), z₂(1), . . .,z_k(1). Этот выбор производится произвольно, и обычно в качестве исходных центров используются первые К результатов выборки из заданного множества образов.

Шаг 2. На k-м шаге итерации заданное множество образов {x} распределяется по К кластерам по правилу:

(4.3)

для всех i=1, 2, …,K, i≠j, где S_j(k) – множество образов, входящих в кластер с центром z_j(k). В случае равенства в (4.3) решение принимается произвольным образом.

Шаг 3. На основе результатов шага 2 определяются новые центры кластеров z_j(k+1), j=1, 2, …,К, исходя из условия, что сумма квадратов расстояний между всеми образами, принадлежащими множеству S_j(k), и новым центром кластера должна быть минимальной. Другими словами, новые центры кластеров z_j(k+1) выбираются таким образом, чтобы минимизировать показатель качества

. (4.4)

Центр z_j(k+1), обеспечивающий минимизацию показателя качества, является в сущности, выборочным средним, определенным по множеству S_j(k). Следовательно, новые центры кластеров определяются как

(4.5)

где N_j – число выборочных образов, входящих в множество S_j(k). Очевидно, что название алгоритма «К внутригрупповых средних» определяется способом, принятым для последовательной коррекции назначения центров кластеров.

Шаг 4. Равенство z_j(k+1)= z_j(k) при j=1, 2, …, К является условием сходимости алгоритма, и при его достижении выполнение алгоритма заканчивается. В противном случае алгоритм повторяется от шага 2.

Качество работы алгоритмов, основанных на вычислении К внутригрупповых средних, зависит от числа выбираемых центров кластеров, от выбора исходных центров кластеров, от последовательности осмотра образов и от геометрических особенностей данных. Хотя для этого алгоритма общее доказательство сходимости не известно, получение приемлемых результатов можно ожидать в тех случаях, когда данные образуют характерные гроздья, отстоящие друг от друга достаточно далеко. В большинстве случаев практическое применение этого алгоритма потребует проведения экспериментов, связанных с выбором различных значений параметра К и исходного расположения центров кластеров.

Компьютерный практикум № 2

Целью практикума является программная реализация алгоритма K – внутригрупповых средних для корректирования центров исходных классов. Классы составляют случайные величины с различными законами распределения.

Задачами практикума являются:

• формирование случайных величин с нормальным, равномерным и экспоненциальным законом распределения с использованием математического пакета Mathcad;

• определение основных характеристик распределения случайных величин по формулам, приведенным в компьютерном практикуме № 1;

• описание эталонных образов классов в виде векторов, характеристиками которых являются: математическое ожидание, дисперсия, среднеквадратическое отклонение, эксцесс и асимметрия законов распределения;

• применение алгоритма К– внутригрупповых средних для корректирования центров исходных классов случайных величин с рассмотренными законами распределения.

Реализация задания

В качестве примера представлен графический интерфейс программы, выполненной в среде Borland Delphi 7. Форма, предназначенная для реализации алгоритма К - внутригрупповых средних, показана на рис. 4.4.

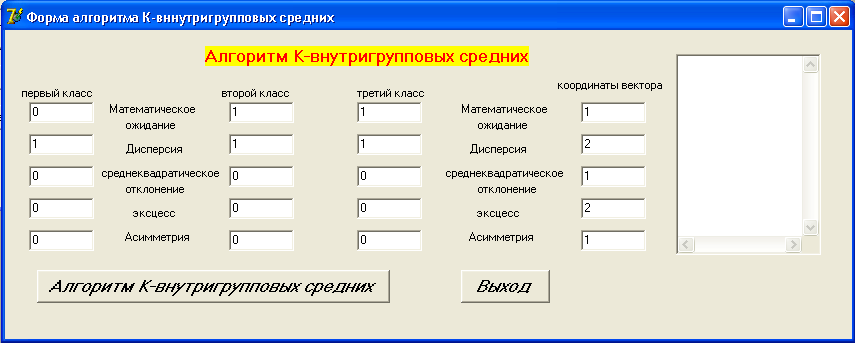
Рис. 4.4. Форма для алгоритма К– внутригрупповых средних

При запуске алгоритма выдается сообщение о том, что идет обработка введенного вектора (рис. 4.5).

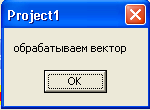
Рис. 4.5. Сообщения, выдаваемые при обработке вектора

После выполнения алгоритма в окне результатов будут выведены скорректированные центры исходных классов (рис. 4.6).

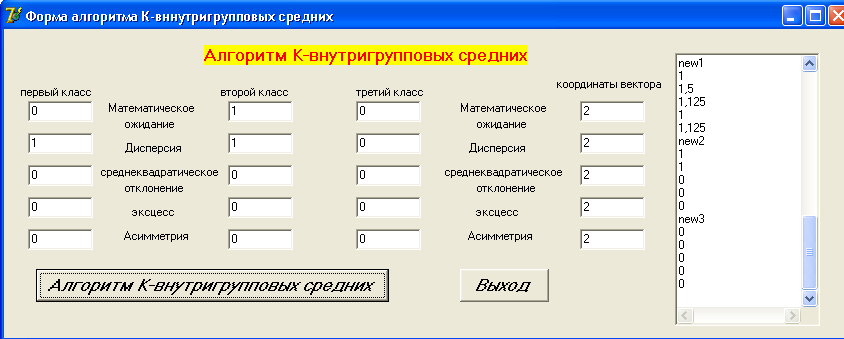
Рис. 4.6. Результат работы критерия

Задание для самостоятельной работы

Применить алгоритм К – внутригрупповых средних для корректирования центров исходных классов случайных величин с законами распределения: χ², Стьюдента, Фишера-Снедекора.